Diffusionskoeffizient

Der Diffusionskoeffizient , auch Diffusionskonstante oder Diffusivität genannt, dient in den Fickschen Gesetzen zur Berechnung des thermisch bedingten Transports eines Stoffes aufgrund der zufälligen Bewegung der Teilchen. Dabei kann es sich um einzelne Atome in einem Feststoff oder um Teilchen in einem Gas oder einer Flüssigkeit handeln. Der Diffusionskoeffizient ist daher ein Maß für die Beweglichkeit der Teilchen und lässt sich aus dem durchschnittlichen Quadrat der zurückgelegten Wegstrecke pro Zeit ermitteln.

Zur Angabe des Diffusionskoeffizienten gehört immer die Angabe, welcher Stoff in welchem Stoff diffundiert, sowie als wichtigste Einflussgröße die Temperatur. Die SI-Einheit des Diffusionskoeffizienten ist $\mathrm{m^2/s}$ .

Diffusionskoeffizienten in Gasen

Beispiele für Diffusionskoeffizienten in Gasen (bei 1 atm)
System	Temperatur in °C	Diffusionskoeffizient in m²s⁻¹
Luft – Sauerstoff	0	1,76 × 10⁻⁵
Luft – Kohlendioxid	8,9	1,48 × 10⁻⁵
Luft – Kohlendioxid	44,1	1,77 × 10⁻⁵
Wasserstoff - Stickstoff	24,1	7,79 × 10⁻⁵

Diffusionskoeffizienten in Gasen sind stark abhängig von Temperatur und Druck. In erster Näherung gilt, dass eine Verdopplung des Druckes zur Halbierung des Diffusionskoeffizienten führt.

Der Diffusionskoeffizient folgt gemäß der Chapman-Enskog-Theorie folgender Zahlenwertgleichung für zwei gasförmige Stoffe (Indizes 1 und 2):

$D = \frac{1{,}86 \cdot 10^{-3} \cdot T^{3/2} \sqrt{1/M_1 + 1/M_2}}{p \cdot \sigma_{12}^2 \cdot \Omega}$

mit

D – Diffusionskoeffizient (cm²/s)
T – Temperatur (K)
M – molare Masse (g/mol)
p – Druck (atm)
$\sigma_{12}=\frac{\sigma_1 + \sigma_2}{2}$ – (mittlerer) Kollisionsdurchmesser (Werte tabelliert) (Å)
Ω – Kollisionsintegral, abhängig von der Temperatur (Werte tabelliert) (−).

Für die Selbstdiffusion (d.h. für den Fall, dass nur eine Teilchensorte vorhanden ist) vereinfacht sich o.g. Zusammenhang zu:

$D = \frac{1}{3} \bar v \cdot l = \frac{2}{3} \frac{1}{n \cdot d^2} \sqrt{\frac{k_\mathrm{B} \cdot T}{\pi^3 \cdot m}}$

mit

$\bar v$ – mittlere thermische Geschwindigkeit der Teilchen (m·s⁻¹)
l – mittlere freie Weglänge (m)
n – Teilchenzahldichte (1/m³)
d – Teilchendurchmesser (m)
k_B – Boltzmann-Konstante (J·K⁻¹)
π – Pi
m - Molekülmasse (kg).

Empirische Näherungsformeln zur Berechnung von Diffusionskoeffizienten in Gasen finden sich in entsprechenden Standardwerken.

Diffusionskoeffizienten in Flüssigkeiten

Beispiele für Diffusionskoeffizienten in Wasser (bei unendlicher Verdünnung und 25 °C)
Stoff	Diffusionskoeffizient in m²s⁻¹
Sauerstoff	2,1 × 10⁻⁹
Schwefelsäure	1,73 × 10⁻⁹
Ethanol	0,84 × 10⁻⁹

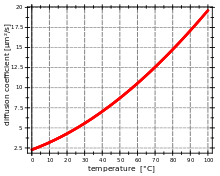
Temperaturabhängigkeit des Diffusionskoeffizienten von 100nm-Kügelchen (R₀=50nm) in Wasser

Diffusionskoeffizienten in Flüssigkeiten betragen in der Regel etwa ein Zehntausendstel von Diffusionskoeffizienten in Gasen. Sie werden beschrieben durch die Stokes-Einstein-Gleichung:

$D = \frac{k_\mathrm{B} \cdot T}{6 \cdot \pi \cdot \eta \cdot R_0}$

mit

k_B – Boltzmann-Konstante (J·K⁻¹)
T – Temperatur (K)
π – Pi
η – dynamische Viskosität des Lösungsmittels (in N·s·m⁻²)
R₀ – hydrodynamischer Radius der diffundierenden Teilchen (m)

Auf dieser Gleichung basieren viele empirische Korrelationen.

Da die Viskosität des Lösungsmittels eine Funktion der Temperatur ist, ist die Abhängigkeit des Diffusionskoeffizienten von der Temperatur nichtlinear.

Diffusionskoeffizienten in Feststoffen

Beispiele für Diffusionskoeffizienten in Feststoffen
System	Temperatur in °C	Diffusionskoeffizient in m²s⁻¹
Wasserstoff in Eisen	10	1,66 × 10⁻¹³
	50	11,4 × 10⁻¹³
	100	124 × 10⁻¹³
Kohlenstoff in Eisen	800	15 × 10⁻¹³
Kohlenstoff in Eisen	1100	450 × 10⁻¹³
Gold in Blei	285	0,46 × 10⁻¹³

Diffusionskoeffizienten in Feststoffen sind in der Regel mehrere tausend Mal kleiner als Diffusionskoeffizienten in Flüssigkeiten.

Für die Diffusion in Festkörpern sind Sprünge zwischen verschiedenen Gitterplätzen erforderlich. Dabei müssen die Teilchen eine Energiebarriere E überwinden, was bei höherer Temperatur leichter möglich ist als bei niedrigerer. Dies wird beschrieben durch den Zusammenhang:

$D = D_0 \cdot \exp\left(-\frac{E}{R \cdot T}\right)$

mit

E – Energiebarriere (in J·mol⁻¹)
R – allgemeine Gaskonstante (in J·K⁻¹mol⁻¹)
T – Temperatur (in K).

D₀ lässt sich näherungsweise berechnen als:

$D_0 \approx \alpha_0^2 \cdot N \cdot \omega$

mit

α₀ – Atomabstand (in m)
N – Anteil der vakanten Gitterplätze (ohne Einheit)
ω – Sprungfrequenz (in Hz)

Allerdings empfiehlt es sich, insbesondere Diffusionskoeffizienten in Feststoffen experimentell zu bestimmen.

Effektiver Diffusionskoeffizient

Der effektive Diffusionskoeffizient D_e beschreibt Diffusion durch den Porenraum poröser Medien. Da er nicht einzelne Poren, sondern den gesamten Porenraum betrachtet, ist er eine makroskopische Größe:

$D_e = \frac{\varepsilon_t \cdot \delta}{\tau} \cdot D$

mit

ε_t – Porosität, die für den Transport zur Verfügung steht; sie entspricht der Gesamtporosität abzüglich Poren, die aufgrund ihrer Größe für die diffundierenden Teilchen nicht zugänglich sind, und abzüglich Sackgassen- und blinder Poren (Poren ohne Verbindung zum restlichen Porensystem)
δ – Konstriktivität; sie beschreibt die Verlangsamung der Diffusion durch eine Erhöhung der Viskosität in engen Poren als Folge der größeren durchschnittlichen Nähe zur Porenwand und ist eine Funktion von Porendurchmesser und Größe der diffundierenden Teilchen.
τ – Tortuosität ("Gewundenheit")

Scheinbarer Diffusionskoeffizient

Der scheinbare (apparente) Diffusionskoeffizient erweitert den effektiven Diffusionskoeffizienten um den Einfluss der Sorption.

Für lineare Sorption berechnet er sich zu:

$D_a = \frac{D_e}{1 + \frac{K_d \cdot \rho}{\epsilon}}$

mit

K_d – linearer Sorptionskoeffizient (in m³·kg⁻¹)
ρ – Rohdichte (in kg·m⁻³)
ε – Porosität (ohne Einheit)

Bei nichtlinearer Sorptionsisotherme ist der scheinbare Diffusionskoeffizient stets eine Funktion der Konzentration, was die Berechnung der Diffusion erheblich erschwert.

Basierend auf einem Artikel in:

Wikipedia.de