
Tangens hyperbolicus und Kotangens hyperbolicus
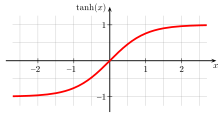

Tangens hyperbolicus und Kotangens hyperbolicus sind Hyperbelfunktionen. Man nennt sie auch Hyperbeltangens oder hyperbolischen Tangens bzw. Hyperbelkotangens oder hyperbolischen Kotangens.
Schreibweisen
| Tangens hyperbolicus: | |
| Kotangens hyperbolicus: |
Definitionen
Hierbei bezeichnen
und
den Sinus
hyperbolicus bzw. Kosinus
hyperbolicus.
Eigenschaften
| Tangens hyperbolicus | Kotangens hyperbolicus | |
|---|---|---|
| Definitionsbereich | ||
| Wertebereich | ||
| Periodizität | keine | keine |
| Monotonie | streng monoton steigend | |
| Symmetrien | Punktsymmetrie zum Koordinatenursprung | Punktsymmetrie zum Koordinatenursprung |
| Asymptoten | ||
| Nullstellen | keine | |
| Sprungstellen | keine | keine |
| Polstellen | keine | |
| Extrema | keine | keine |
| Wendepunkte | keine |
Spezielle Werte
Der Kotangens hyperbolicus hat zwei Fixpunkte, d.h., es gibt zwei ,
sodass
.
Sie liegen bei
(Folge
![]() A085984 in
OEIS)
A085984 in
OEIS)
Umkehrfunktionen
Der Tangens hyperbolicus ist eine Bijektion .
Die Umkehrfunktion
nennt man Areatangens
hyperbolicus. Sie ist für Zahlen x aus dem Intervall
definiert und nimmt als Wert alle reellen Zahlen an. Sie lässt sich durch den
natürlichen Logarithmus
ausdrücken:
Für die Umkehrung des Kotangens hyperbolicus gilt:
Ableitungen
Die -te
Ableitung ist gegeben durch
mit den Euler-Zahlen An,k.
Additionstheorem
Es gilt das Additionstheorem
analog dazu:
Integrale
Weitere Darstellungen
Reihenentwicklungen
Der Anfang der Taylorreihe des Tangens hyperbolicus lautet:
Die
sind die Bernoulli-Zahlen.
Der Konvergenzradius
dieser Reihe ist
.
Kettenbruchdarstellung
Johann Heinrich Lambert zeigte folgende Formel:
Numerische Berechnung
Grundsätzlich kann der Tangens hyperbolicus über die bekannte Formel
berechnet werden, wenn die Exponentialfunktion
zur Verfügung steht. Es gibt jedoch folgende Probleme:
- Große positive Operanden lösen einen Überlauf aus, obwohl das Endergebnis immer darstellbar ist
- Für Operanden nahe an 0 kommt es zu einer numerischen Auslöschung, womit das Ergebnis ungenau wird
Fall 1:
ist eine große positive Zahl mit
:
,
- wobei
die Anzahl der signifikanten Dezimalziffern des verwendeten Zahlentyps ist, was zum Beispiel beim 64-Bit-Gleitkommatyp double 16 ist.
Fall 2:
ist eine kleine negative Zahl mit
:
Fall 3:
ist nahe an 0, z. B. für
:
lässt sich hier über die Taylorreihe
sehr genau berechnen.
Fall 4: Alle übrigen :
Differentialgleichung
löst folgende Differentialgleichungen:
oder
mit
und
Komplexe Argumente
Anwendungen in der Physik
- Tangens und Kotangens hyperbolicus können benutzt werden, um die zeitliche
Abhängigkeit der Geschwindigkeit
beim Fall
mit Luftwiderstand oder auch beim Wurf nach unten zu beschreiben, wenn für
den Strömungswiderstand
eine turbulente
Strömung angesetzt wird (Newton-Reibung).
Das Koordinatensystem werde so gelegt, dass die Ortsachse nach oben zeigt. Für
die Geschwindigkeit gilt dann eine Differenzialgleichung der Form
mit der Schwerebeschleunigung g und einer Konstanten k > 0 mit der Einheit 1/m. Es gibt dann immer eine Grenzgeschwindigkeit
, die für
erreicht wird, und es gilt:
- beim Fall oder Wurf nach unten mit einer Anfangsgeschwindigkeit kleiner
der Grenzgeschwindigkeit:
mit
- beim Wurf nach unten mit einer Anfangsgeschwindigkeit größer der
Grenzgeschwindigkeit:
mit
- beim Fall oder Wurf nach unten mit einer Anfangsgeschwindigkeit kleiner
der Grenzgeschwindigkeit:
- In der Speziellen
Relativitätstheorie ist der Zusammenhang zwischen Geschwindigkeit v
und Rapidität
gegeben durch
mit der Lichtgeschwindigkeit c.
- Der Tangens hyperbolicus beschreibt ferner die thermische Besetzung eines
Zwei-Zustands-Systems in der Quantenmechanik:
Ist n die gesamte Besetzung der beiden Zustände und E ihr Energie-Unterschied, so
ergibt sich für die Differenz der Besetzungszahlen
, wobei
die Boltzmann-Konstante und T die absolute Temperatur ist.
- Wichtig für die Beschreibung der Magnetisierung eines Paramagneten ist die Brillouin-Funktion:
- Der Kotangens hyperbolicus tritt auch in der Kosmologie
auf: Die zeitliche Entwicklung des Hubble-Parameters
in einem flachen Universum, das im Wesentlichen nur Materie und Dunkle Energie enthält
(was ein gutes Modell für unser tatsächliches Universum ist), wird beschrieben
durch
, wobei
eine charakteristische Zeitskala ist und
der Grenzwert des Hubble-Parameters für
ist (
ist dabei der heutige Wert des Hubble-Parameters,
der Dichteparameter für die Dunkle Energie). (Dieses Ergebnis ergibt sich leicht aus dem zeitlichen Verhalten des Skalenparameters, das aus den Friedmann-Gleichungen abgeleitet werden kann.) Bei der Zeitabhängigkeit des Dichteparameters der Dunklen Energie tritt dagegen der Tangens hyperbolicus auf:
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 14.11. 2025