
Areatangens hyperbolicus und Areakotangens hyperbolicus
Areatangens hyperbolicus und Areakotangens hyperbolicus sind die Umkehrfunktionen von Tangens hyperbolicus und Kotangens hyperbolicus und damit Area-Funktionen.
Schreibweisen:
Letztere wird seltener benutzt, um die Verwechslung mit dem Kehrwert des
hyperbolischen (Ko-)Tangens zu vermeiden. Es ist .
Definitionen
Areatangens hyperbolicus:
Areakotangens hyperbolicus:
Geometrische Definitionen
Geometrisch lässt sich der Areatangens hyperbolicus durch die Fläche in der
Ebene darstellen, welche die Verbindungsstrecke zwischen dem Koordinatenursprung
und der Hyperbel
überstreicht: Es seien
und
Start- und Endpunkt auf der Hyperbel, dann wird von der Verbindungsstrecke die
Fläche
überstrichen.
Eigenschaften

Graph
der Funktion artanh(x) |
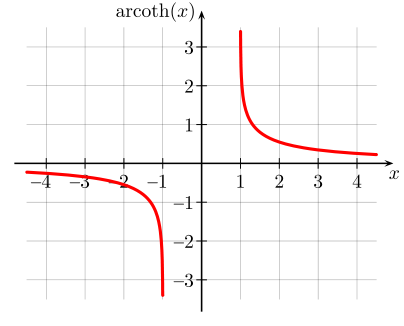
Graph
der Funktion arcoth(x) | |
| Areatangens hyperbolicus | Areakotangens hyperbolicus | |
|---|---|---|
| Definitionsbereich | ||
| Wertebereich | ||
| Periodizität | keine | keine |
| Monotonie | streng monoton steigend | keine |
| Symmetrien | ungerade Funktion: |
ungerade Funktion: |
| Asymptoten | ||
| Nullstellen | keine | |
| Sprungstellen | keine | keine |
| Polstellen | ||
| Extrema | keine | keine |
| Wendepunkte | keine |
Reihenentwicklungen
Taylor- und Laurent-Reihen der beiden Funktionen sind
Ableitungen
Integrale
Die Stammfunktionen lauten:
Additionstheoreme
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.02. 2020