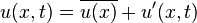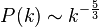Turbulente Strömung
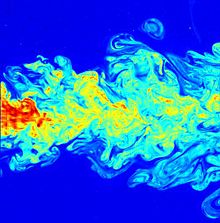
Die turbulente Strömung (lat. turbare = drehen, beunruhigen, verwirren) ist die Bewegung von Fluiden, bei der Verwirbelungen über einen weiten Bereich von Größenskalen auftreten. Diese Strömungsform ist gekennzeichnet durch ein meist dreidimensionales Strömungsfeld mit einer zeitlich und räumlich scheinbar zufällig variierenden Komponente. Den räumlichen Aspekt verdeutlicht nebenstehendes Bild, den zeitlichen z.B. das Rauschen des Windes.
Das Gegenteil ist die laminare Strömung.
Turbulenz führt zu verstärkter Durchmischung. Dies drückt sich aus in effektiv erhöhten Diffusionskoeffizienten. Bei großräumiger Turbulenz ist der Beitrag der molekularen Diffusion vernachlässigbar. Die Turbulenz transportiert nicht nur Stoffe (falls Konzentrationsunterschiede vorliegen), sondern auch andere physikalische Größen, wie innere Energie beim Wärmetransport oder Impuls. Der Druckverlust einer Rohrströmung beruht beispielsweise auf einer Diffusion von Impuls in Richtung Wand und ist bei turbulenter Strömung größer als bei laminarer Strömung. Gleichzeitig ist es der Geschwindigkeitsunterschied quer zur Strömung, in Abhängigkeit vom Abstand zur Wand, der die Turbulenz anregt. Mit steigendem Durchfluss durch ein Rohr nimmt daher die Intensität der Turbulenz zu und der Druckverlust steigt fast quadratisch an.
Eigenschaften
Turbulente Strömungen sind durch folgende Eigenschaften gekennzeichnet:
- ausgeprägte Selbstähnlichkeit („Skalierung“) bei Mittelwertbildung bezüglich Länge und Zeit, mit enorm großer Ausdehnung von zulässigen Längen- und Zeitskalen,
- ungeordnete und schwer vorhersagbare raumzeitliche Struktur,
- empfindliche Abhängigkeit von Anfangs-,
- empfindliche Abhängigkeit von Randbedingungen.
Beispiel zu (1): Ein Wirbelsturm ist mehrere Kilometer groß, während die kleinsten in ihm enthaltenen Wirbel kleiner als einen Millimeter sind.
Beispiel zu (2): Die Windgeschwindigkeit am Ort einer Windkraftanlage schwankt sehr stark und ist schwer vorhersagbar.
Beispiel zu (3): Die turbulente Strömung zwischen Strahl und Wand im Wandstrahl-Kippglied transportiert Impuls in den langsamen Teil der Grenzschicht, lässt ihn abströmen, was den Strahl an der Wand hält.
Beispiele zu (4): Schnee auf einer Tragfläche dämpft die großräumige Turbulenz in der Ablöseblase und führt zu Strömungsabriss schon bei geringeren Anstellwinkeln. Riblets auf Oberflächen können in turbulenter Strömung den Reibungswiderstand verringern, ebenso die Dimples genannten kleinen Vertiefungen auf der Oberfläche von Golfbällen.
Turbulenz (in Luftmassen, Fluiden) kann folgendermaßen definiert werden:
- Zufälligkeit (des Strömungszustandes, der Geschwindigkeiten): nicht vorhersagbar (oder praktisch nicht vorhersagbar, statistisch gesehen aber schon: siehe „deterministisches Chaos“)
- Diffusivität: starke und schnelle Durchmischung („Konvektion“, „Verwirbelung“), im Gegensatz zum Einfluss der langsameren molekularen Diffusion
- Dissipation: kinetische Energie wird auf allen Skalen fortgesetzt in Wärme umgewandelt und teilt sich aus den Skalen größerer Ausdehnung (größere „eddies“) in hierarchischer Weise in kleinere Elemente auf („Energiekaskade“, s.u.). Turbulenter Fluss bleibt also nur erhalten, wenn von außen Energie zugeführt wird.
- Nichtlinearität: der laminare Fluss wird instabil, wenn die Nichtlinearitäten an Einfluss gewinnen. Mit zunehmender Nichtlinearität kann eine Sequenz verschiedener Instabilitäten auftreten, bevor sich „volle Turbulenz“ ausbildet.
Entstehung
Zur Darstellung des Unterschiedes zwischen laminarer Strömung und turbulenter Strömung hat der Physiker Osborne Reynolds im Jahr 1883 einen Färbeversuch einer Wasserströmung in einer Rohrleitung vorgenommen und festgestellt, dass sich die Verwirbelung in der Rohrleitung erst ab einer Grenzgeschwindigkeit einstellen kann. Als Beurteilungskriterium wird hierzu die Reynolds-Zahl Re angewandt.

Die Lineare Stabilitätstheorie beschäftigt sich mit dem Umschlag – auch Transition – laminarer Strömungen in turbulente Strömungen. Sie betrachtet dazu das Anwachsen wellenförmiger Störungen mit kleiner Amplitude, d.h. das Anwachsen der Tollmien-Schlichting-Wellen aufgrund der Kelvin-Helmholtz-Instabilität.
Turbulenz kann auch durch spezielle Formgebung bewirkt werden, etwa in statischen Mischern oder durch die Dimples genannten kleinen Vertiefungen auf der Oberfläche von Golfbällen.
Beschreibung
Um turbulente Strömungen zu beschreiben, zerlegt man die Eigenschaftskomponenten wie die Geschwindigkeit und den Druck in einen gemittelten Term, der von einer statistischen Störbewegung überlagert wird (Reynoldsche Zerlegung):
Dabei handelt es sich bei der gemittelten Größe 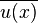 um den Ensembl-Mittelwert.
um den Ensembl-Mittelwert.
Setzt man diese Zerlegung in die Navier-Stokes-Gleichungen
ein, so erhält man zu Beschreibung von turbulenten Strömungen die Reynolds-Gleichungen,
die allerdings die Reynoldsspannungen als zusätzliche Unbekannte enthalten. Da
man nun mehr Unbekannte als Gleichungen hat, werden Schließungsansätze
benötigt, um das System zu lösen. Dabei haben unterschiedliche
Schließungsansätze (z.B. der Ansatz von Boussinesq und die
Prandtlsche
Mischungsweghypothese) zu verschiedenen Turbulenzmodellen
geführt (z.B. zum 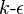 -Turbulenzmodell
und zur Large
Eddy Simulation).
-Turbulenzmodell
und zur Large
Eddy Simulation).
Turbulente Strömungen kann man in isotrope Turbulenz, homogene Turbulenz und Scherturbulenz klassifizieren, die jeweils bestimmte charakteristische Merkmale aufweisen. Da turbulente Strömungen mathematisch schwierig zu beschreiben sind, bezieht man sich zu ihrer Charakterisierung häufig auf die idealisierte Strömungsformen isotrope und homogene Turbulenz, da sich in diesen Fällen die Reynoldsgleichungen weiter vereinfachen. In der Praxis tritt oft die Scherturbulenz auf, z.B. in der Grenzschicht an der Oberfläche stromlinienförmiger Körper.
Wie schwierig, vielfältig und wenig verstanden die Turbulenz ist, zeigt folgendes Zitat:
„Wenn ich in den Himmel kommen sollte, erhoffe ich Aufklärung über zwei Dinge: Quantenelektrodynamik und Turbulenz. Was den ersten Wunsch betrifft, bin ich ziemlich zuversichtlich.“
Energiekaskade
Lewis Fry Richardson legte 1922 die Grundlage für die weitere Turbulenzforschung, indem er die heutige Vorstellung dieses Phänomens begründete. Nach seiner wegweisenden Interpretation wird bei einer turbulenten Strömung die Energie auf großer Skala zugeführt, durch den Zerfall von Wirbeln durch alle Skalen hindurch transportiert (sog. Inertialbereich) und bei kleinsten Skalen in Wärme dissipiert. Dies wird als Energiekaskade bezeichnet.
Die Theorie der Turbulenz wurde von Andrei
Nikolajewitsch Kolmogorow in seinen Arbeiten von 1941 und 1962
wesentlich vorangetrieben, als er das Skalenargument von Richardson durch eine
Ähnlichkeitshypothese
statistisch auswerten und damit für den Inertialbereich das
Kolmogorov-5/3-Gesetz herleiten konnte. Nach diesem hängt die spektrale
Leistungsdichte 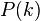 mit einem Exponenten von −5⁄3
von der Kreiswellenzahl k
ab:
mit einem Exponenten von −5⁄3
von der Kreiswellenzahl k
ab:
Auch der dissipative Bereich ist nach Kolmogorow benannt und wird als Mikroskala von Kolmogorow bezeichnet.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 04.04. 2023