
Hyperrechteck
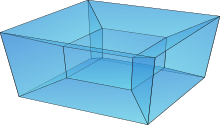
Ein Hyperrechteck oder auch Hyperquader ist in der Geometrie die Verallgemeinerung des Rechtecks und des Quaders auf beliebig viele Dimensionen. Der Hyperwürfel ist ein Spezialfall davon.
Definition
Ein achsenparalleles Hyperrechteck
im
-dimensionalen
Raum
ist das kartesische
Produkt von
reellen Intervallen
mit
für
,
das heißt
.
Im Allgemeinen ist ein Hyperrechteck eine Figur, die kongruent ist mit einem achsenparallelen Hyperrechteck.
Beispiele
Für
erhält man so ein Intervall, für
ein Rechteck und für
einen Quader.
Für den Spezialfall, dass alle Intervalle gleich dem Einheitsintervall
sind, erhält man den Einheitshyperwürfel
.
Eigenschaften
Begrenzende Elemente
Jedes -dimensionale
Hyperrechteck mit
hat
Ecken,
Kanten, die rechtwinklig aufeinanderstoßen, und
Seitenflächen, die ihrerseits Hyperrechtecke der Dimension
sind.
Allgemein wird ein -dimensionales
Hyperrechteck von
Hyperrechtecken der Dimension
begrenzt, wobei
ist.
Volumen und Oberfläche
Das Volumen eines Hyperrechtecks
beträgt
.
Das ist der Ausgangspunkt für die Volumenbestimmung sehr viel allgemeinerer
Mengen, wie in der Konstruktion des -dimensionalen
Lebesguemaßes
in der Maßtheorie
deutlich wird. Der Oberflächeninhalt
beträgt
.
Siehe auch
- Hyperwürfel - Spezialisierung für gleiche Kantenlängen
- Hilbertwürfel für den unendlichdimensionalen Fall
- Hyperebene
- Hyperraum


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.11. 2022