
Sekantenverfahren
Bei dem Sekantenverfahren handelt es sich um ein schon seit dem Mittelalter bekanntes numerisches
Verfahren zur näherungsweisen Lösung einer Gleichung
des Typs .
Es entspricht einer Vereinfachung des Newton-Verfahrens,
da nicht die Ableitung der Funktion berechnet werden muss.
Verfahren
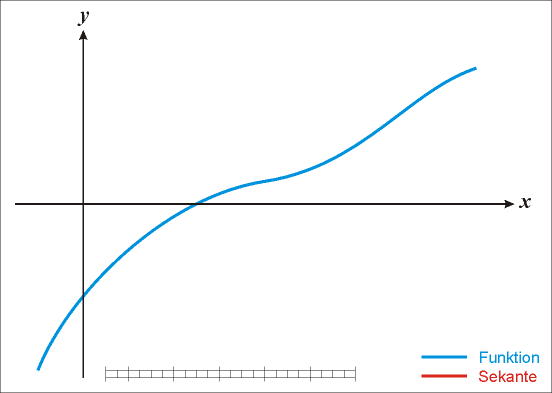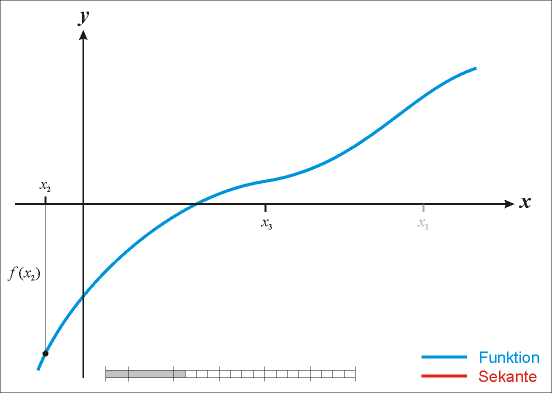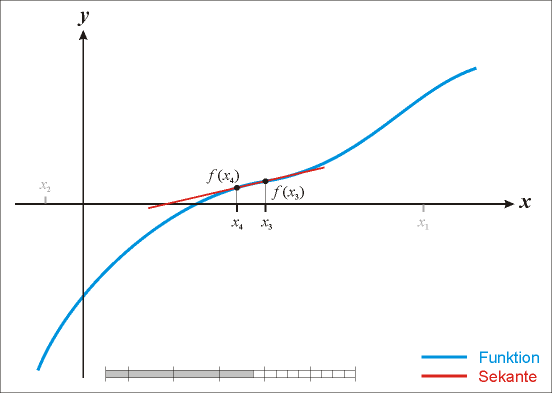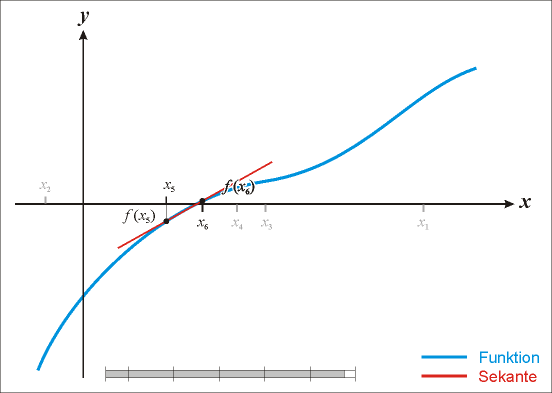
Zwischen zwei Punkten
und
der Funktion
wird eine Sekante gelegt. Der
Schnittpunkt der Sekante mit der
-Achse
wird als verbesserter Startwert
für die Iteration verwendet. Mithilfe
von
wird der neue Funktionswert
berechnet. Mit
und dem alten Wert
wird dieser Schritt wiederholt und erneut eine Sekante angelegt. Man wiederholt
diesen Schritt so lange, bis eine ausreichende Näherung der gesuchten Nullstelle
erreicht wurde.
Konstruktion am Graphen
Die folgende Animation zeigt, wie mit den Startwerten
und
weitere Punkte konstruiert werden.
Das Verfahren verwendet folgende Iterationsvorschrift:
Dabei wird mit zwei Näherungswerten
begonnen.
Im Gegensatz zum Regula-falsi-Verfahren
kann es beim Sekantenverfahren auftreten, dass die Nullstelle für einige
Iterationsschritte nicht mehr zwischen
und
liegt.
Zusammenhang mit dem Newton-Verfahren
Das Verfahren lässt sich als Modifikation des Newtonschen Näherungsverfahrens mit der Iterationsvorschrift
auffassen, indem man die Ableitung
durch den Differenzenquotienten
ersetzt.
Konvergenz
Aufgrund der Verwandtschaft mit dem Newtonschen Verfahren gelten für die Konvergenz des Sekantenverfahrens ähnliche Bedingungen:
- Das Sekantenverfahren konvergiert
superlinear mit der Konvergenzordnung
(dies entspricht dem Verhältnis des goldenen Schnittes), d.h. die Zahl der korrekten Stellen des Näherungswertes erhöht sich pro Durchgang ungefähr um den Faktor
. Dies hängt damit zusammen, dass der Differenzenquotient nur eine Näherung für die Ableitung ist; entsprechend geringer ist die Konvergenzgeschwindigkeit im Vergleich zum quadratisch konvergenten Newton-Verfahren.
- Die Funktion
muss im Definitionsbereich stetig verlaufen und genau eine Nullstelle besitzen.
- Das Verfahren verliert an Genauigkeit und Konvergenzgeschwindigkeit, wenn
die Ableitung
an der Nullstelle 0 wird, da sich in der Berechnung ein Ausdruck der Form
ergibt. Speziell bei Polynomen entspricht dies einer mehrfachen Nullstelle.
- Bei der numerischen Berechnung stellt sich das Problem, dass der Differenzenquotient
- mit zunehmender Annäherung an die Nullstelle durch Auslöschung der Ziffern in die Form 0/0 übergeht. Während das Verfahren selbst die Abschätzung für die Nullstelle immer weiter verbessern könnte, wird in der tatsächlichen Berechnung dieser Gewinn in der Nähe der Nullstelle durch zunehmende Rundungsfehler überkompensiert. Dadurch lässt sich auf Rechnern mit endlicher Stellenzahl prinzipiell mit dem Sekantenverfahren nicht die Genauigkeit des Newtonschen Verfahrens erreichen.
Vorteile des Verfahrens
Gegenüber dem Newtonschen Verfahren ergeben sich mehrere Vorteile:
- Es müssen nur die Funktionswerte berechnet werden. Im Gegensatz zur Newton-Iteration können damit die Nullstellen jeder beliebigen, hinreichend glatten Funktion auch ohne Kenntnis oder Berechnung der Ableitungen berechnet werden.
- Je Iterationsschritt muss nur der Funktionswert
einmal berechnet werden. Beim Newtonverfahren muss zusätzlich auch noch der Funktionswert der Ableitung
bestimmt werden.
- Durch die Vorgabe von zwei Startwerten lässt sich das Verfahren besser auf ein bestimmtes Intervall fokussieren, da die Richtung der Sekante durch die beiden Startwerte vorgegeben wird. Die Konvergenz kann dadurch allerdings nicht erzwungen werden.
Das Sekantenverfahren im Mehrdimensionalen
Analog zum mehrdimensionalen
Newton-Verfahren kann man auch ein mehrdimensionales Sekantenverfahren
definieren, um Nullstellen von Funktionen
zu bestimmen.
Wurde im Eindimensionalen die Ableitung durch den Differenzenquotient approximiert, so wird im Mehrdimensionalen die Jacobi-Matrix approximiert:
,
wobei
zu einer gegebenen Schrittweitenmatrix
definiert ist durch:
, sofern
ist.
Nun ergibt sich analog zum Newtonverfahren folgende Iterationsvorschrift:
Da das Lösen von
über die Berechnung der Inversen
einer Matrix und anschließender Multiplikation mit
aufwändiger und numerisch ungünstiger ist, wird stattdessen das lineare
Gleichungssystem
gelöst. Danach erhält man
aus:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.11. 2019