Heron-Verfahren

Das Heron-Verfahren, Heronsche Näherungsverfahren oder babylonische Wurzelziehen ist ein Rechenverfahren zur Berechnung einer Näherung der Quadratwurzel einer reellen Zahl a>0 .

Verfahren

Heron-Verfahren zur Berechnung von ${\sqrt {2}}$ mit drei verschiedenen Startwerten

Die Iterationsgleichung des Heron-Verfahrens kann aus dem Newton-Verfahren für die Nullstelle der quadratischen Funktion $f(x)=x^{2}-a$ hergeleitet werden. Mit f'(x)=2x folgt aus der Rekursionsformel des Newton-Verfahrens $x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}$ die Iterationsvorschrift:

$x_{n+1}=x_{n}-{\frac {x_{n}^{2}-a}{2x_{n}}}={\frac {x_{n}^{2}+a}{2x_{n}}}={\frac {1}{2}}\cdot \left(x_{n}+{\frac {a}{x_{n}}}\right)$ .

Der Startwert $x_{0}$ der Iteration kann, solange er nicht gleich Null ist, beliebig festgesetzt werden, die Iteration konvergiert immer. Zu beachten ist, dass bei negativen Startwerten die Iteration gegen die negative Quadratwurzel konvergiert. Eine qualifizierte Schätzung für den Startwert erhält man aus der Taylorreihen-Entwicklung der binomischen Reihe um 1, deren zwei erste Glieder diese Gleichung liefern: $x_{0}={\tfrac {a+1}{2}}$

Das Heron-Verfahren gehört zu den Fixpunktverfahren. Setzt man ${\textstyle \varphi (x)={\frac {1}{2}}\cdot \left(x+{\frac {a}{x}}\right)}$ , so gilt für den Fixpunkt (der die Bedingung ${\textstyle \varphi (x)=x}$ erfüllt) ${\textstyle x^{2}=a}$ mit der (positiven) Lösung ${\textstyle x={\sqrt {a}}}$ .

Beispiel

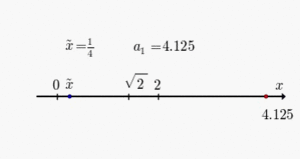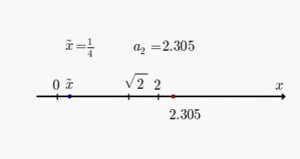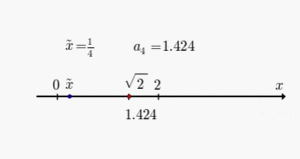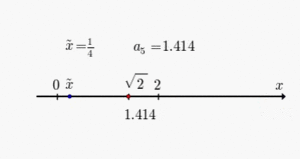
Die Folgenglieder der babylonischen Wurzelfolge mit dem Startwert $a_{0}={\tfrac {1}{4}}$ .

Im folgenden einfachen Beispiel wird die Wurzel aus 9 als Annäherung mit drei Berechnungsschritten an den wahren Wert $\textstyle {\sqrt {9}}=3$ gezeigt. Mit $\textstyle a=9$ wird der Startwert $\textstyle x_{0}={\frac {9+1}{2}}=5$ für die Iteration berechnet und in die Iterationsvorschrift eingesetzt:

$x_{1}={\frac {1}{2}}\cdot \left(5+{\frac {9}{5}}\right)={\frac {1}{2}}\cdot {\frac {34}{5}}={\frac {34}{10}}=3{,}4$

$x_{2}={\frac {1}{2}}\cdot \left({\frac {34}{10}}+{\frac {9}{\frac {34}{10}}}\right)={\frac {1}{2}}\cdot \left({\frac {34}{10}}+{\frac {90}{34}}\right)={\frac {257}{85}}=3{,}0235294\dots$

$x_{3}={\frac {1}{2}}\cdot \left({\frac {257}{85}}+{\frac {9}{\frac {257}{85}}}\right)={\frac {1}{2}}\cdot \left({\frac {257}{85}}+{\frac {765}{257}}\right)={\frac {65537}{21845}}=3{,}000091554\dots .$

Konvergenz

Das Verfahren lässt sich folgendermaßen als rekursiv definierte Folge ausdrücken:

$x_{n+1}={\frac {1}{2}}\cdot \left(x_{n}+{\frac {a}{x_{n}}}\right)$ .

Es handelt sich dabei um eine rein positive Folge. Man kann nun zeigen, dass für alle $n\geq 1$ das -te Folgenglied $x_{n}\geq {\sqrt {a}}$ ist. Dazu zeigt man die äquivalente Ungleichung $x_{n}^{2}-a\geq 0$ :

$x_{n}^{2}-a={\frac {1}{4}}\cdot \left(x_{n-1}+{\frac {a}{x_{n-1}}}\right)^{2}-a={\frac {1}{4}}\cdot \left(x_{n-1}-{\frac {a}{x_{n-1}}}\right)^{2}\geq 0$ .

Weiter zeigt man, dass $\left(x_n\right)$ eine monoton fallende Folge ist:

$x_{n+1}-x_{n}={\frac {1}{2}}\cdot \left(x_{n}+{\frac {a}{x_{n}}}\right)-x_{n}={\frac {a}{2x_{n}}}-{\frac {x_{n}}{2}}={\frac {a-x_{n}^{2}}{2x_{n}}}\leq 0$ .

Durch die gezeigte Beschränktheit und Monotonie muss die Folge konvergieren, und zwar von oben gegen die gesuchte Wurzel:

$x={\frac {1}{2}}\cdot \left(x+{\frac {a}{x}}\right)\Leftrightarrow x^{2}=a\Leftrightarrow x={\sqrt {a}}$ .

Da sich das Heron-Verfahren aus dem Newtonschen Näherungsverfahren ableiten lässt und die zu berechnende Nullstelle einfach ist, ist die Konvergenzordnung 2.

Das Verfahren konvergiert sehr schnell, wenn bereits eine gute Näherung vorliegt. Die Zahl der richtigen Stellen wird mit jedem Schritt etwa verdoppelt. Wenn die erste Näherung jedoch schlecht ist, sind viele Schritte für eine gute Näherung nötig.

Wenn zum Beispiel aus einer Ganzzahl mit 200 Binärstellen die Wurzel berechnet werden soll und man mit $x_{0}=a$ als erster Näherung beginnt, dann wird die Näherung mit jedem Schritt um etwa eine Binärstelle kürzer, d.h. erst nach etwa 100 Schritten hat die Näherung die richtige Länge von 100 Stellen. Danach reichen sechs bis sieben weitere Schritte ( $\log _{2}(100)$ ), um alle 100 Stellen vor dem Komma richtig zu berechnen.

Es empfiehlt sich somit, einen möglichst genauen Startwert $x_{0}$ zu bestimmen. Im Beispiel sollte man zuerst die Bitlänge $\lfloor \log _{2}(a)\rfloor +1$ von ermitteln und einen Startwert mit der halben Länge verwenden.^{[Anmerkung
1]}

Fehlerabschätzung

Für die Heron-Folge $(x_{n})_{n\geq 1}$ gilt:

${\frac {a}{x_{n}}}\leq {\sqrt {a}}\leq x_{n}$ (Einschließung),

und für den Fehler die folgende Abschätzung

$x_{n}-{\sqrt {a}}={\frac {1}{2x_{n-1}}}\left(x_{n-1}-{\sqrt {a}}\right)^{2}\leq {\frac {1}{2{\sqrt {a}}}}\left(x_{n-1}-{\sqrt {a}}\right)^{2}$ (quadratische Konvergenz).

Diese Fehlerabschätzung hat den Nachteil, dass ${\sqrt {a}}$ nicht bekannt ist, sondern berechnet werden soll. Unter Verwendung der obigen Einschließung erhält man folgende praktikable Abschätzung:

$x_{n}-{\sqrt {a}}={\frac {1}{2x_{n-1}}}\left(x_{n-1}-{\sqrt {a}}\right)^{2}\leq {\frac {1}{2x_{n-1}}}\left(x_{n-1}-{\frac {a}{x_{n}}}\right)^{2}={\frac {1}{2x_{n-1}\cdot x_{n}^{2}}}\left(x_{n-1}\cdot x_{n}-a\right)^{2}$ .

Angewandt auf obiges Beispiel erhält man:

$x_{3}-3={\frac {1}{2x_{2}}}\left(x_{2}-3\right)^{2}=0{,}000091554\dots \leq {\frac {1}{2x_{2}\cdot x_{3}^{2}}}\left(x_{2}\cdot x_{3}-9\right)^{2}=0{,}0000922\dots$ .

Für den relativen Fehler

$\varepsilon _{n}={\frac {x_{n}-{\sqrt {a}}}{\sqrt {a}}}$

gilt die Rekursion

$\varepsilon _{n+1}={\frac {\varepsilon _{n}^{2}}{2(1+\varepsilon _{n})}}$ .

Die Folge der $\varepsilon _{n}$ ist also bei gegebenem relativen Fehler $\varepsilon _{0}$ der Startnäherung unabhängig von .

Geometrische Veranschaulichung des Heron-Verfahrens

Dem Heron-Verfahren liegt die Idee zu Grunde, dass ein Quadrat mit Flächeninhalt eine Seitenlänge von ${\sqrt {A}}$ hat. Ausgangspunkt des Verfahrens ist ein beliebiges Rechteck mit Flächeninhalt . Schritt für Schritt wird das Seitenverhältnis des Rechtecks so geändert, dass sich seine Form immer mehr der eines Quadrats annähert, während der Flächeninhalt gleich bleibt. Die Seitenlängen des Rechtecks sind die Näherungswerte für ${\sqrt {A}}$ .

Im ersten Schritt wird eine beliebige Seitenlänge $x_{0}$ für das Rechteck gewählt. Damit dieses den gewünschten Flächeninhalt hat, wird die zweite Seitenlänge mit der Formel

$y_{0}={\frac {A}{x_{0}}}$

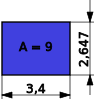
berechnet. Als Beispiel soll die Wurzel aus 9 berechnet werden. Für die eine Seitenlänge wird der Wert 9 gewählt, sodass sich die andere Seitenlänge zu 1 berechnet. Das erste Rechteck hat deshalb die folgende Form.

Part 1 of a geometric example of Herons method.svg

Die Ähnlichkeit dieses Rechteckes mit einem Quadrat ist gering. Das kommt auch dadurch zum Ausdruck, dass die Seitenlängen 1 und 9 sehr schlechte Näherungen für die Wurzel aus 9 sind.

Um eine bessere Annäherung an ein Quadrat zu erhalten, muss die lange Seite gekürzt und die kurze Seite verlängert werden. Als neue Länge der langen Seite wird der Mittelwert

$x_{1}={\frac {x_{0}+y_{0}}{2}}$

der beiden bisherigen Seitenlängen genommen. Die Länge der anderen Seite berechnet sich wie oben zu

$y_{1}={\frac {A}{x_{1}}}$

Im Beispiel ergibt sich als Mittelwert die Seitenlänge 5. Die dazugehörige kurze Seite hat eine Länge von 1,8.

Part 2 of a geometric example of Herons method.svg

Auch hier ist die Ähnlichkeit zu einem Quadrat noch gering. Allerdings ist das neue Rechteck im Vergleich zum vorhergehenden kompakter.

Der beschriebene Ablauf wird in jedem weiteren Schritt des Heron-Verfahrens wiederholt. Der Mittelwert der Seitenlängen eines Rechtecks entspricht der Länge der langen Seite des neuen Rechtecks und die Länge der kurzen Seite lässt sich daraus jeweils wie oben beschrieben berechnen. Im Beispiel entstehen so in den nächsten zwei Schritten die folgenden beiden Rechtecke.

Part 3 of a geometric example of Herons method.svg

Part 4 of a geometric example of Herons method.svg

Das letzte Rechteck ist schon annähernd quadratisch. Die Seitenlänge 3,024 liegt entsprechend nah bei 3, dem exakten Wert von ${\sqrt {9}}$ .

Implementierung in Software

Das Verfahren eignet sich besonders gut zur Implementierung in Software, da nur Grundrechenarten benötigt werden, s. o. Es wird heute angesichts der breiten Verfügbarkeit numerischer Prozessorhardware aber nur noch selten benötigt.

Wenn dazu noch eine Gleitkommadarstellung mit einem Zweier-Exponenten benutzt wird, wird der Ansatz relativ einfach, als Beispiel wird die Wurzel aus 5 betrachtet und der relative Fehler zum Endwert (also abs((x_i - x) / x)) verfolgt:

Zunächst wird von diesem Zweier-Exponenten eine gerade Anzahl abgespaltet, so dass als Exponent entweder eine 0 oder 1 übrig bleibt, die Zahl also auf das Intervall [ ½ , 2 ] normalisiert wird. In diesem Intervall ist die Wurzelfunktion eine nur schwach gekrümmte Kurve, lässt sich also numerisch gut behandeln. Beispiel: IMG class="text" style="width: 54.5ex; height: 3.5ex; vertical-align: -1.17ex;" alt="{\displaystyle {\sqrt {5}}={\sqrt {4\cdot 1{,}25}}=2\cdot {\sqrt {1{,}25}}\approx 2\cdot 1{,}118034=2{,}236068}" src="/svg/e6afef74e027bf3e0f688bfdf4c150e0e9b92c5e.svg">, es wird also vorerst nur noch a=1,25 mit dem Ziel x=1,118034 behandelt.
Als Startwert für die eigentliche Iteration approximiert man diese Kurve durch eine noch einfachere, die sich direkt (ohne Iteration) berechnen lässt. Mit dieser Anfangsberechnung wird der Startwert ermittelt, mit dem die folgende Iteration begonnen wird. Man kann diese Kurve mehr oder weniger aufwendig ansetzen, mit den steigend komplizierteren Ansätzen unten lässt sich ggf. ein Iterationsschritt einsparen:
- eine einfache Konstante (beispielsweise 1),
  Beispiel: x₀ = 1; rel. Fehler=1,1*10⁻¹;
- eine Gerade mit Steigung 1/2 und einer additiven Konstante von 1/2 (als Vereinfachung des nachfolgenden Falls),
  Beispiel: x₀=1/2+1,25/2=1,125; rel. Fehler=6,2*10⁻³;
- eine Gerade mit Steigung 1/2 und einer additiven, optimierten Konstante von $\left(2\cdot {\sqrt[{4}]{2}}-{\sqrt {2}}\right)^{2}/2\approx 0{,}4648415$ ,
  Beispiel: x₀=0,929683/2+1,25/2=1,089841; rel. Fehler=2,5*10⁻²;
- eine Gerade mit optimierter Steigung und einer additiven Konstante (hier nicht näher betrachtet).
Ausgehend von dem so ermittelten Startwert x₀ führt man eine feste Anzahl von Iterationsschritten durch. Die nötige Anzahl, um die gewünschte Genauigkeit zu erreichen, lässt sich dank der obigen Fehlerabschätzung als Worst Case innerhalb des Startintervalls direkt ausrechnen. Bei 32 Bits Mantisse und dem mittleren Startansatz braucht man beispielsweise nur drei Schritte. Diese fest gewählte Anzahl erspart wesentlich aufwendigere Abfragen auf Erreichung der Genauigkeit. Der Ersatz der genannten Konstanten durch die Zahl 1,0 ändert daran nichts. Auch der noch kompliziertere Ansatz brächte zumindest bei dieser Genauigkeit keine Einsparung eines weiteren Iterationsschritts. Bei höheren Genauigkeitsanforderungen kann das anders aussehen.
Beispiel mit drei Schritten nach Ansatz 1 (Konstante 1, mit den anderen Ansätzen konvergiert es noch einen Schritt schneller):
x₁=(x₀+a/x₀)/2=(1+1,25/1)/2=1,125; rel. Fehler=6,2*10⁻³
x₂=(x₁+a/x₁)/2=(1,125+1,25/1,125)/2=1,118056; rel. Fehler=2,0*10⁻⁵
x₃=(x₂+a/x₂)/2=(1,118056+1,25/1,118056)/2=1,118034; rel. Fehler=0
Man sieht die Wirkung der quadratischen Konvergenz, dass sich der Fehler von Schritt zu Schritt jeweils quadriert oder die Anzahl gültiger Stellen bzw. der negative Fehlerexponent grob verdoppelt.
Zum Schluss wird der Exponent restauriert, indem man die Hälfte des im ersten Schritt abgespalteten Werts wieder hinzufügt.
Beispiel: x =2 * x₃ = 2,236068 .

Verallgemeinerung des Verfahrens

Dieses Verfahren lässt sich verallgemeinern, so dass ${\sqrt[{k}]{a}}$ für a>0 berechnet wird. Je größer ist, desto mehr Schritte werden benötigt, um die Wurzel genau zu berechnen.

Dabei wird das Newton-Verfahren zur Bestimmung der positiven Nullstelle ${\sqrt[{k}]{a}}$ der Funktion $f(x)=x^{k}-a$ angewandt. Mit $f'(x)=kx^{k-1}$ folgt aus der Rekursionsformel des Newton-Verfahrens $x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}$ die Iterationsvorschrift:

$x_{n+1}=x_{n}-{\frac {x_{n}^{k}-a}{kx_{n}^{k-1}}}={\frac {(k-1)x_{n}^{k}+a}{kx_{n}^{k-1}}}={\frac {1}{k}}\left((k-1)x_{n}+{\frac {a}{x_{n}^{k-1}}}\right).$

Beispielsweise lautet die rekursive Formel zur Berechnung der Kubikwurzel:

$x_{n+1}=x_{n}-{\frac {x_{n}^{3}-a}{3x_{n}^{2}}}={\frac {2x_{n}^{3}+a}{3x_{n}^{2}}}={\frac {1}{3}}\left(2x_{n}+{\frac {a}{x_{n}^{2}}}\right).$

Hier muss die Folge mit einem geeigneten Startwert $x_{0}$ für den gesuchten Wert von ${\sqrt[{k}]{a}}$ gestartet werden.

Für ganzzahliges positives gelten die gleichen Konvergenzaussagen wie oben für k=2.

Bestimmung des Kehrwerts

Für k=-1 erhält man ein Verfahren, mit dem (ohne Verwendung der Division!) der Kehrwert ${\sqrt[{-1}]{a}}=1/a$ näherungsweise errechnet werden kann:

$x_{n+1}={\frac {(-1-1)x_{n}^{-1}+a}{(-1)x_{n}^{-1-1}}}=2x_{n}-ax_{n}^{2}=(2-ax_{n})\cdot x_{n}.$

Dieses Verfahren konvergiert für alle $x_{0}\in \left(0,2/a\right)$ quadratisch gegen 1/a.

Die Iteration ermöglichte für erste Computer ohne eingebaute Division die Zurückführung dieser Operation auf Multiplikation und Subtraktion. Die Division von zwei Zahlen wurde so ausgeführt, dass der Kehrwert des Nenners bestimmt wurde und mit dem Zähler multipliziert wurde.

Beispiel

Es soll 1/3 näherungsweise berechnet werden mit dem Startwert $x_{0}={\frac {1}{2}}<{\frac {2}{3}}$ :

$x_{1}=\left(2-3\cdot {\frac {1}{2}}\right)\cdot {\frac {1}{2}}={\frac {1}{4}}=0{,}25,$

$x_{2}=\left(2-3\cdot {\frac {1}{4}}\right)\cdot {\frac {1}{4}}={\frac {5}{16}}=0{,}3125,$

$x_{3}=\left(2-3\cdot {\frac {5}{16}}\right)\cdot {\frac {5}{16}}={\frac {85}{256}}=0{,}33203125.$

Für den Startwert $x_{0}={\frac {2}{3}}$ erhält man

$x_{1}=\left(2-3\cdot {\frac {2}{3}}\right)\cdot {\frac {2}{3}}=0,$

$x_{2}=\left(2-3\cdot 0\right)\cdot 0=0,$

somit keine Konvergenz gegen den gesuchten Wert von ${\frac {1}{3}}.$

Historisches

Das Verfahren war in Mesopotamien bereits zur Zeit von Hammurapi I. (ca. 1750 v. Chr.), eines Königs von Babylon, bekannt. Um 100 n. Chr. wurde es von Heron von Alexandria im ersten Buch seines Werkes Metrica beschrieben.

Literatur

Bernd Ziegenbalg: Algorithmen: Von Hammurapi bis Gödel. Harri Deutsch Verlag 2007, ISBN 978-3-8171-1814-4.
Hans R. Schwarz, Norbert Köckler: Numerische Mathematik. 6. Auflage. Teubner, Stuttgart 2006, ISBN 3-519-42960-8.

Anmerkungen

↑ Startwert: Sofern der Ausgangswert bereits als Binärzahl (im Stellenwertsystem) vorliegt, kann einfach gezählt werden, an welcher Stelle seine höchstwertige '1' steht; Startwert wird dann $1\cdot 2^{i/2}$ . Sofern der Ausgangswert in (Binär-)Exponentialdarstellung vorliegt, kann als Startwert einfach der Exponent halbiert werden (um 1 Bit nach rechts schieben). Siehe auch Abschnitt Implementierung in Software

Basierend auf einem Artikel in:

Wikipedia.de