Homotopieverfahren

Homotopie-Verfahren (auch als Homotopiemethode, Fortsetzungs– oder Einbettungsverfahren bezeichnet) sind Berechnungsmethoden in der numerischen Mathematik zur Bestimmung von Lösungen nichtlinearer Gleichungssysteme. Ziel ist es dabei den Konvergenzbereich eines Verfahrens zur Lösung nichtlinearer Gleichungssysteme (wie zum Beispiel des Newtonverfahrens) zu vergrößern.

Vorbetrachtung

Eine Lösung eines nichtlinearen Gleichungssystems F(x)=0 ist ein Punkt $x\in\R^n$ , der in der Regel nichtlinearen Bedingungen $F_{1}(x)=F_{2}(x)=\cdots =F_{n}(x)=0$ genügt, die zu einer vektorwertigen nichtlinearen Funktion (Abbildung) $F:\,\mathbb{R} ^{n}\to \mathbb{R} ^{n}$ zusammengefasst werden. Bei vielen Anwendungen enthält die Funktion Problemparameter, etwa $t\in\R$ , welche verschiedene Werte annehmen können. Ein bekanntes Beispiel ist das reale Pendel, dessen Schwingungsdauer nichtlinear von der reduzierten Pendellänge abhängt. In diesem Fall lautet das Gleichungssystem korrekter F(x,t)=0 , und auch die Lösung hängt vom Parameter ab und bildet daher eine Lösungskurve $x\colon [0,1]\to \mathbb {R} ^{n}$ mit

$F{\bigl (}x(t),t{\bigr )}=0$ für alle $t\in [0,1]$

Als möglicher Bereich des Parameters wurde dabei ohne Beschränkung der Allgemeinheit das Intervall [0,1] gewählt. Die Existenz einer glatten Kurve folgt unter geeigneten Voraussetzungen aus dem Satz über implizite Funktionen. Homotopie-Verfahren sind numerische Verfahren, die solche implizit definierten Kurven verfolgen.

Homotopie für nichtlineare Gleichungssysteme

Eine prinzipielle Schwierigkeit beim Einsatz des Newton-Verfahrens ist die Bestimmung einer Start-Näherung, die nahe genug an der Lösung ${\hat {x}}$ liegen muss, um Konvergenz zu erreichen. Dieses Problem kann man durch Einbettung in eine Homotopie und die Verfolgung der Lösungskurve umgehen. Es sei jetzt $G(x)=0,\ x\in \mathbb{R} ^{n}$ das zu lösende nichtlineare Gleichungssystem mit Lösung ${\hat {x}}$ . Dann kann man etwa durch

$F(x,t)=0,\quad F(x,t):=G(x)-(1-t)G(y),\quad t\in [0,1],$

mit einem festen $y\in \mathbb{R} ^{n}$ ein Hilfsproblem definieren, dessen Lösung man an der Stelle t=0 kennt: $0{\stackrel !=}F(x,0)=G(x)-G(y)$ ergibt offensichtlich x(0)=y . Andererseits ist die mit gesuchte Lösung gerade die an der Stelle t=1 : $0{\stackrel !=}F(x,1)=G(x)$ , also ${\hat x}=x(1)$ . Mit den im folgenden Abschnitt beschriebenen Verfahren kann nun die Kurve x(t) von der bekannten Lösung in t=0 zur gesuchten in t=1 verfolgt werden.

Numerische Kurvenverfolgung

Das schon erwähnte Newton-Verfahren konvergiert sehr schnell (quadratisch), aber nur lokal bei genügend genauer Startnäherung. Dies wird bei der Kurvenverfolgung ausgenutzt, dass der Parameter in kleinen Schritten vergrößert wird, etwa von $0\leq t_{{m-1}}$ auf $t_{m}=t_{{m-1}}+h_{m}\,$ . Dann ist die alte Lösung $x(t_{{m-1}})$ für eine kleine Schrittweite $h_{m}$ eine gute Startnäherung für das Problem $F(x(t_{m}),t_{m})=0$ :

Trivialer Prädiktor

$\,\!x_{0}(t_{m}):=x(t_{{m-1}})$ ,

Korrektoriteration

$\left.{\begin{array}{rl}D_{x}F(x_{k}(t_{m}),t_{m})v_{k}=&-F(x_{k}(t_{m}),t_{m}),\\[0.3em]x_{{k+1}}(t_{m})=&x_{k}(t_{m})+v_{k},\end{array}}\right\}k=0,1,\ldots .$

Dabei ist $\,\!D_{x}F$ eine Kurzschreibweise für die quadratische Jacobi-Matrix der partiellen Ableitungen nach den Variablen $x_{1},\ldots ,x_{n}$ .

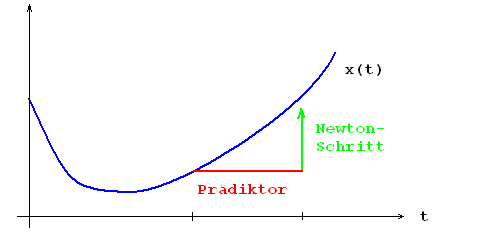
Sie bildet die Matrix des linearen Gleichungssystems, das in jedem Newtonschritt für die Korrekturen s_k zu lösen ist. Eine Skizze dieses Vorgehens zeigt das erste Diagramm. Newtonschritt mit trivialem Prädiktor

Das zweite Diagramm verdeutlicht, dass man eine bessere Startnäherung erhält, wenn man vom Punkt $x(t_{{m-1}})$ aus in Richtung der Kurventangente geht. Die Tangente kann mit Hilfe der Kettenregel bestimmt werden. Denn da die Funktion F(x(t),t) identisch verschwindet, tut dies auch ihre Ableitung,

$0\equiv {\frac {d}{dt}}F(x(t),t)=D_{x}F(x(t),t)x'(t)+D_{t}F(x(t),t).$

Im Punkt $t_{{m-1}}$ kann also die Tangentenrichtung $z_{{m-1}}:=x'(t_{{m-1}})$ aus einem linearen Gleichungssystem bestimmt werden. Dieses Verfahren lautet folgendermaßen:

Tangentialer Prädiktor

$\left.{\begin{array}{rl}D_{x}F{\big (}x(t_{{m-1}}),t_{{m-1}}{\big )}z_{{m-1}}=&-D_{t}F{\big (}x(t_{{m-1}}),t_{{m-1}}{\big )},\\[0.3em]x_{0}(t_{m})=&x(t_{{m-1}})+h_{m}z_{{m-1}},\end{array}}\right\}$

Korrektoriteration

$\left.{\begin{array}{rl}D_{x}F(x_{k}(t_{m}),t_{m})v_{k}=&-F(x_{k}(t_{m}),t_{m}),\\x_{{k+1}}(t_{m})=&x_{k}(t_{m})+v_{k},\end{array}}\right\}k=0,1,\ldots .$

Gegenüber dem einfachen Verfahren wurde nur die erste Gleichung ersetzt.

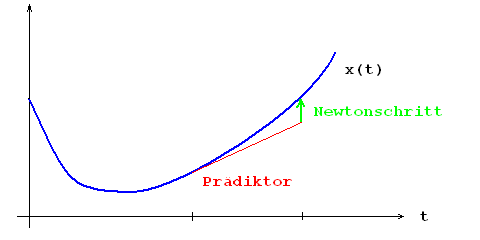
Newtonschritt mit Tangential-Prädiktor

Das Diagramm zeigt, dass der Startfehler, den die (grün gezeichneten) Newtonschritte überbrücken müssen, in der Regel wesentlich kleiner als beim trivialen Prädiktor ist, bei einer glatten Kurve in der Größenordnung $O(h_{m}^{2})$ . Diese Verbesserung erfordert sogar nur einen unwesentlichen Zusatzaufwand, denn die Matrix $D_{x}F{\big (}x(t_{{m-1}}),t_{{m-1}}{\big )}$ entspricht der aus dem Newtonschritt. Man kann daher die letzte LR-Zerlegung aus dem Newton-Verfahren für $x(t_{{m-1}})$ zur Berechnung der Tangente $z_{{m-1}}$ wiederverwenden.

Bei der praktischen Durchführung versucht man, die Konvergenz des Newton-Verfahrens durch Schrittweitensteuerung sicherzustellen. Dazu wählt man die Schrittweite $h_{m}$ so, dass die Kontraktion in den beiden ersten Newton-Schritten genügend klein ist, insbesondere kleiner eins. Wenn sich das gewählte $h_{m}$ nachträglich als zu groß herausstellt und das Newton-Verfahren schlecht oder gar nicht konvergiert, wiederholt man den Schritt $t_{{m-1}}\to t_{m}=t_{{m-1}}+h_{{m-1}}$ mit einem kleineren $h_{m}$ .

Verfolgung allgemeiner Kurven

Die beschriebenen Verfahren arbeiten nur dann problemlos, wenn die Funktion F genügend oft differenzierbar ist und die Jacobi-Matrix $D_{x}F$ überall regulär ist. Gilt letzteres nicht mehr, können Umkehrpunkte und Verzweigungspunkte der Kurve auftreten.

Nach Umkehrpunkten verläuft die Kurve „rückwärts“, in Verzweigungspunkten spaltet sie sich auf. In beiden Fällen ist daher eine (eindeutige) Parametrisierung nach der Variable t nicht mehr möglich. Daher betrachtet man t einfach als (n+1) -te Komponente der Unbekannten bei $y=(x_{1},\ldots ,x_{n},t)^{T}$ und parametrisiert die Kurve nach ihrer Bogenlänge s. Dann sucht man alle Lösungen

$y(s):\quad F(y(s))=0$ , wobei $F:\,\mathbb{R} ^{{n+1}}\to \mathbb{R} ^{n}$

ist. Dieses Gleichungssystem ist unterbestimmt und hat unendlich viele Lösungen, die unter geeigneten Voraussetzungen eine glatte Lösungskurve y(s) bilden.

Wie zuvor folgt aus der Kettenregel $F'(y(s))y'(s)\equiv 0$ , dass die Tangentenrichtung y'(s) das homogene Gleichungssystem mit der vollen Jacobimatrix $F'=\partial F/\partial y\in \mathbb{R} ^{{n\times (n+1)}}$ erfüllt, also im Kern dieser Matrix liegt. Damit kann also wieder ein Prädiktor berechnet werden. Auch das Newton-Verfahren ist durchführbar, indem man eine Richtung wählt, die orthogonal zur Kurventangente, also zum Kern von F'(y) liegt. Diese Richtung wird automatisch durch die Moore-Penrose-Pseudoinverse von berechnet. Bei diesem Verfahren wird eine Approximation an die Bogenlänge s schrittweise vergrößert:

Allgemeiner Prädiktor-Korrektor-Schritt

${\begin{array}{rl}F'{\big (}y(s_{{m-1}}){\big )}z_{{m-1}}&=0,\ \|z_{{m-1}}\|_{2}=1,\\s_{m}&:=s_{{m-1}}+h_{m},\\y_{0}(s_{m})&:=y(s_{{m-1}})+h_{m}z_{{m-1}};\\y_{{k+1}}(s_{m})&:=y_{k}(s_{m})-{\Big (}F'(y_{k}(s_{m})){\Big )}^{+}\,F(y_{k}(s_{m})),\ k=0,1,\ldots .\end{array}}$

Die Bezeichnung $(\ldots )^{+}$ bezeichnet dabei die erwähnte Pseudoinverse.

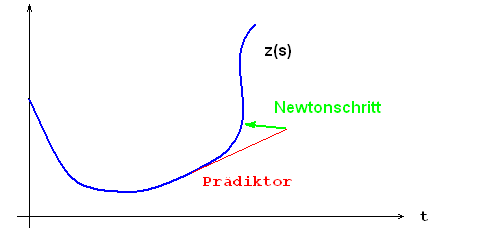
Tangential-Prädiktor und Newtonschritt bei Kurve mit Umkehrpunkten

Das dritte Diagramm skizziert dieses Vorgehen, der (grün gezeichnete) Newtonschritt verläuft ungefähr orthogonal zur Kurve und hat daher auch im Umkehrpunkt (vertikaler Verlauf der Kurve) keine Schwierigkeiten.

Bemerkungen:

Durch die erste Bedingung ist noch nicht die Richtung der Tangente $\pm z_{{m-1}}$ festgelegt. Man wählt das Vorzeichen natürlich so, dass das Innenprodukt $z_{{m-1}}^{T}z_{{m-2}}>0$ ist, um in einer Richtung vorzugehen.
Die beiden Teilschritte können mit der QR-Zerlegung der transponierten Matrix $\,(F'(y))^{T}=QR$ effizient ausgeführt werden. Die Tangentenrichtung erhält man mit einem beliebigen Vektor $u\not =0$ durch Normierung von $\,(E-QQ^{T})u$ , wenn der letzte Ausdruck ungleich null ist.
Die Newton-Korrektur $\,v_{k}=y_{{k+1}}(s_{m})-y_{k}(s_{m})$ berechnet man über $v_{k}=-Q{\tilde v}_{k}$ , wobei der Vektor ${\tilde v}_{k}\in \mathbb{R} ^{n}$ das quadratische Dreiecksystem $R^{T}{\tilde v}_{k}=F(y_{k}(s_{m}))$ löst.

Basierend auf einem Artikel in:

Wikipedia.de