Kugelschale

Kugelschale, rechts: aufgeschnitten

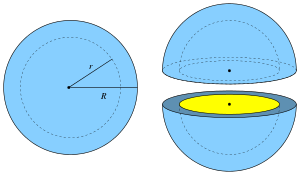
Eine Kugelschale (auch Hohlkugel genannt) ist die Differenzmenge zweier konzentrischer Kugeln mit unterschiedlichem Radius.

Die ebenen Schnitte einer Kugelschale sind Kreisscheiben oder Kreisringe.

Volumen und Oberfläche

Sind die Radien der beiden Kugeln, so ist das Volumen der Kugelschale

und die Oberfläche

.

Schalenmodelle von Himmelskörpern

In den Naturwissenschaften dienen Kugelschalen oft zur Modellierung von inhomogenen Körpern, wenn sie annähernde Kugelgestalt besitzen.

Bei Himmelskörpern - die ab etwa 500 km Größe kugelähnlich sind - werden diese Kugelschalen so angesetzt, dass sie eine konstante Dichte besitzen (mittlere Gesteins- bzw. Gasdichte). Damit ein solcher Himmelskörper im hydrostatischen Gleichgewicht ist, müssen seine (kugelähnlichen) Schichtflächen gleichzeitig Niveauflächen sein.

Einige Beispiele dafür sind:

• Erdinneres: Erdkruste, oberer/unterer Erdmantel, Erdkern
• Erdatmosphäre: Peplo- und Troposphäre, Strato- und Mesosphäre, Ionosphäre
• Terrestrische Planeten: dicke Lithosphäre, sonst erdähnlicher Aufbau
• Gasplaneten: dichte Atmosphäre, flüssige Gashülle, metallischer Wasserstoff, Eisenkern
• Sonne und Fixsterne: Sonnenkorona, Chromosphäre, Photosphäre, Konvektionsschicht, Zone der Kernfusion.

In den Berechnungsmodellen müssen die Kugelschalen noch weitere Bedingungen erfüllen, die vor allem den Druck und den Wärmetransport betreffen. So muss bei einem Stern in stabilem Zustand die Gravitation überall dem Strahlungs- und Gasdruck das Gleichgewicht halten, und die nach außen dringende Energie muss in den äußeren Kugelschalen immer dieselbe sein. Andernfalls gäbe es einen Wärmestau und der Stern würde instabil werden (siehe Supernova).

Schwerelosigkeit im Innern einer Kugelschale

Der Innenraum einer Kugelschale ist schwerelos. Plausibel wird dies durch Zerlegung in symmetrische Schalenteile, deren Gravitationskräfte sich aufheben

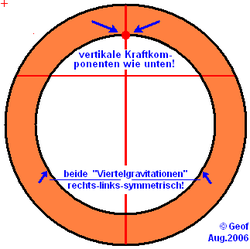
Eine besondere Bedeutung haben Kugelschalen bei der Berechnung des Schwerefeldes. Im Innenraum einer hohlen Kugelschale ist das Schwerepotential konstant, weil sich deren Gravitationskräfte gegenseitig aufheben (siehe Bild). Wenn man daher von einem kugelsymmetrischen Körper Schicht um Schicht „abhebt“ (rechnerisch beseitigt), so ändert sich die Gravitation im verbleibenden Restkörper nicht. Der Geophysiker Karl Ledersteger nennt dies Prinzip der Entblätterung.

Damit lässt sich von jedem größeren Himmelskörper das Schwerefeld relativ genau berechnen. Eine Komplikation ist jedoch die infolge der Rotation und Fliehkraft entstehende Abplattung. Sie ist im Innern kleiner als nahe der Oberfläche, sodass die Parallelität der Schichtung bzw. der Dichteschalen nicht mehr gegeben ist. Die entsprechenden Berechnungen kann man heute aber mittels Computern lösen, indem die Körper in viele kleine Elementarkörper zerlegt werden.

Anwendungen in der Elektrotechnik

Auch bei der Berechnung von Ladungen und Strömen sind die besonderen Eigenschaften von Kugelschalen bedeutsam. So kann man nachweisen, dass sich elektrische Ladungen auf einer leitenden Kugeloberfläche gleichmäßig verteilen. Dies war im 18. Jahrhundert die Voraussetzung, das Coulombsche Gesetz ableiten zu können.

Auch der Effekt des Faradayschen Käfigs lässt sich durch ein Kugelschalen-Modell beweisen, und die Ladungs- und Stromstärke in einem elektrischen Leiter auf analoge Weise.

Weitere Beispiele

Weitere Beispiele von Kugelschalen bzw. Hohlkugeln sind

• Geode (Geowissenschaften), ein rundlicher, durch eine einheitliche Gesteinsaußenschicht begrenzter Hohlraum, mit und ohne mineralische bzw. fossile Füllung
• Druse (Mineralogie), ein teilweise mit Kristallen gefüllter, rundlicher Hohlraum
• Blastula, eine von einer einzigen Zellschicht gebildete Hohlkugel
• Fullerene, Hohlkugeln, die aus einem Netz von Kohlenstoffatomen bestehen
• Baoding-Kugeln, Hohlkugeln mit eingebauten Klangelementen
• Ball, Seifenblase
• eine Kanonenkugel mit Sprengladung

Basierend auf einem Artikel in: Wikipedia.de