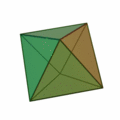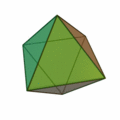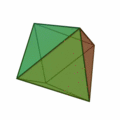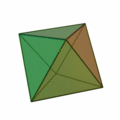
Oktaeder
| Regelmäßiges Oktaeder | |
|---|---|
 | |
| Art der Seitenflächen | gleichseitige Dreiecke |
| Anzahl der Flächen | 8 |
| Anzahl der Ecken | 6 |
| Anzahl der Kanten | 12 |
| Schläfli-Symbol | {3,4} |
| dual zu | Hexaeder (Würfel) |
| Netz | 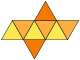 |
| Anzahl verschiedener Netze | 11 |
| Anzahl Kanten in einer Ecke | 4 |
| Anzahl Ecken einer Fläche | 3 |
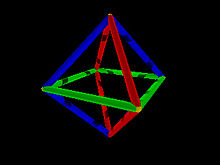
Das (auch, österr.: der) Oktaeder [ɔktaˈeːdɐ] (von griech. oktáedron ‚Achtflächner‘) ist einer der fünf platonischen Körper, genauer ein regelmäßiges Polyeder (Vielflächner) mit
- acht (kongruenten) gleichseitigen Dreiecken als Flächen
- zwölf (gleich langen) Kanten und
- sechs Ecken, in denen jeweils vier Flächen zusammentreffen
Das Oktaeder ist sowohl eine gleichseitige vierseitige Doppelpyramide (mit quadratischer Grundfläche) als auch ein gleichseitiges Antiprisma (mit einem gleichseitigen Dreieck als Grundfläche).
Symmetrie
Wegen seiner hohen Symmetrie – alle Ecken, Kanten und Flächen sind untereinander gleichartig – ist das Oktaeder ein reguläres Polyeder. Es hat:
- drei vierzählige Drehachsen (durch gegenüberliegende Ecken)
- vier dreizählige Drehachsen (durch die Mittelpunkte gegenüberliegender Flächen)
- sechs zweizählige Drehachsen (durch die Mittelpunkte gegenüberliegender Kanten)
- neun Symmetrieebenen (drei Ebenen durch je vier Ecken, sechs Ebenen durch jeweils zwei Ecken und zwei Kantenmittelpunkte)
und ist
- punktsymmetrisch (zentralsymmetrisch)
Insgesamt hat die Symmetriegruppe des Oktaeders – die Oktaeder- oder Würfelgruppe – 48 Elemente.
Beziehungen zu anderen Polyedern
Das Oktaeder ist das zum Hexaeder (Würfel) duale Polyeder (und umgekehrt).
Setzt man auf die Seiten des Oktaeders Tetraeder auf, entsteht das Sterntetraeder.
Mithilfe von Oktaeder und Würfel können zahlreiche Körper konstruiert werden, die ebenfalls die Würfelgruppe als Symmetriegruppe haben. So erhält man zum Beispiel
- das abgestumpfte Oktaeder mit 8 Sechsecken und 6 Quadraten
- das Kuboktaeder mit 8 Dreiecken und 6 Quadraten, also mit 14 Flächen, und 12 Ecken
- den abgestumpften Würfel mit 8 Dreiecken und 6 Achtecken
als Durchschnitte eines Oktaeders mit einem Würfel (siehe archimedische Körper) und
- das Rhombendodekaeder (mit 8 + 6 = 14 Ecken und 12 Rhomben als Flächen)
als konvexe Hülle einer Vereinigung eines Oktaeders mit einem Würfel.
Formeln
| Größen eines Oktaeders mit Kantenlänge a | |
|---|---|
| Volumen | |
| Oberflächeninhalt | |
| Umkugelradius | |
| Kantenkugelradius | |
| Inkugelradius | |
| Verhältnis von Volumen zu Umkugelvolumen |
|
| Flächenwinkel ≈ 109° 28′ 16″ |
|
| 3D-Kanten-Winkel = 90° |
|
| Ecken-Raumwinkel ≈ 0,4327 π |
|
Verallgemeinerung
Die Analoga des Oktaeders in beliebiger Dimension
n werden als (n-dimensionale) Kreuzpolytope
bezeichnet und sind ebenfalls reguläre Polytope. Das n-dimensionale
Kreuzpolytop hat
Ecken und wird von
(n−1)-dimensionalen Simplexen
(als Facetten) begrenzt. Das vierdimensionale
Kreuzpolytop hat 8 Ecken, 24 gleich lange Kanten, 32 gleichseitige Dreiecke als
Seitenflächen und 16 Tetraeder
als Facetten. (Das eindimensionale Kreuzpolytop ist eine Strecke, das
zweidimensionale Kreuzpolytop ist das Quadrat.)
Ein Modell für das n-dimensionale Kreuzpolytop ist die Einheitskugel bezüglich der Summennorm
für
im Vektorraum .
Und zwar ist das (abgeschlossene) Kreuzpolytop daher
- die Menge
-
.
- die konvexe
Hülle der
Eckpunkte
, wobei
die Einheitsvektoren sind.
- der Durchschnitt
der
Halbräume, die durch die Hyperebenen der Form
-
- bestimmt werden und den Ursprung enthalten.
Das Volumen des n-dimensionalen Kreuzpolytops beträgt ,
wobei
der Radius der Kugel um den Ursprung bezüglich der Summennorm ist. Die Beziehung
lässt sich mittels Rekursion und dem Satz
von Fubini beweisen.
Anwendungen

In der Chemie können sich bei der Vorhersage von Molekülgeometrien nach dem VSEPR-Modell oktaedrische Moleküle ergeben. Auch in Kristallstrukturen, wie der kubisch flächenzentrierten Natriumchlorid-Struktur (Koordinationszahl 6), taucht das Oktaeder in der Elementarzelle auf; genauso in der Komplexchemie, falls sich 6 Liganden um ein Zentralatom lagern.
Einige in der Natur vorkommende Minerale, z.B. das Alaun, kristallisieren in oktaedrischer Form aus.
In Rollenspielen werden oktaedrische Spielewürfel verwendet und dort als „W8“, also als Würfel mit 8 Flächen, bezeichnet.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.08. 2023