Raumwinkel
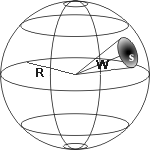
Der Raumwinkel ist das dreidimensionale Gegenstück zum zweidimensionalen für die Ebene definierten Winkel. Er beschreibt den Anteil am gesamten dreidimensionalen Raum, der z.B. im Inneren eines gegebenen Kegel- oder Pyramidenmantels liegt.
Definition
Der Raumwinkel
ist definiert als der Flächeninhalt
einer Teilfläche
einer Kugeloberfläche,
dividiert durch das Quadrat des Radius
der Kugel:
.
Bei Betrachtung der Einheitskugel
(
also betragsgleich dem zugehörigen Raumwinkel. So ist der volle Raumwinkel
gleich der Oberfläche der Einheitskugel, nämlich
.
Die Teilfläche kann von beliebiger Umrissform sein. Vektoriell geschrieben als Flächenintegral ist
.
Dabei ist
der Einheitsvektor
vom Koordinatenursprung,
das differentielle Flächenelement und
dessen Abstand vom
Koordinatenursprung.
Anders als das Bild vielleicht vermuten lässt, spielt die Umrissform des Flächenstücks keine Rolle. Jede Umrissform auf der Kugeloberfläche mit dem gleichen Flächeninhalt definiert einen Raumwinkel der gleichen Größe. Legt man durch jeden Punkt der Umrissform einen Strahl mit dem Mittelpunkt der Kugel als Startpunkt, dann erhält man eine geometrische Figur, die den Raumwinkel veranschaulicht. Dies ist vergleichbar mit der Darstellung für einen Winkel in der Ebene: Zwei Halbgeraden mit einem gemeinsamen Startpunkt.
Maßeinheiten
Obwohl der Raumwinkel eine Größe
der Dimension Zahl ist, wird er zur Verdeutlichung meist in der Einheit Steradiant (sr) angegeben;
dies entspricht dem Bogenmaß
mit der Einheit Radiant
(rad) beim ebenen Winkel. Ein Raumwinkel von 1 sr umschließt auf einer Kugel mit dem Radius 1 m
eine Fläche
von 1 m2. Da eine ganze Kugeloberfläche
den Flächeninhalt
hat, ist der zugehörige volle Raumwinkel
.
Gelegentlich werden Raumwinkel auch in Quadratgrad,
(°)², angegeben. 1 (°)² ist gleich .
Die Verwendung einer Hilfsmaßeinheit für eine Größe der Dimension Zahl hat, wie auf vielen Gebieten, insbesondere auch beim Raumwinkel, den Vorteil, dass schon an der verwendeten Einheit erkennbar ist, welche physikalische Größe gemeint ist. Die Lichtstärke (cd = lm/sr) zeigt im Gegensatz zum Lichtstrom (lm) ihre Abhängigkeit vom Raumwinkel durch das Auftreten des Steradiant in der Einheit. Die Lichtstärke bezeichnet somit einen vom Raumwinkel abhängigen Lichtstrom.
Darstellung mit Vektoren
Drei von einem Punkt
P ausgehende Vektoren ,
und
bestimmen ein allgemeines Dreieck.
Für den aufgespannten Raumwinkel
mit dem Scheitel P gilt:
.
Dabei ist
das Spatprodukt der Vektoren
,
und
,
ist das Skalarprodukt
und
ist die Länge
des Vektors.
Diese Darstellung wurde im Jahr 1983 von Oosterom und Strackee angegeben und bewiesen.
Darstellung mit Kugelkoordinaten

Der Raumwinkel eines Kugeldreiecks
beträgt in Abhängigkeit von seinen Innenwinkeln
Steradiant (siehe Kugeldreieck
- Eigenschaften).
In einem Kugelkoordinatensystem
kann der Raumwinkel besonders übersichtlich definiert werden, da es keine
radiale Variable gibt. Zwei Meridianwinkel ,
und zwei Breitenwinkel
,
bestimmen ein Flächenelement auf einer Kugeloberfläche.
Der zugehörige Raumwinkel beträgt:
Raumwinkel eines Kegels
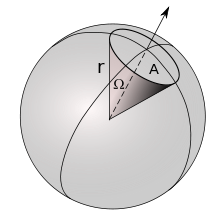
Wählt man als Umrissform auf der Kugeloberfläche
einen Kreis, so
erhält man den kanonischen Raumwinkel. Der Raumwinkel bildet dann den Mantel
eines geraden
Kreiskegels, in dessen Spitze der Mittelpunkt
der Kugel liegt.
Ist
der Öffnungswinkel in der Spitze des Kegels,
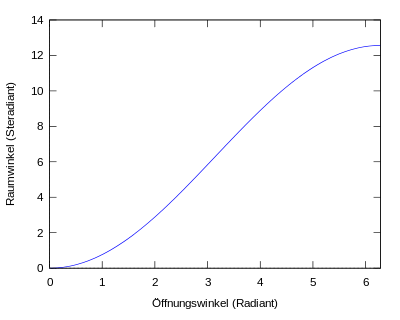
dann ergibt sich der Raumwinkel
aus dem Doppelintegral
| Öffnungswinkel |
0 | 1 | 2 | 5 | 10 | 15 | 30 | 45 | 57,2958 |
|---|---|---|---|---|---|---|---|---|---|
| Öffnungswinkel |
0,0000 | 0,0175 | 0,0349 | 0,0873 | 0,1745 | 0,2618 | 0,5236 | 0,7854 | 1,0000 |
| Raumwinkel |
0,00 | 0,79 | 3,14 | 19,63 | 78,49 | 176,46 | 702,83 | 1570,10 | 2525,04 |
| Raumwinkel |
0,0000 | 0,0002 | 0,0010 | 0,0060 | 0,0239 | 0,0538 | 0,2141 | 0,4783 | 0,7692 |
| Öffnungswinkel |
60 | 65,5411 | 75 | 90 | 120 | 150 | 180 | 270 | 360 |
| Öffnungswinkel |
1,0472 | 1,1439 | 1,3090 | 1,5708 | 2,0944 | 2,6180 | 3,1416 | 4,7124 | 6,2832 |
| Raumwinkel |
2763,42 | 3282,81 | 4262,39 | 6041,36 | 10313,24 | 15287,95 | 20626,48 | 35211,60 | 41252,96 |
| Raumwinkel |
0,8418 | 1,0000 | 1,2984 | 1,8403 | 3,1416 | 4,6570 | 6,2832 | 10,7261 | 12,5664 |
Raumwinkel einer Pyramide
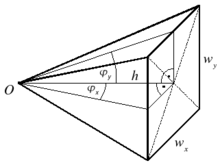
Der Spezialfall des Raumwinkels mit einem rechteckigen und ebenen Umriss entspricht der geometrischen Form einer Pyramide, wobei der Ursprung genau senkrecht über dem Mittelpunkt des ebenen Rechtecks stehe, (siehe Abbildung). Dieser Raumwinkel tritt z.B. bei der Berechnung der Étendue von optischen Systemen mit rechteckigen Aperturen auf.
Er lässt sich sehr leicht mit der Oosterom-und-Strackee-Formel berechnen. Mit
den Pyramidengrundseiten
und
sowie der Höhe h ergibt sich:
Verwendet man für die Berechnung die beiden Öffnungswinkel
und
,
wobei
und
ist, so folgt nach einigen trigonometrischen
Umformungen:
Beispiele
Eine Rechteckblende vor einer Punktlichtquelle grenze den Lichtstrahl auf die
Winkel 45°
()
und 20° (
)
ein. Der Raumwinkel beträgt 0,27 sr.
Handelt es sich um eine quadratische Blende und beide Winkel sind 20° groß, dann umfasst der Raumwinkel 0,12 sr. Der kanonische Raumwinkel einer 20°-Kreisblende liegt bei 0,10 sr.
Raumwinkel eines Polyeders
Der Raumwinkel in der Ecke eines Polyeders kann mit dem Satz von L'Huilier berechnet werden.
Für den Raumwinkel, der in der Ecke
mit den Innenwinkeln ,
,
liegt, gilt
wobei ,
,
und
ist.
Beispiele
Die folgenden Raumwinkel ergeben sich mithilfe der Halbwinkelformeln,
der Additionstheoreme
für den Tangens
und der Gleichungen ,
und
.
Regelmäßiges Tetraeder
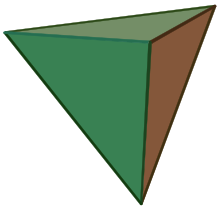
Ein regelmäßiges
Tetraeder hat 4 Ecken mit jeweils 3 gleichen Innenwinkeln von 60°, denn
alle 4 Seitenflächen
sind gleichseitige
Dreiecke. Es gilt also
und
Quadratische Pyramide
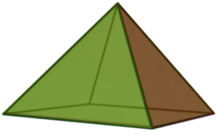
Eine gerade quadratische
Pyramide, die ein Quadrat
und vier gleichseitige
Dreiecke als Seitenflächen
hat, besitzt an der quadratischen
Grundfläche
4 Ecken mit den Innenwinkeln ,
,
.
Für den Raumwinkel in diesen 4 Ecken gilt
Oktaeder
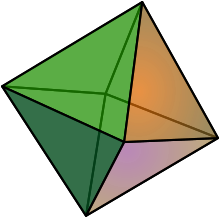
Ein Oktaeder besteht aus 2 kongruenten geraden quadratischen Pyramiden, die jeweils ein Quadrat und 4 gleichseitige Dreiecke als Seitenflächen haben. Der Raumwinkel in den 6 Ecken des Oktaeders - und in der Spitze der quadratischen Pyramide - ist daher doppelt so groß wie der Raumwinkel in den anderen 4 Ecken der quadratischen Pyramide und beträgt
Prisma
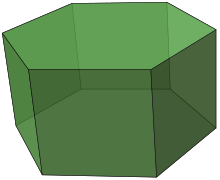
Eine gerades Prisma
hat Ecken mit
einem beliebigen Innenwinkel
und zwei rechten
Winkeln von 90°, denn die Mantelfläche
eines geraden Prismas besteht aus Rechtecken.
Für den Raumwinkel in den Ecken gilt
Dieser Raumwinkel hat offensichtlich denselben Anteil am vollen Raumwinkel
wie der Innenwinkel
am zweidimensionalen
Vollwinkel
.
Oktaederstumpf

Ein Oktaederstumpf
hat 24 Ecken, wo
jeweils ein Quadrat und zwei regelmäßige
Sechsecke
zusammentreffen. Jede Ecke hat also die Innenwinkel
,
,
und den Raumwinkel
Die Raumwinkel in den Ecken
des Oktaederstumpfs
sind also gleich
des vollen Raumwinkels. Dieses Ergebnis wird dadurch bestätigt, dass sich der dreidimensionale
euklidische
Raum lückenlos mit kongruenten
Oktaederstümpfen ausfüllen lässt, wobei in jeder Ecke 4 Oktaederstümpfe
zusammentreffen (siehe Raumfüllung).


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.08. 2023