Eisenstein-Zahl

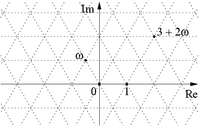
Eisenstein-Zahlen als Punkte eines Dreiecksgitters in der komplexen Zahlenebene

Die Eisenstein-Zahlen sind eine Verallgemeinerung der ganzen Zahlen auf die komplexen Zahlen. Sie sind nach dem deutschen Mathematiker Gotthold Eisenstein, einem Schüler von Gauß, benannt. Die gaußschen Zahlen sind eine andere Verallgemeinerung der ganzen Zahlen auf die komplexen Zahlen. Die Eisenstein-Zahlen sind der Ganzheitsring, also die Maximalordnung des quadratischen Zahlkörpers ${\mathbb {Q}}\left({\sqrt {-3}}\right)$ , der mit dem 3. Kreisteilungskörper ${\mathbb Q}(\mu _{3})$ übereinstimmt. Sie treten beispielsweise bei der Formulierung des kubischen Reziprozitätsgesetzes auf (→ siehe Kubisches Reziprozitätsgesetz in diesem Artikel).

Definition

Eine komplexe Zahl ist eine Eisenstein-Zahl, wenn sie sich in der Form

$E=a+b\,\omega$ mit $\omega =e^{{2\pi {\mathrm i}/3}}=-{\frac 12}+{\frac {{\mathrm i}}2}{\sqrt 3}$

und ganzen Zahlen und darstellen lässt. $\omega$ ist eine (primitive) dritte Einheitswurzel und erfüllt somit die Gleichung

$\omega ^{2}+\omega +1=0.$

Im Folgenden bezeichnet $\omega$ immer genau die oben genannte primitive Einheitswurzel, nicht die zu $\omega$ konjugiert komplexe zweite Nullstelle dieser quadratischen Gleichung.

Mit anderen Worten: Die Eisensteinzahlen bilden den Ring $\mathbb{Z } [\omega ]$ , der aus dem Ring der ganzen Zahlen durch Adjunktion der primitiven 3. Einheitswurzel $\omega$ entsteht. Der Ganzheitsring des Kreisteilungskörpers, der aus $\mathbb {Q}$ durch Adjunktion einer primitiven 6. Einheitswurzel, zum Beispiel durch Adjunktion des Hauptwertes $-\omega ^{2}=_{H}{\sqrt[ {3}]{-1}}=e^{{\pi {\mathrm i}/3}}$ entsteht, $\mathbb{Z } [-\omega ^{2}]$ , stimmt ebenfalls mit den Eisenstein-Zahlen überein.

Geometrische Bedeutung

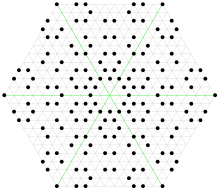
„Kleine“ Primelemente unter den Eisenstein-Zahlen in der komplexen Zahlenebene. Die Rotationssymmetrie um 60° folgt aus der Existenz von sechs Einheiten in $\mathbb{Z } [\omega ]$ .

Die Eisenstein-Zahlen bilden ein Dreiecksgitter in der gaußschen Zahlenebene. Sie entsprechen den Mittelpunkten einer dichtesten Kugelpackung in zwei Dimensionen.

Zahlentheorie

Auf den Eisenstein-Zahlen lässt sich Zahlentheorie betreiben: Die Einheiten sind genau die sechs komplexen Nullstellen der Gleichung $X^{6}=1$ , die zyklische Einheitengruppe wird also von jeder der beiden primitiven 6. Einheitswurzeln $e^{{+2\pi i/6}}=-\omega ^{2}$ bzw. $e^{{-2\pi i/6}}=-\omega$ erzeugt. Zu jeder von $0$ verschiedenen Eisensteinzahl $\alpha$ existieren genau sechs assoziierte Elemente, die in der multiplikativen Gruppe des Körpers ${\mathbb {Q}}\left({\sqrt {-3}}\right)$ eine Nebenklasse $\alpha U$ bilden.

Man kann Primelemente analog zu den Primzahlen in $\mathbb {Z}$ definieren und zeigen, dass die Primfaktorzerlegung einer Eisenstein-Zahl – bis auf Assoziiertheit und Reihenfolge der Primfaktoren – eindeutig ist. Die Eisensteinzahlen bilden also einen faktoriellen Integritätsbereich. Alle ganzen Zahlen der Form $m^{2}+3n^{2}$ sind in den Eisenstein-Zahlen zerlegbar. Dort sind daher die Zahlen 3, 7, 13, 19, … keine Primelemente.

Genauer treten die folgenden drei Fälle auf:

3 ist ein Sonderfall: $3=-\omega ^{2}(1-\omega )^{2}$ . Dies ist die einzige Primzahl in $\mathbb {Z}$ , die durch das Quadrat eines Primelementes in $\mathbb{Z } [\omega ]$ teilbar ist. Man sagt in der algebraischen Zahlentheorie, diese Primzahl sei verzweigt.

Positive Primzahlen $p\in \mathbb{Z }$ , die die Kongruenz $p\equiv 2{\pmod 3}$ erfüllen, bleiben auch in $\mathbb{Z } [\omega ]$ prim. So eine Primzahl nennt man träge.

Positive Primzahlen $p\in \mathbb{Z }$ , die die Kongruenz $p\equiv 1{\pmod 3}$ erfüllen, werden in $\mathbb{Z } [\omega ]$ zu Produkten von zwei zueinander komplex konjugierten Primelementen Man sagt, solche Primzahlen seien zerlegt.

Die trägen Primzahlen sind also $2,5,11,17,23,\ldots$ und eine Primfaktorisierung der ersten zerlegten Primzahlen lautet:

$7=(3+\omega )\cdot (2-\omega ),\quad 13=(4+\omega )\cdot (3-\omega ),\quad 19=(3-2\omega )\cdot (5+2\omega ),\ldots$

Die sechs mit einem Primelement assoziierten Elemente sind prim, ebenso das zu einem Primelement $\alpha$ komplex konjugierte Element $\overline {\alpha }$ .

Da die Norm $N(\alpha )=\alpha \cdot \overline {\alpha }$ eines Elementes von $\mathbb{Z } [\omega ]$ stets in $\mathbb {Z}$ liegt, bilden $1-\omega$ , die trägen ganzen Primzahlen und die Primelemente, die als Faktoren bei der Zerlegung der zerlegten ganzen Primzahlen auftreten, zusammen mit ihren Assoziierten die Menge aller Primelemente in $\mathbb{Z } [\omega ]$ .

Der Ring der Eisenstein-Zahlen ist euklidisch.

Kubischer Rest-Charakter

Im Ring der Eisensteinschen Zahlen gilt ein Satz, der analog zum kleinen fermatschen Satz der elementaren Zahlentheorie ist:

Sind $\alpha ,\rho \in \mathbb{Z } [\omega ]$ und $\rho$ ein Primelement, das $\alpha$ nicht teilt, dann gilt:

$\alpha ^{{N(\rho )-1}}\equiv 1{\pmod {\rho }}$

Wenn nun für die Norm von $\rho$ gilt, dass $N(\rho )\neq 3$ und also IMG class="text" style="width: 20.18ex; height: 2.84ex; vertical-align: -0.83ex;" alt="N(\rho )\equiv 1{\pmod 3}" src="/svg/200bef9739d79ea29260e473bd271c9688f3a55f.svg"> ist, dann ist $\alpha ^{{{\frac {N(\rho )-1}{3}}}}$ eine Potenz mit ganzzahligem Exponenten und es gilt:

$\alpha ^{{{\frac {N(\rho )-1}{3}}}}\equiv \omega ^{k}{\pmod {\rho }}$ für eine eindeutig bestimmte 3. Einheitswurzel $\omega ^{k}$

Man nennt diese Einheitswurzel den kubischen Rest-Charakter von $\alpha$ modulo $\rho$ und schreibt dafür:

$\left({\frac {\alpha }{\rho }}\right)_{3}=\omega ^{k}\equiv \alpha ^{{{\frac {N(\rho )-1}{3}}}}{\pmod {\rho }}$

Die Bezeichnung als Charakter ergibt sich daraus, dass die Abbildung bei festem Primelement $\rho$ einen unitären Charakter auf der multiplikativen Gruppe des Körpers $\mathbb{Z } [\omega ]/(\rho )$ bestimmt.

Die Kongruenz $x^{3}\equiv \alpha {\pmod \rho },\;(\alpha \not \equiv 0{\pmod \rho })$ ist in $Z[\omega ]$ genau dann lösbar, wenn $\left({\frac {\alpha }{\rho }}\right)_{3}=1$ gilt. Ist die Kongruenz lösbar und $\alpha \not \equiv 0{\pmod \rho }$ , dann nennt man $\alpha$ einen kubischen Rest modulo $\rho$ ; ist die Kongruenz unlösbar, einen kubischen Nichtrest modulo $\rho$ . Ebenso werden die Begriffe kubischer Rest und Nichtrest allgemeiner erklärt, wenn $\rho$ zwar teilerfremd zu $\alpha$ , aber kein Primelement ist.

Der kubische Rest-Charakter hat für Primelemente $\rho$ , die nicht zu $1-\omega$ assoziiert sind, formale Eigenschaften, die den Eigenschaften des Legendre-Symbols ähneln:

$\left({\frac {\alpha \beta }{\rho }}\right)_{3}=\left({\frac {\alpha }{\rho }}\right)_{3}\left({\frac {\beta }{\rho }}\right)_{3}$
$\overline {\left({\frac {\alpha }{\rho }}\right)_{3}}=\left({\frac {\overline {\alpha }}{\overline {\rho }}}\right)_{3}$ , wobei der Überstrich für die komplexe Konjugation steht.
Sind $\rho$ und $\theta$ assoziierte Primelemente, dann gilt $\left({\frac {\alpha }{\rho }}\right)_{3}=\left({\frac {\alpha }{\theta }}\right)_{3}$ .
Ist $\alpha \equiv \beta {\pmod \rho }$ , dann gilt $\left({\frac {\alpha }{\rho }}\right)_{3}=\left({\frac {\beta }{\rho }}\right)_{3}$ .

Der kubische Rest-Charakter kann im „Nenner“ multiplikativ auf zusammengesetzte Zahlen fortgesetzt werden, die teilerfremd zu 3 sind. Dabei wird dann ergänzend definiert, dass das so definierte kubische Restsymbol $\left({\frac {\alpha }{\lambda }}\right)_{3}$ den Wert 0 hat, falls die Zahlen $\alpha ,\lambda$ im Ring der Eisenstein-Zahlen nicht zueinander teilerfremd sind, aber $\lambda$ teilerfremd zu 3 ist. Diese Verallgemeinerung ist analog zu der Verallgemeinerung des Legendre-Symbols zum Jacobi-Symbol bis auf die Tatsache, dass für den Fall, dass $\lambda \equiv 0{\pmod {1-\omega }}$ gilt oder gleichwertig, dass die Norm von $\lambda$ in $\mathbb {Z}$ von 3 geteilt wird, kein Wert für das Symbol definiert wird. Manchmal wird im zuletzt genannten Fall das Symbol 0 gesetzt. Diese Variante ändert an den folgenden Aussagen nichts.

Ähnlich wie beim Jacobi-Symbol gelten für einen „Nenner“ $\lambda$ des kubischen Restsymbols, der kein Primelement ist, folgende Aussagen:

Durch die multiplikative Fortsetzung gilt nach Definition:

$\left({\frac {\alpha }{\lambda }}\right)_{3}=\left({\frac {\alpha }{\pi _{1}}}\right)_{3}^{{\nu _{1}}}\left({\frac {\alpha }{\pi _{2}}}\right)_{3}^{{\nu _{2}}}\cdots \;,\,$ es eine Zerlegung $\lambda =\pi _{1}^{{\nu _{1}}}\pi _{2}^{{\nu _{2}}}\pi _{3}^{{\nu _{3}}}\dots$ von $\lambda$ in paarweise verschiedene Primelemente $\pi _{j}$ hat, von denen keines zu $1-\omega$ assoziiert ist.

Ist der „Zähler“ $\alpha$ ein kubischer Rest modulo $\lambda$ und $\lambda \not \equiv 0{\pmod {1-\omega }}$ , dann nimmt das Symbol den Wert 1 an.
Nimmt das Symbol einen von 1 verschiedenen Wert an, dann ist der Zähler kein kubischer Rest modulo $\lambda$ oder $\lambda$ nicht teilerfremd zu 3.
Das Symbol kann den Wert 1 annehmen, auch wenn der Zähler ein kubischer Nichtrest modulo $\lambda$ ist.

Primäre Zahlen

Zur Formulierung eines kubischen Reziprozitätsgesetzes auf dem Ring der Eisenstein-Zahlen müssen aus den Assoziierten einer Eisensteinzahl bestimmte Vertreter ausgewählt werden. Eisenstein nennt eine Zahl $\lambda$ primär, wenn sie die Kongruenz $\lambda \equiv 2{\pmod 3}$ erfüllt. Man kann leicht nachweisen, dass für Zahlen, deren Norm (in $\mathbb {Z}$ ) teilerfremd zu 3 ist, genau ein zu ihnen assoziiertes Element primär im Sinne dieser Definition ist. Ein Nachteil der Definition ist, dass das Produkt zweier primärer Zahlen immer die Gegenzahl einer primären Zahl ist.

Man definiert daher heute meistens:

Eine Eisenstein-Zahl $\lambda$ ist primär, wenn sie zu 3 teilerfremd ist und modulo $(1-\omega )^{2}=-3\omega$ zu einer gewöhnlichen ganzen Zahl kongruent ist.

Diese Definition ist gleichbedeutend damit, dass die Kongruenz $\lambda \equiv \pm 1{\pmod 3}$ im Ring der Eisensteinzahlen gilt. Es gilt dann:

Falls die Norm von $\lambda \in \mathbb{Z } [\omega ]^{*}$ teilerfremd zu 3 ist, dann ist genau eine der Zahlen $\lambda ,\omega \cdot \lambda ,\omega ^{2}\cdot \lambda$ primär.
Das Produkt von zwei primären Zahlen ist primär.
Mit jeder Zahl ist auch die zu ihr konjugiert komplexe Zahl primär.
Eine im modernen Sinn primäre Zahl $\lambda$ ist entweder selbst primär im Sinn von Eisenstein oder $-\lambda$ ist es.
Unter den Assoziierten einer Zahl, die teilerfremd zu 3 ist, sind stets genau zwei primäre Zahlen $\pm \lambda$ .

Da −1 immer ein kubischer Rest ist, reicht die Eindeutigkeit dieser Definition „bis auf das Vorzeichen“ für die Formulierung des Reziprozitätsgesetzes aus.

Kubisches Reziprozitätsgesetz

Für zwei primäre Zahlen $\alpha,\beta$ gilt:

$\left({\frac {\alpha }{\beta }}\right)_{3}=\left({\frac {\beta }{\alpha }}\right)_{3}$

Zu diesem kubischen Reziprozitätsgesetz gibt es Ergänzungssätze für die Einheiten und das Primelement $1-\omega$ :

Falls $\lambda =a+b\omega ,(a,b\in \mathbb{Z } )$ primär ist und $a=3m+1,b=3n,(m,n\in \mathbb{Z } )$ gilt, dann gilt auch

$\left({\frac {\omega }{\lambda }}\right)_{3}=\omega ^{{\frac {1-a-b}{3}}}=\omega ^{{-m-n}},\;\;\;\left({\frac {1-\omega }{\lambda }}\right)_{3}=\omega ^{{\frac {a-1}{3}}}=\omega ^{m},\;\;\;\left({\frac {3}{\lambda }}\right)_{3}=\omega ^{{\frac {b}{3}}}=\omega ^{n}.$

Für primäre „Nenner“ $\lambda$ mit $a\equiv 2{\pmod 3}$ kann $\lambda$ durch das assoziierte primäre Element $-\lambda$ ersetzt werden, ohne dass sich der Wert des Symbols ändert.

Basierend auf einem Artikel in:

Wikipedia.de