Parkettierung
In der Mathematik bezeichnet Parkettierung (auch Kachelung, Pflasterung oder Flächenschluss) die lückenlose und überlappungsfreie Überdeckung der (euklidischen) Ebene durch gleichförmige Teilflächen. Das Konzept kann auch auf höhere Dimensionen erweitert werden.
Bei praktischen Anwendungen wird die Überdeckung mit Hilfe von Primitiven („primitiven“ Flächen-Formen, möglichst mit einem einfachen Polygon) bevorzugt, wofür der entsprechend einschränkende Begriff Tessellation (englisch für „Mosaik“) verwendet wird. Wenn in einer technischen Anwendung ein großes Blech in nicht-primitive Teilflächen (Werkstücke) aufzuteilen ist, wird versucht, diese so zu gestalten, dass eine Parkettierung durch ungleiche Teilflächen vorliegt und kein Abfall entsteht.
Die „zyklische Aufteilung von Flächen“ mit ungleichförmigen Teilflächen (keine Polygone) in der Kunst kommt sehr ausgeprägt bei M. C. Escher vor.
Analog zur Parkettierung beziehungsweise zur Tessellation der Ebene (2D) kann auch der drei- oder höherdimensionale Raum unterteilt werden, siehe Raumfüllung.
Definitionen
Eine Kachel (Parkettstein, Pflasterstein) ist eine abgeschlossene topologische Scheibe in der Ebene. (Dadurch werden u.a. Steine mit Löchern und nicht-zusammenhängenden Teilen ausgeschlossen. Gelegentlich werden aber auch solche und allgemeinere Steine zugelassen.)
Eine Parkettierung (Pflasterung, Kachelung, manchmal auch Mosaik) ist eine (abzählbare) Menge von Kacheln, welche sowohl eine Packung (d.h., „kein Punkt der Ebene liegt im Inneren von zwei oder mehr Kacheln“, oder, anders ausgedrückt, „verschiedene Kacheln haben höchstens Randpunkte gemeinsam“) als auch eine Überdeckung (d.h., „jeder Punkt der Ebene gehört zu mindestens einer Kachel“) ist.
Häufig schränkt man den Begriff noch weiter ein, indem man z.B. fordert, dass alle Kacheln homöomorph zur abgeschlossenen Kreisscheibe sind (damit insbesondere kompakt und einfach zusammenhängend), oder aber, dass jede Kachel kongruent zu einem Element einer endlichen Auswahl von Kacheln (den sogenannten „Proto-Kacheln“) ist, dass also nur endlich viele verschiedene Kacheln auftreten. Gibt es genau eine Protokachel, so heißt die Parkettierung monohedral. Dabei fordert man zwar, dass die Kacheln untereinander kongruent sind, zur Protokachel, die die Parkettierung charakterisiert, jedoch nur ähnlich. Gibt es zu einer Form (Protokachel) eine (monohedrale) Parkettierung der Ebene, sagt man auch kurz „die Protokachel parkettiert“.
Periodische Parkettierungen

Eine Kongruenzabbildung
(euklidische Bewegung) der Ebene, welche jede Kachel einer Parkettierung wieder
auf eine Kachel abbildet, heißt „Symmetrie“ der Parkettierung. Die Menge aller
Symmetrien heißt Symmetriegruppe
(der Parkettierung). Sie ist eine Untergruppe
der Gruppe
der euklidischen Bewegungen der Ebene. Enthält die Symmetriegruppe einer
Parkettierung zwei linear
unabhängige Verschiebungen, so heißt die Parkettierung „periodisch“ und die
entstehende Symmetriegruppe ebene
kristallographische Gruppe von denen es genau 17, die sogenannten
Tapetenmustergruppen, gibt.
Wenn man gewisse Anforderungen an die in einer Parkettierung verwendeten Grundformen und ihre Anordnung stellt, ergeben sich Spezialfälle, für die man dann alle möglichen Parkettierungen angeben kann.
Platonische Parkettierungen
Ist nur ein regelmäßiges Polygon als Kachel zugelassen und wird weiter eingeschränkt, dass die Kacheln Kante an Kante angeordnet werden müssen, ergeben sich genau drei mögliche Parkettierungen der Ebene, die platonischen oder regulären Parkettierungen:
Johannes Kepler war der erste, der diese Parkettierungen untersuchte und erkannte, dass sie ein Analogon zu den regulären Polyedern darstellen.
-
 Dreiecksgitter
Dreiecksgitter -
 Quadratgitter
Quadratgitter -
 Sechseckgitter – wird auch Bienenwabenmuster genannt
Sechseckgitter – wird auch Bienenwabenmuster genannt
Archimedische Parkettierungen
Dürfen als Grundform beliebige regelmäßige n-Ecke mit gleicher Kantenlänge verwendet werden, so ergeben sich bei Beibehaltung der Kante-an-Kante-Regel und der Einschränkung, dass an jedem Punkt, an dem die Ecken zusammenstoßen, immer die gleiche Kombination von Vielecken (Anzahl und Reihenfolge) zusammenstoßen muss, genau acht weitere mögliche Parkettierungen – die archimedischen, semiregulären oder 1-uniformen Parkettierungen der Ebene:
- 2 Parkettierungen aus Dreiecken und Quadraten
- 2 Parkettierungen aus Dreiecken und Sechsecken
- 1 Parkettierung aus Dreiecken, Quadraten und Sechsecken
- 1 Parkettierung aus Dreiecken und Zwölfecken
- 1 Parkettierung aus Achtecken und Quadraten
- 1 Parkettierung aus Quadraten, Sechsecken und Zwölfecken
-
 3-3-3-4-4
3-3-3-4-4 -
 3-3-4-3-4
3-3-4-3-4 -
 3-6-3-6
3-6-3-6 -
 3-3-3-3-6 (zwei gespiegelte Varianten)
3-3-3-3-6 (zwei gespiegelte Varianten) -
 3-4-6-4
3-4-6-4 -
 3-12-12
3-12-12 -
 4-8-8
4-8-8 -
 4-6-12
4-6-12
Demireguläre Parkettierungen
Parkettierungen, für die zwar als Grundform beliebige regelmäßige n-Ecke mit gleicher Kantenlänge verwendet werden und die die Kante-an-Kante-Regel einhalten, bei denen aber an den Punkten, an denen die Ecken zusammenstoßen, eine von zwei möglichen Kombinationen von Vielecken (Anzahl und Reihenfolge) auftritt, nennt man demireguläre oder 2-uniforme Parkettierungen, zum Beispiel:
- Parkettierung aus Dreiecken und Quadraten (anderes Muster als bei den entsprechenden archimedischen Parketten)
- Parkettierung aus Dreiecken und Sechsecken (anderes Muster als bei den entsprechenden archimedischen Parketten)
- Parkettierung aus Dreiecken, Quadraten und Sechsecken (anderes Muster als bei den entsprechenden archimedischen Parketten)
- Parkettierung aus Dreiecken, Quadraten und Zwölfecken
- Parkettierung aus Dreiecken, Quadraten, Sechsecken und Zwölfecken
Es gibt insgesamt 20 demireguläre Parkettierungen.
-
 3-3-4-3-4 und 3-3-3-3-3-3 (Typ 1)
3-3-4-3-4 und 3-3-3-3-3-3 (Typ 1) -
 3-3-4-3-4 und 3-3-3-3-3-3 (Typ 2)
3-3-4-3-4 und 3-3-3-3-3-3 (Typ 2) -
 3-3-6-6 und 3-3-3-3-3-3
3-3-6-6 und 3-3-3-3-3-3 -
 3-3-6-6 und 3-6-3-6
3-3-6-6 und 3-6-3-6 -
 3-4-4-6 und 3-6-3-6
3-4-4-6 und 3-6-3-6 -
 3-3-4-12 und 3-3-3-3-3-3
3-3-4-12 und 3-3-3-3-3-3
Parkettierungen mit unregelmäßigen Polygonen
Parkettierungen sind auch mit unregelmäßigen Polygonen möglich. Beispiele sind:
- Parkettierung mit Fünfecken, wie das Cairo tiling
- Parkettierung mit Sechsecken und Fünfecken, wie die Grazebrook-Parkettierung
Der niederländische Künstler M. C. Escher ist bekannt für seine Parkettierungen mit exotischen Figuren.
-
 Rauten mit je zwei 60°-Winkeln und je zwei 120°-Winkeln
Rauten mit je zwei 60°-Winkeln und je zwei 120°-Winkeln -
 Deltoide mit je zwei rechten Winkeln und je einem von der Symmetrieachse geschnittenen 60°-Winkel
Deltoide mit je zwei rechten Winkeln und je einem von der Symmetrieachse geschnittenen 60°-Winkel -
 Bisher bekannte 15 Arten der Parkettierung mit Fünfecken
Bisher bekannte 15 Arten der Parkettierung mit Fünfecken
Isohedrale Parkettierungen und anisohedrale Kacheln
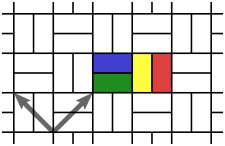
Eine monohedrale Parkettierung heißt isohedral, wenn es zu je zwei Kacheln der Parkettierung eine Kongruenzabbildung gibt, die die eine Kachel auf die andere abbildet. In der Abbildung 2 kann das grüne in das blaue Rechteck durch eine Punktspiegelung am Mittelpunkt der gemeinsamen Seite, das grüne in das gelbe Rechteck durch eine Drehung um den gemeinsamen Eckpunkt und das grüne in das rote Rechteck durch eine Kombination von beidem überführt werden. In die Nähe der bunten Rechtecke kommt man durch Parallelverschiebung, wie durch die grauen Pfeile angedeutet.
In diesem Fall, wenn also die Gruppe der Kongruenzabbildungen transitiv
auf der Parkettierung operiert, besteht die Parkettierung auch aus einer
einzigen Bahn.
Ist
die Anzahl der Bahnen, dann wird die Parkettierung
-isohedral
genannt.
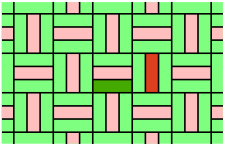

In der Parkettierung der Abbildung 3 gibt es keine Kongruenzabbildung, die
das dunkelgrüne Rechteck in das dunkelrote überführt. Die Parkettierung besteht
aus zwei Bahnen, den grünlichen und den rötlichen Rechtecken, und ist damit
2-isohedral. Ist ,
wird die Parkettierung gelegentlich auch anisohedral genannt. Bei einer
Kachel sagt man, sie ist
-anisohedral,
oder, sie hat die isohedrale Zahl
(engl. isohedral number), wenn sie parkettiert und
-isohedral
ist, aber nicht
-isohedral
für
.
So gesehen hat das (3:1)-Rechteck der
Abbildung 3 die isohedrale Zahl 1, da es mit ihm natürlich auch isohedrale
Parkettierungen gibt.
Es gibt aber auch Kacheln, die zwar parkettieren, zu denen es aber überhaupt keine transitive Parkettierung geben kann. Ein Beispiel ist der Pflasterstein von Heinrich Heesch (siehe Abbildung 4), bei dem nach der Gegebenheit der grünen und blauen Kacheln die (gespiegelten) gelben und roten zwar für die Parkettierung erforderlich sind, es aber keine Kongruenzabbildung gibt, die grüne oder blaue Kacheln in gelbe bzw. rote überführen würde. Bspw. können durch eine Achsenspiegelung grüne oder blaue Kacheln in gelbe bzw. rote überführt werden, die Bilder der gelben und/oder roten erfahren dabei aber einen Versatz um 2 Raster, so dass sie nicht mit grünen oder blauen Kacheln zur Deckung zu bringen sind.
Aperiodische Parkettierungen
Sätze von Proto-Kacheln (s.o.), die ausschließlich nichtperiodische Überdeckungen der Ebene zulassen, heißen aperiodisch oder quasikristallin. Parkettierungen können quasiperiodisch sein, das heißt, dass sich beliebig große Ausschnitte wiederholen, ohne dass das Parkett insgesamt periodisch ist. Interessante und schöne Beispiele für quasiperiodische Parkettierungen sind die Penrose-Parkettierungen, benannt nach ihrem Entdecker Roger Penrose.
-
.svg.png) P1-Parkettierung
P1-Parkettierung -
 P2-Parkettierung
P2-Parkettierung -
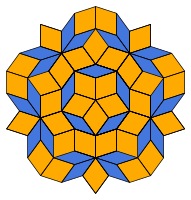 P3-Parkettierung
P3-Parkettierung
Literatur
- Hans-Günther Bigalke, Heinrich Wippermann: Reguläre Parkettierungen, BI-Wissenschafts-Verlag 1994, ISBN 3-411-16711-4
- Bruno Ernst: Der Zauberspiegel des M. C. Escher, Taschen, 1992, ISBN 3-8228-0442-8
- Heinrich Heesch, Otto Kienzle: Flächenschluß, Springer, 1963
- Branko Grünbaum, G. C. Shephard: Tilings and Patterns. WH Freeman & Co., 1986, ISBN 0-7167-1193-1


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.06. 2021