
A4 (Gruppe)
Die
(alternierende
Gruppe 4. Grades) ist eine bestimmte 12-elementige Gruppe, die im mathematischen
Teilgebiet der Gruppentheorie
untersucht wird. Sie steht in enger Beziehung zur symmetrischen
Gruppe
,
es handelt sich bei der
um die Untergruppe, die aus allen geraden
Permutationen besteht. Geometrisch entsteht die
als Gruppe der Drehungen des regelmäßigen Tetraeders
auf sich.
Geometrische Einführung
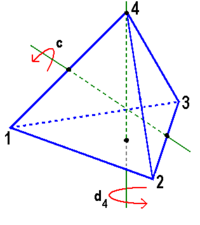
Betrachtet man die Drehungen, die ein regelmäßiges Tetraeder in sich selbst überführen, so findet man 12 Möglichkeiten:
- die Identität
,
- drei Drehungen um 180° um Achsen, die durch die Mittelpunkte zweier gegenüberliegender Kanten verlaufen,
- vier Drehungen um 120° um Höhen des Tetraeders,
- vier Drehungen um 240° um Höhen des Tetraeders.
Spiegelungen werden hier nicht betrachtet. Für die Drehungen wählen wir die folgenden Bezeichnungen:
ist die Drehung um 180° um die Gerade, die durch die Mittelpunkte der Kanten 12 und 34 läuft (1,2,3 und 4 bezeichnen Tetraederecken wie in nebenstehender Zeichnung).
ist die Drehung um 180° um die Gerade, die durch die Mittelpunkte der Kanten 13 und 24 läuft.
ist die Drehung um 180° um die Gerade, die durch die Mittelpunkte der Kanten 14 und 23 läuft.
sei die Drehung um 120° um die durch die Ecke
verlaufende Höhe, und zwar im positiven Drehsinn (das heißt im Gegenuhrzeigersinn) von der durchstoßenen Ecke aus gesehen.
sei die Drehung um 240° um die durch die Ecke
verlaufende Höhe, ebenfalls mit dem oben angegebenen Drehsinn.
Diese Drehungen lassen sich durch Hintereinanderausführung
kombinieren, wodurch man wieder eine Drehung aus obiger Liste erhält. Man
schreibt einfach zwei Drehungen (oft ohne Verknüpfungszeichen, oder mit
oder
)
nebeneinander und meint damit, dass zuerst die rechtsstehende und dann die
linksstehende Drehung auszuführen ist. Die Schreibweise
macht bereits deutlich, dass die Drehung um 240° gleich der zweifachen
Hintereinanderausführung der Drehung um 120° ist.
Man erhält auf diese Weise die 12-elementige Gruppe
aller Drehungen des regelmäßigen Tetraeders auf sich.
Trägt man alle so gebildeten Verknüpfungen in eine Verknüpfungstafel ein, so erhält man
Darstellung als Permutationsgruppe
Die oben beschriebenen Drehungen sind bereits dadurch festgelegt, wie die mit
1,2,3 und 4 bezeichneten Ecken aufeinander abgebildet werden. Jedes Element der
kann daher als Permutation der Menge
aufgefasst werden. Verwendet man die übliche Zweizeilenform
und die Zykelschreibweise,
so erhält man:
Man sieht hier mit einem Blick, dass jedes Element der
als ein Produkt aus einer geraden Anzahl von Transpositionen (=
Zweierpermutationen) geschrieben werden kann. Die zugehörigen Permutationen
nennt man ebenfalls gerade, das heißt die
besteht genau aus den geraden Permutationen der Menge
.
Damit tritt die
als Kern
der Signum-Abbildung:
auf, wobei
die symmetrische
Gruppe vierten Grades ist.
Eigenschaften
Untergruppen
Sämtliche Untergruppen der
sind in nebenstehender Zeichnung angegeben.
ist zur Kleinschen
Vierergruppe isomorph. Gemäß dem Satz
von Lagrange teilt die Ordnung
einer jeden Untergruppe die Gruppenordnung, in diesem Falle 12. Umgekehrt muss
es aber nicht zu jedem Teiler der Gruppenordnung eine Untergruppe dieser Ordnung
geben. Die
ist ein Beispiel für dieses Phänomen, denn sie hat keine Untergruppe der Ordnung
6.
Normalteiler, Auflösbarkeit
Die
ist nicht abelsch,
denn
ist aber auflösbar,
wie die Reihe
zeigt. Das Zeichen
bedeutet “ist Normalteiler in”.
ist die Kommutatorgruppe
von
,
insbesondere also ein Normalteiler
und es gilt
Die zwei- und dreielementigen Untergruppen sind keine Normalteiler.
Semidirektes Produkt
Da
und
teilerfremde
Gruppenordnungen haben, folgt aus dem Satz
von Schur-Zassenhaus, dass die
zum semidirekten
Produkt
isomorph ist, wobei
die Restklasse
auf den Automorphismus
abbildet.
Erzeuger und Relationen
Man kann Gruppen auch dadurch beschreiben, dass man ein Erzeugendensystem und Relationen, die die Erzeuger erfüllen müssen, angibt. Erzeuger und Relationen notiert man, durch das Zeichen | getrennt, in spitzen Klammern. Die Gruppe ist dann die von den Erzeugern erzeugte freie Gruppe modulo dem von den Relationen erzeugten Normalteiler. In diesem Sinne ist:
Man sieht leicht, dass
und
die Relationen erfüllen und dass
und
die gesamte Gruppe erzeugen, was für den Beweis aber noch nicht ausreicht.
Charaktertafel
Die Charaktertafel
der
sieht wie folgt aus:
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 01.01. 2020