
Stetige Funktion
In der Mathematik ist eine
stetige Abbildung oder stetige Funktion eine Funktion, bei der
hinreichend kleine Änderungen des Arguments nur beliebig kleine Änderungen des
Funktionswerts nach sich ziehen. Formalisieren kann man diese Eigenschaft mit
der Vertauschbarkeit der Funktion mit Grenzwerten oder mit dem -
-Kriterium.
Anschaulich gesprochen ist eine reelle stetige Funktion
dadurch gekennzeichnet, dass ihr Graph in einem kartesischen
Koordinatensystem innerhalb ihres Definitionsbereiches eine zusammenhängende
Kurve ist, der Graph also keine Sprünge macht und man ihn ohne Absetzen des
Stiftes zeichnen kann.
Viele in der Praxis der reellen Analysis verwendete Funktionen sind stetig, insbesondere ist das für alle differenzierbaren Funktionen der Fall.
Für stetige Funktionen können eine Reihe nützlicher Eigenschaften bewiesen werden. Exemplarisch seien der Zwischenwertsatz, der Satz vom Minimum und Maximum und der Fundamentalsatz der Analysis genannt.
Allgemeiner ist das Konzept der Stetigkeit von Abbildungen in der Mathematik vor allem in den Teilgebieten der Analysis und der Topologie von zentraler Bedeutung. Es ist möglich, Stetigkeit durch eine Bedingung zu charakterisieren, die nur Begriffe der Topologie benutzt. Somit kann der Begriff der Stetigkeit auch auf Funktionen zwischen topologischen Räumen ausgedehnt werden. Diese allgemeine Sichtweise erweist sich aus mathematischer Sicht als der „natürlichste“ Zugang zum Stetigkeitsbegriff: Stetige Funktionen sind diejenigen Funktionen zwischen topologischen Räumen, die mit deren Strukturen „verträglich“ sind. Stetige Funktionen spielen also in Topologie und Analysis eine ähnliche Rolle wie Homomorphismen in der Algebra.
Motivation

Die Funktion
„springt“ an der Stelle
vom Funktionswert 1 auf den Funktionswert 2. Stellt die Funktion einen
Zusammenhang aus der Natur oder der Technik dar, so erscheint ein solches
Verhalten als unerwartet (Natura
non facit saltus). Beschreibt die Funktion zum Beispiel den Zusammenhang
zwischen der beim Radfahren aufgebrachten Energie und der erreichten
Geschwindigkeit, so wäre es überraschend, wenn eine minimale Steigerung der
aufgewandten Energie an einer Stelle sprunghaft zur Verdoppelung der
Geschwindigkeit führte.
Der mathematische Begriff der Stetigkeit versucht die Funktionen exakt zu
beschreiben, die ein solches „willkürliches“ Verhalten nicht haben. Die
angegebene Funktion
ist also nicht stetig, wobei sich die Unstetigkeit auf den Punkt
einschränken lässt. In allen anderen Punkten ist die Funktion stetig.
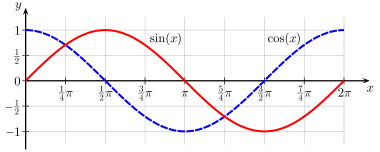
Anschaulich wird Stetigkeit oft damit assoziiert, den Graphen einer Funktion in einem Zug ohne Absetzen zeichnen zu können. Diese Anschauung stößt an gewisse Grenzen, besonders wenn man Funktionen mit anderen Definitionsbereichen als der gesamten reellen Zahlengerade betrachtet. Deshalb werden mathematisch exakte Definitionen benötigt.
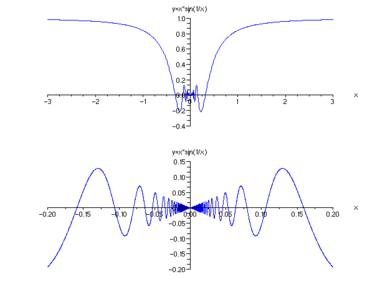
Beispielsweise ist die durch
gegebene Funktion anschaulich stetig, denn außer bei
ist ihr Graph eine durchgehende Linie, und bei
hat er keinen Platz, „Sprünge“ zu machen. Ob er sich aber bis zum Nullpunkt
„ohne Absetzen zeichnen lässt“, kann man nicht ohne eine genauere Definition
dessen entscheiden, was eine erlaubte Zeichnung sein soll. Da ist es einfacher,
eine Definition von „stetig“ ohne den Begriff „zeichnen“ zu entwickeln, nach der
diese Funktion als stetig nachgewiesen werden kann. Dann können durchaus die
eben genannten Gründe zum Beweis beitragen.
Die Funktion
Stetigkeit reeller Funktionen
Definition
Sei
eine reelle
Funktion, also eine Funktion
,
deren Funktionswerte reelle
Zahlen sind und deren Definitionsbereich
ebenfalls aus reellen Zahlen besteht.
In der reellen Analysis gibt es mehrere
gleichwertige Möglichkeiten, die Stetigkeit von
in einem
zu definieren. Die gebräuchlichsten sind das Epsilon-Delta-Kriterium und die
Definition mittels Grenzwerten.
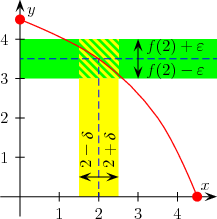
Definition mittels Epsilon-Delta-Kriterium.
heißt stetig in
,
wenn zu jedem
ein
existiert, so dass für alle
mit
gilt:
.
Intuitiv bedeutet die Bedingung der Stetigkeit, dass zu jeder Änderung
des Funktionswertes, die man zu akzeptieren bereit ist, eine maximale Änderung
im Argument gefunden werden kann, die diese Vorgabe sicherstellt.
Seien
und
mit
.
Es ist
.
Damit dies kleiner als die vorgegebene Zahl
ist, kann z.B.
gewählt werden. Denn aus
folgt dann nämlich
.
Bemerkungen:
- Da die Funktion
an jeder Stelle
stetig ist, ist
somit auf ganz
stetig.
- Weil
lediglich von
, nicht aber von der Stelle
abhängt, ist
sogar auf ganz
gleichmäßig stetig.
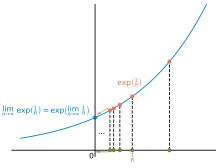
Definition mittels Grenzwerten. Bei dieser Definition fordert man die
Vertauschbarkeit von Funktionsausführung und Grenzwertbildung. Hierbei kann man
sich wahlweise auf den Grenzwertbegriff für
Funktionen oder für
Folgen stützen.
Im ersten Fall formuliert man:
heißt stetig in
,
wenn der Grenzwert
existiert und mit dem Funktionswert
übereinstimmt, wenn also gilt:
.
Im zweiten Fall formuliert man:
heißt stetig in
,
wenn für jede gegen
konvergente Folge
mit Elementen
,
die Folge
gegen
konvergiert.
Die zweite Bedingung wird auch als Folgenkriterium
bezeichnet.
Statt von Stetigkeit in
spricht man oft auch von Stetigkeit im Punkt
oder Stetigkeit an der Stelle
.
Ist diese Bedingung nicht erfüllt, so nennt man
unstetig in (im Punkt/an der Stelle)
,
bzw. bezeichnet
als Unstetigkeitsstelle von
.
Man spricht von einer stetigen Funktion, wenn die Funktion in jedem Punkt ihres Definitionsbereiches stetig ist.
Beispiele stetiger und unstetiger Funktionen
Ist eine Funktion an einer Stelle differenzierbar, so ist sie dort auch stetig. Damit folgt insbesondere die Stetigkeit
- aller rationalen
Funktionen (also etwa
oder
)
- der Exponentialfunktionen
, für festes
- der trigonometrischen Funktionen (also Sinus, Kosinus, Tangens,…)
- der Logarithmusfunktionen
Die Stetigkeit dieser Funktionen lässt sich aber auch ohne Rückgriff auf den Begriff der Differenzierbarkeit direkt beweisen.
Die Betragsfunktion
ist ebenfalls stetig, auch wenn sie im Punkt 0 nicht differenzierbar ist.
Ebenfalls stetig sind alle Potenzfunktionen
(etwa ),
obwohl sie für einen Exponenten kleiner 1 im Punkt 0 ebenfalls nicht
differenzierbar sind.
Tatsächlich sind alle elementaren
Funktionen stetig (zum Beispiel ).
Bei der Betrachtung der elementaren Funktionen ist allerdings zu beachten,
dass einige elementare Funktionen als Definitionsbereich nur eine echte
Teilmenge der reellen Zahlen haben. Bei der Quadratwurzelfunktion werden
z.B. alle negativen Zahlen ausgelassen, bei der Tangensfunktion alle
Nullstellen des Kosinus.
In diesen Fällen wird manchmal unpräzise formuliert,
die Funktionen seien in den entsprechenden Stellen unstetig. Dies ist allerdings
nicht richtig, da sich die Frage nach der Stetigkeit nur für Punkte im
Definitionsbereich stellt. Mathematisch sinnvoll ist allerdings die Frage nach
einer stetigen
Fortsetzung der Funktion an einer Definitionslücke.
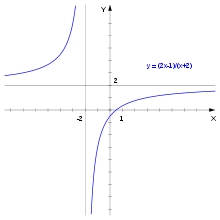
Beispielsweise ist die Funktion
definiert für alle reellen Zahlen
und in jedem Punkt ihres Definitionsbereiches stetig. Sie ist also eine stetige
Funktion. Die Frage der Stetigkeit in
stellt sich nicht, weil dieser Punkt nicht zum Definitionsbereich gehört. Eine
stetige Fortsetzung der Funktion an dieser Definitionslücke ist nicht möglich.
Die Betrags- und die Wurzelfunktion sind Beispiele stetiger Funktionen, die an einzelnen Stellen des Definitionsbereichs nicht differenzierbar sind. Die mathematische Fachwelt nahm noch Anfang des 19. Jahrhunderts an, dass eine stetige Funktion zumindest an "den meisten" Stellen differenzierbar sein müsse. Bernard Bolzano konstruierte dann als erster Mathematiker eine Funktion, die überall stetig, aber nirgends differenzierbar ist, die Bolzanofunktion. Er veröffentlichte sein Resultat allerdings nicht. Karl Weierstraß fand dann in den 1860er Jahren ebenfalls eine derartige, als Weierstraß-Funktion bekannte Funktion, womit er in der mathematischen Fachwelt Aufsehen erregte. Der Graph der Weierstraß-Funktion kann effektiv nicht gezeichnet werden. Dies zeigt, dass die intuitive Erklärung, eine stetige Funktion sei eine Funktion, deren Graph sich ohne Absetzen des Stiftes zeichnen lässt, in die Irre führen kann. Letztlich muss man bei der Untersuchung der Eigenschaften stetiger Funktionen immer auf die exakte Definition zurückgreifen.
Mit Methoden der Mathematik des 20. Jahrhunderts konnte sogar gezeigt werden, dass die Funktionen, die nirgends differenzierbar sind, in gewissem Sinne "häufig" unter den stetigen Funktionen sind.
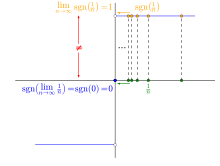
Einfache Beispiele unstetiger Funktionen sind:
- die Vorzeichenfunktion (unstetig nur in 0)
- die Dirichlet-Funktion (in jedem Punkt unstetig)
- die thomaesche Funktion (unstetig genau in allen rationalen Zahlen).
Stetigkeit zusammengesetzter Funktionen
Ähnlich wie die Differenzierbarkeit ist die Stetigkeit eine Eigenschaft, die
sich bei vielen Operationen von den Bestandteilen auf die daraus
zusammengesetzten Funktionen überträgt. Bei den folgenden Punkten sei die
Stetigkeit von
in
bereits gegeben.
- Hintereinanderausführung: Ist
eine weitere reelle Funktion, deren Definitionsbereich den Wertebereich von
umfasst und die in
stetig ist, dann ist die Komposition
stetig in
.
- Algebraische Operationen: Ist
eine weitere reelle Funktion mit dem selben Definitionsbereich wie
, die ebenfalls in
stetig ist, dann sind die punktweise definierten Funktionen
,
,
und
ebenfalls stetig in
. Im letzten Fall ist allerdings zu beachten, dass der Definitionsbereich der zusammengesetzten Funktion sich als
ohne die Nullstellenmenge von
ergibt. Insbesondere darf
selbst in diesem Fall also keine Nullstelle von
sein.
- Maximum/Minimum: Unter den gleichen Voraussetzungen wie im vorherigen
Punkt sind die punktweise definierten Funktionen
und
stetig in
.
Passen die Definitionsbereiche der beteiligten Funktionen nicht wie gefordert zusammen, so kann man sich eventuell durch geeignete Einschränkungen der Definitionsbereiche weiter helfen.
Unter bestimmten Voraussetzungen überträgt sich Stetigkeit auch auf die Umkehrfunktion. Allerdings kann die Aussage hier nicht für die punktweise Stetigkeit formuliert werden:
- Ist der Definitionsbereich der injektiven,
stetigen reellen Funktion
ein Intervall, so ist die Funktion streng monoton (steigend oder fallend). Die auf dem Wertebereich von
definierte Umkehrfunktion
ist ebenfalls stetig.
Mit Hilfe dieser Permanenzeigenschaften kann man zum Beispiel die Stetigkeit
der oben angegebenen elementaren Funktion
aus der Stetigkeit des Kosinus, der identischen
Funktion und der konstanten
Funktionen ableiten. Verallgemeinert man diese Überlegung, so ergibt sich
die Stetigkeit aller elementaren Funktionen als Konsequenz aus den vorher
angegebenen einfachen Beispielen.
Hauptsätze über stetige reelle Funktionen
Es gibt eine Reihe wichtiger Sätze, die für stetige reelle Funktionen
gelten. Diese lassen sich am einfachsten formulieren, wenn man annimmt, dass
mit
ein abgeschlossenes, beschränktes Intervall ist:
- Zwischenwertsatz:
Die Funktion nimmt jeden Wert zwischen
und
an.
- Satz
vom Minimum und Maximum:
ist beschränkt und Infimum und Supremum seiner Funktionswerte werden auch als Funktionswert angenommen. Es handelt sich also tatsächlich um Minimum und Maximum. Dieser von Weierstraß bewiesene Satz, bisweilen auch Extremwertsatz genannt, liefert nur die Existenz dieser Extremwerte. Für ihr praktisches Auffinden sind häufig Aussagen aus der Differentialrechnung nötig.
- Fundamentalsatz
der Analysis:
ist Riemann-integrierbar und die Integralfunktion
-
- ist eine Stammfunktion
von
.
- Satz
von Heine:
erfüllt eine strengere Version des Epsilon-Delta-Kriteriums. Die entsprechende Eigenschaft wird gleichmäßige Stetigkeit genannt.
Aus Zwischenwertsatz und Satz vom Minimum und Maximum zusammen folgt, dass
das Bild
von
ebenfalls ein abgeschlossenes, beschränktes
Intervall
(bzw. im Fall einer konstanten Funktion eine einpunktigen Menge) ist.
Andere Stetigkeitsbegriffe
Verschärfungen des Begriffs der Stetigkeit sind z.B. gleichmäßige Stetigkeit, (lokale) Lipschitz-Stetigkeit, Hölder-Stetigkeit sowie die absolute Stetigkeit und die geometrische Stetigkeit. Die gewöhnliche Stetigkeit wird mitunter auch als punktweise Stetigkeit bezeichnet, um sie gegenüber der gleichmäßigen Stetigkeit abzugrenzen. Anwendungen der Lipschitz-Stetigkeit finden sich z.B. in Existenz- und Eindeutigkeitssätzen (z.B. Satz von Picard-Lindelöf) für Anfangswertprobleme gewöhnlicher Differentialgleichungen und in der geometrischen Maßtheorie. Die absolute Stetigkeit findet Verwendung in der Stochastik und der Maßtheorie, die geometrische Stetigkeit in der geometrischen Modellierung.
Eine Eigenschaft, die eine Menge von Funktionen besitzen kann, ist die gleichgradige Stetigkeit. Sie spielt eine Rolle im häufig verwendeten Satz von Arzelà-Ascoli.
Stetigkeit für Funktionen mehrerer Variablen
Eine Funktion
heißt stetig in ,
wenn für jede gegen
konvergierende Folge die Folge der Funktionswerte gegen
konvergiert.
Sie heißt stetig, wenn sie in jedem Punkt des Definitionsbereichs stetig ist.
Ist die Funktion
stetig, so ist sie auch stetig in jedem Argument.
Dabei heißt die Funktion
stetig im ersten Argument, wenn für jedes
die Funktion
stetig ist. Analog wird die Stetigkeit im zweiten, dritten, … , -ten
Argument definiert.
.png)
Umgekehrt folgt aus der Stetigkeit in jedem Argument noch nicht die
Stetigkeit von ,
wie das folgende Beispiel zeigt:
Man überzeugt sich leicht, dass diese Funktion in beiden Argumenten stetig
ist. Die Funktion ist im Punkt
aber unstetig. Definiert man nämlich
für
,
so ist
eine Folge, die in
gegen
konvergiert. Es gilt
für alle
.
Die Bildfolge hat also den konstanten Wert
und konvergiert somit nicht gegen den Funktionswert 0 an der betrachteten
Stelle.
Stetigkeit für Abbildungen zwischen metrischen Räumen
Definition
Seien
und
metrische Räume,
eine Abbildung und
.
Dann heißt
stetig in
,
wenn aus
stets
folgt. Diese Bedingung ist wieder äquivalent zum
Kriterium.
Die Abbildung
heißt stetig, wenn sie in jedem Punkt
stetig ist.
Abbildungen zwischen endlich-dimensionalen euklidischen Vektorräumen
Eine Abbildung
ist im Sinne dieser Definition genau dann stetig in ,
wenn die Komponentenabbildungen
alle stetig in
sind.
Abbildungen zwischen normierten Vektorräumen
zwischen normierten
Vektorräumen ist genau dann stetig, wenn er beschränkt
ist, wenn es also eine Konstante
gibt, so dass
für alle .
Diese Charakterisierung gilt allgemeiner auch für Abbildungen zwischen
bornologischen
Räumen.
Sind
und
sogar Banachräume, so kann der Satz
vom abgeschlossenen Graphen oft zum Nachweis der Stetigkeit genutzt werden.
Allgemeiner kann man Stetigkeit auch für Abbildungen zwischen lokalkonvexen
Vektorräumen definieren und dann ist
genau dann stetig, wenn für jede stetige Halbnorm
auf
die Halbnorm
stetig auf
ist.
Stetigkeit von Grenzwerten von Funktionenfolgen
Im Allgemeinen folgt aus der punktweisen
Konvergenz einer Folge
stetiger Funktionen
nicht die Stetigkeit der Grenzfunktion
.
Zum Beispiel konvergiert für
die Funktionenfolge
gegen die unstetige Funktion
.
Unter strengeren Konvergenzbegriffen für Funktionenfolgen, insbesondere der (lokal) gleichmäßigen Konvergenz, kann aber stets die Stetigkeit der Grenzfunktion sichergestellt werden.
Mit Hilfe dieses Konvergenzbegriffs von Funktionenfolgen lässt sich die Stetigkeit von durch Potenzreihen definierten komplexen Funktionen im Innern ihres Konvergenzkreises beweisen (siehe auch Abelscher Grenzwertsatz).
Der Satz
von Banach-Steinhaus stellt die Stetigkeit der Grenzfunktion sicher, wenn
und
Banachräume sind und alle
lineare Operatoren sind.
Varianten des Stetigkeitsbegriffs
Für Funktionen zwischen metrischen Räumen gibt eine Reihe weiterer Stetigkeitsbegriffe, die jeweils strengere Bedingungen daran stellen, wie stark der Funktionswert in Abhängigkeit von der Schwankung im Argument schwanken darf. Hier wäre zu nennen: gleichmäßige Stetigkeit (kann auch für Funktionen auf uniformen Räumen definiert werden), (lokale) Lipschitz-Stetigkeit, Hölder-Stetigkeit, gleichgradige Stetigkeit sowie (falls der Definitionsbereich ein reelles Intervall ist) absolute Stetigkeit.
Stetigkeit in der Topologie
Das Konzept der Stetigkeit wurde zunächst für reelle und komplexe Funktionen entwickelt. Bei der Begründung des mathematischen Teilgebiets der Topologie zeigte sich aber, dass das Konzept sich natürlich auf dieses Gebiet erweitern lässt. Seitdem ist die Stetigkeit einer der Grundbegriffe der modernen Mathematik.
Die oben angegebenen alternativen Definitionen von Stetigkeit können leicht auf viel allgemeinere Situationen ausgedehnt werden, wobei ein Großteil der angegebenen Eigenschaften stetiger Funktionen ebenfalls verallgemeinert werden kann. Dieser verallgemeinerte Stetigkeitsbegriff ist von zentraler Bedeutung für die Topologie und verwandte mathematische Teilgebiete (etwa die Funktionalanalysis).
Definitionen der Stetigkeit
Da man topologische Räume auf unterschiedliche (aber äquivalente) Weise definieren kann, existieren auch mehrere gleichwertige Definitionen der Stetigkeit. Im Folgenden finden sich bei jeder Definition mehrere Varianten, die sich durch ihren Grad an Formalisierung unterscheiden, inhaltlich aber dasselbe aussagen.
Funktionen besitzen einen Definitionsbereich und eine Zielmenge, die mit verschiedenen Topologien versehen werden können. Die Wahl dieser Topologien ist kein Bestandteil der 'Identität' der Funktion aber wesentlich für die Frage der Stetigkeit. Es ist daher eigentlich unpräzise, davon zu sprechen, dass eine Funktion stetig oder unstetig sei.
Eine präzise Formulierung von der unten angegebenen Definition mittels Umgebungen würde zum Beispiel lauten:
Seien
und
topologische Räume. Sei
eine Funktion und
.
Dann heißt
stetig in
bezüglich der Räume
und
,
wenn für jede
-Umgebung
von
das Urbild
eine
-Umgebung
von
ist.
In der mathematischen Praxis ist fast immer klar, welche Topologien auf den jeweiligen Räumen verwendet werden sollen. Daher ist die in diesem Artikel verwendete etwas ungenaue Sprechweise üblich. In den seltenen Fällen, wo mehrere Topologien zur Auswahl stehen, wird dies durch entsprechende Erläuterungen deutlich gemacht.
Offene Mengen
- Eine Funktion zwischen zwei topologischen Räumen ist genau dann stetig, wenn die Urbilder offener Mengen wiederum offene Mengen sind.
- Sei
eine Abbildung von dem topologischen Raum
in den topologischen Raum
. Dann heißt
stetig, wenn das Urbild unter
von jeder in
offenen Menge
wieder offen in
ist.
stetig
(wobei
die Topologie des Raumes
, also die Menge der offenen Mengen des topologischen Raumes ist)
Abgeschlossene Mengen
Die Stetigkeit kann durch abgeschlossene Mengen definiert werden, indem man „offene Mengen“ in obiger Definition durch „abgeschlossene Mengen“ ersetzt:
- Eine Funktion zwischen zwei topologischen Räumen ist genau dann stetig, wenn die Urbilder abgeschlossener Mengen wiederum abgeschlossene Mengen sind.
- Sei
eine Abbildung von dem topologischen Raum
in den topologischen Raum
. Dann heißt
stetig, wenn das Urbild unter
von jeder in
abgeschlossenen Menge
wieder abgeschlossen in
ist.
stetig
Umgebungen
Sei
die Menge aller Umgebungen eines Punktes
.
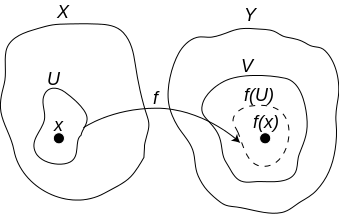
- Eine Funktion zwischen zwei topologischen Räumen ist genau dann stetig, wenn für jeden Punkt gilt: für jede Umgebung des Bildpunktes dieses Punktes gibt es eine Umgebung des Punktes, deren Bild komplett in der Umgebung des Bildpunktes liegt.
- Sei
eine Abbildung von dem topologischen Raum
in den topologischen Raum
. Dann ist
genau dann stetig, wenn für jeden Punkt
in
gilt: Ist
eine Umgebung von
, dann gibt es eine Umgebung
von
, so dass
in
enthalten ist.
stetig
Netze
Für eine gerichtete
Menge
und eine Menge
ist ein Netz
eine Abbildung
.
Meist schreibt man analog zu Folgen
.
Da die natürlichen
Zahlen mit der gewöhnlichen Anordnung eine gerichtete Menge bilden, sind
Folgen spezielle Netze.
- Seien
und
topologische Räume. Eine Abbildung
ist genau dann stetig, wenn für alle
gilt: Für jedes in
gegen
konvergierende Netz
konvergiert das Netz
in
gegen
stetig
Funktionen, die die schwächere Bedingung „“
erfüllen, werden folgenstetig in
genannt. Erfüllt
das erste Abzählbarkeitsaxiom
(dies ist z.B. für metrische Räume der Fall), so sind die beiden Begriffe
gleichwertig.
Abschluss
- Eine Funktion zwischen zwei topologischen Räumen ist genau dann stetig, wenn das Bild des Abschlusses einer beliebigen Teilmenge im Abschluss des Bildes dieser Teilmenge enthalten ist.
- Sei
eine Abbildung von dem topologischen Raum
in den topologischen Raum
. Dann ist
genau dann stetig, wenn für jede Teilmenge
von
gilt: Das Bild des Abschlusses von
liegt im Abschluss des Bildes von
.
stetig
Betrachtet man bei einer Funktion nicht wie bei der Stetigkeit die Urbilder, sondern die Bilder der Funktion, so gelangt man zu den Begriffen der offenen bzw. abgeschlossenen Abbildung.
Eigenschaften stetiger Funktionen
- Wenn
und
stetige Funktionen sind, dann ist die Komposition
auch stetig.
- Einschränkungen stetiger Funktionen sind stetig.
- Wenn
stetig und
- X kompakt
ist, dann ist
kompakt.
- X zusammenhängend
ist, dann ist
zusammenhängend.
- X wegzusammenhängend
ist, dann ist
wegzusammenhängend.
- X kompakt
ist, dann ist
- Stetigkeit ist eine lokale Eigenschaft.
Viele wichtige Sätze über Funktionen setzen voraus, dass diese stetig sind. Hier einige Beispiele:
- Der Satz von Peano über die Existenz von Lösungen gewöhnlicher Differentialgleichungen setzt die Stetigkeit der rechten Seite voraus.
- Der in der Topologie wichtige brouwersche Abbildungsgrad und seine in der Funktionalanalysis verwendeten Verallgemeinerungen sind für stetige Abbildungen definiert.
- Eine stetige Funktion von einer nichtleeren kompakten und konvexen Teilmenge eines hausdorffschen topologischen Vektorraums in sich selbst besitzt einen Fixpunkt (Fixpunktsatz von Schauder).
Beispiele stetiger Funktionen
Elementare Beispiele
- Für eine Definitionsmenge
mit der diskreten Topologie ist jede Funktion
in einen beliebigen Raum
stetig.
- Für eine Zielmenge
mit der indiskreten Topologie ist jede Funktion
in diesen Raum
stetig.
- Konstante Abbildungen zwischen beliebigen topologischen Räumen sind immer stetig.
- Für eine Definitionsmenge mit der indiskreten Topologie und eine Zielmenge, die ein T0-Raum ist, sind die konstanten Funktionen die einzigen stetigen Funktionen.
- Die identische
Abbildung
ist genau dann stetig, wenn die Topologie des Urbildraumes feiner ist, als die des Bildraumes, d.h.
.
Wege
Ist
ein topologischer Raum, so bezeichnet man eine stetige Funktion von
nach
auch als Weg
in
.
Dieser Begriff ist selbst wieder in verschiedenen Teilgebieten der Mathematik
von großer Bedeutung:
- Definition des Kurvenintegrals
- Definition des Wegzusammenhangs
- Definition der Fundamentalgruppe
Überraschend mag das Ergebnis sein, dass der n-dimensionale Einheitswürfel
für jedes
durch einen Weg vollständig ausgefüllt werden kann (Peano-Kurve).
Homöomorphismen
In der Algebra gilt, dass die Umkehrfunktion eines bijektiven Homomorphismus
wieder ein Homomorphismus ist. Homomorphismen sind per Definition dadurch
charakterisiert, dass ihre Anwendung mit der Ausführung der Rechenoperationen
vertauscht werden kann. Beim Beweis der Homomorphismus-Eigenschaft der
Umkehrfunktion nutzt man aus, dass die Rechenoperationen immer ausgeführt werden
können (im Definitionsbereich) und immer ein eindeutiges Ergebnis haben (in der
Zielmenge). Eine stetige Funktion kann charakterisiert werden als eine Funktion,
deren Anwendung mit der Grenzwertbildung (von Netzen) vertauscht werden kann. Da
aber Netze im Definitionsbereich nicht konvergieren müssen und in der Zielmenge
Netze auch gegen mehrere Grenzwerte konvergieren können, gilt eine analoge
Aussage über Umkehrfunktionen hier nicht. Dies zeigt zum Beispiel die bijektive
stetige Funktion .
Man bezeichnet eine bijektive Funktion zwischen zwei topologischen Räumen als Homöomorphismus,
wenn eine (und damit alle) der folgenden äquivalenten Bedingungen erfüllt ist:
(a) Die Funktion und ihre Umkehrfunktion sind stetig.
(b) Die Funktion und
ihre Umkehrfunktion sind offen.
(c) Die Funktion und ihre Umkehrfunktion sind
abgeschlossen.
(d) Die Funktion ist stetig und offen.
(e) Die Funktion ist
stetig und abgeschlossen.
Jede stetige Bijektion zwischen kompakten Hausdorff-Räumen ist ein Homöomorphismus.
Funktionen mehrerer Variablen
Eine Funktion, deren Definitionsbereich ein Kartesisches Produkt ist, wird auch als Funktion in mehreren Variablen bezeichnet. Die folgenden Ausführungen für den Fall eines Produktes von zwei topologischen Räumen können auf beliebige (auch unendliche) Produkte erweitert werden.
Seien ,
und
topologische Räume und
eine Funktion in zwei Variablen.
heißt stetig im ersten Argument, wenn für jedes
die Funktion
stetig ist. Analog wird die Stetigkeit im zweiten Argument definiert.
Ist die Funktion
stetig (hierbei wird auf
die Produkttopologie
angenommen), so ist
auch stetig in beiden Argumenten. Die Umkehrung gilt nicht, wie das Beispiel in
Stetige
Funktionen in mehreren Veränderlichen zeigt.
Die umgekehrte Situation ist deutlich einfacher: Für eine Funktion
gibt es (eindeutig bestimmte) Funktionen
und
,
so dass
für alle
.
Dann ist
genau dann stetig, wenn
und
es sind. Man kann also
in natürlicher Weise mit
identifizieren.
Menge der stetigen Funktionen
Die Menge aller stetigen Funktionen von
nach
wird meist mit
oder
bezeichnet. Dabei steht das C für „continuous“, englisch für „stetig“. Ist der
Bildraum
aus dem Kontext ersichtlich oder
,
so schreibt man oft nur
bzw.
.
ist eine Unteralgebra
der
-Algebra
aller reellwertigen Funktionen auf
.
Zwei stetige Funktionen von
nach
stimmen bereits überein, wenn sie auf einer dichten
Teilmenge von
übereinstimmen. Da jede Teilmenge von
eine höchstens
abzählbare dichte Teilmenge besitzt, kann man hieraus ableiten, dass die Mächtigkeit
von
die Mächtigkeit
des Kontinuums ist (falls
nicht leer ist). Die Menge aller Funktionen von
nach
hat eine wesentlich größere Mächtigkeit (zumindest, wenn
ein Intervall mit mehr als einem Element ist). Man kann das so interpretieren,
dass Stetigkeit unter reellen Funktionen eine 'seltene' Eigenschaft ist. Dies
widerspricht etwas der Alltagserfahrung, da ja alle elementaren Funktionen
stetig sind.
Wichtige Unterräume von
sind zum Beispiel:
- falls
eine differenzierbare Mannigfaltigkeit ist: die Menge der stetig differenzierbaren Funktionen
und
- die Menge der beliebig
oft differenzierbaren Funktionen
.
Ist
ein kompakter
Raum, so tragen die stetigen Funktionen mehr Struktur. Ist dann zusätzlich
ein metrischer
Raum, zum Beispiel wieder
,
so sind die stetigen Funktionen stets eine Teilmenge der beschränkten
Funktionen, es gilt also
.
Ist auf
eine Norm
definiert, so wird über
eine Norm auf
definiert, die sogenannte Supremumsnorm.
Diese Definition ist aufgrund der Beschränktheit stetiger Funktionen auf
kompakten Räumen sinnvoll.
Ist
ein Banach-Raum,
also ein vollständiger
normierter Raum, so ist auch
ein Banach-Raum. Die stetigen Funktionen sind dann ein abgeschlossener
Unterraum der beschränkten Funktionen.
Zu einer Familie stetiger Funktionen kann man auf dem Definitionsbereich nach einer möglichst groben Topologie sucht, bezüglich der die Funktionen immer noch stetig sind, bzw. auf der Zielmenge nach einer möglichst feinen. Diese Topologien werden als Initialtopologie und Finaltopologie bezeichnet.
Algebren stetiger komplexwertiger Funktionen
Für einen topologischen Raum
bildet
,
die Menge der stetigen komplexwertigen Funktionen auf
,
wie bereits festgestellt, eine
-Algebra.
Diese ist natürlich kommutativ
und unital
(die Funktion mit dem konstanten Wert 1 ist das Einselement).
Zusätzlich ist auf dieser Algebra in natürlicher Weise eine konjugiert
lineare Involution
gegeben, die auch mit der Multiplikation verträglich ist. Diese ist gegeben
durch
für
.
ist also eine unitale,
kommutative
*-Algebra.
Man beachte, dass die Untersuchung dieser Algebren die Untersuchung der
Algebren aller komplexwertigen Funktionen auf einer beliebigen Menge
einschließt, da man jede Menge mit der diskreten Topologie versehen kann,
wodurch alle Funktionen stetig werden.
Das Lemma
von Urysohn stellt für die meisten wichtigen topologischen Räume sicher,
dass
ausreichend reichhaltig ist. Tatsächlich erweist sich diese Algebra als oftmals
zu groß für die praktische Untersuchung. Man geht daher meist zur unitalen
*-Unteralgebra
der beschränkten, stetigen komplexwertigen Funktionen auf
über. Falls
kompakt ist, so gilt
,
wegen (15').
wird durch die Supremumsnorm
zu einer kommutativen, unitalen C*-Algebra.
Der Satz
von Gelfand-Neumark besagt, dass jede kommutative, unitale C*-Algebra
isomorph ist zu
für einen geeignet gewählten kompakten Hausdorff-Raum
.
Dabei ist
bis auf Homöomorphie eindeutig bestimmt (und der Satz gibt auch ein
konstruktives Verfahren zur Ermittlung von
an). Somit kann die Theorie der kommutativen, unitalen C*-Algebren vollständig
identifiziert werden mit der Theorie der kompakten Hausdorff-Räume. Dies ist ein
mächtiges Werkzeug, da Aussagen, die in der einen Theorie schwierig zu beweisen
sind, in die andere Theorie übertragen werden können, wo ihr Beweis oft viel
einfacher ist.
In Erweiterung dieses Ergebnisses kann die Theorie der kommutativen,
eventuell nicht unitalen, C*-Algebren mit der Theorie der lokalkompakten
Hausdorff-Räume identifiziert werden. Hierbei wird allerdings zu einem
lokalkompakten Hausdorff-Raum
nicht
,
sondern die Unteralgebra der C0-Funktionen
auf
betrachtet.
Bemerkung: Mittels der GNS-Konstruktion kann auch jede nicht-kommutative C*-Algebra mit einer Algebra stetiger (linearer) Funktionen identifiziert werden. Hierbei wird allerdings als Multiplikation die Komposition von Operatoren und nicht die punktweise Multiplikation verwendet. Daher sollten diese beiden Vorgehensweisen nicht miteinander verwechselt werden.
Zwei weitere wichtige Ergebnisse über die Struktur von
für kompakte Hausdorff-Räume
sind der Satz
von Stone-Weierstraß (Charakterisierung der dichten *-Unteralgebren von
)
und der Satz
von Arzelà-Ascoli (Charakterisierung der relativ
kompakten Teilmengen von
).
Ein Spezialfall des ersten Satzes ist der
Approximationssatz von Weierstraß,
der besagt, dass auf einer kompakten Teilmenge von
jede stetige, komplexwertige Funktion gleichmäßig
durch eine Folge von Polynomfunktionen approximiert werden kann.
Verknüpfung von algebraischen und topologischen Strukturen
Viele der in der Mathematik untersuchten Mengen tragen in natürlicher Weise
sowohl eine topologische als auch eine algebraische Struktur. Ein einfaches
Beispiel hierfür sind die Mengen
und
,
die durch die Betragsmetrik zu metrischen Räumen werden, und die gleichzeitig
durch die Grundrechenarten zu Körpern
werden. Eine besonders reichhaltige Theorie ergibt sich, wenn diese beiden
Strukturen harmonieren. Dies ist dann gegeben, wenn die Verknüpfung(en),
die die algebraische Struktur definieren, stetige Funktionen bezüglich der
betrachteten Topologie sind. Auf diese Weise ergeben sich sehr einfach die
Definition einer topologischen
Gruppe, eines topologischen
Rings/Körpers und eines topologischen
Vektorraums.
Hat man zwei Exemplare einer solchen Kategorie (also etwa zwei topologische Gruppen), so bietet es sich an, die Funktionen zwischen diesen beiden zu untersuchen, die verträglich mit beiden Strukturen sind, die also stetige Homomorphismen sind. In der Funktionalanalysis werden zum Beispiel intensiv die Eigenschaften von (Räumen von) stetigen linearen Operatoren untersucht. In allen genannten Kategorien ist ein Homomorphismus übrigens entweder stetig oder in jedem Punkt unstetig.
Mit dem Auswahlaxiom
kann man zahlreiche unstetige Homomorphismen zwischen topologischen Gruppen
konstruieren, insbesondere auch zahlreiche unstetige Homomorphismen .
Andererseits sind stetige Homomorphismen zwischen Lie-Gruppen stets differenzierbar.
Geschichte
Augustin-Louis Cauchy und Bernard Bolzano gaben Anfang des 19. Jahrhunderts unabhängig voneinander eine Definition der Stetigkeit. Ihr Stetigkeitsbegriff unterschied sich grundsätzlich von dem Eulerschen, wonach eine Funktion stetig heißt, falls sie durch einen einzigen analytischen Ausdruck beschrieben werden kann. Unter einem analytischen Ausdruck verstand Euler Ausdrücke, die durch endliche (algebraische Funktionen) oder unendliche (transzendente Funktionen) Anwendung algebraischer Operationen wie Addition, Subtraktion, Multiplikation, Division, Wurzelziehen gebildet werden. Im Eulerschen Sinne galt die Betragsfunktion als unstetig, weil durch zwei analytische Ausdrücke gegeben, während nach der auf Cauchy und Bolzano zurückgehenden Definition diese Funktion stetig ist.
Cauchy und Bolzano nannten eine Funktion stetig, wenn hinreichend kleine
Änderungen des Arguments nur beliebig kleine Änderungen des Funktionswerts nach
sich zögen. Dies war bereits eine exakte Definition, die aber in ihrer
praktischen Anwendung gewisse Fragen offenlässt. Das heutzutage übliche -
-Kriterium
wurde von Karl
Weierstraß in seinem viersemestrigen Vorlesungszyklus verwendet, den er
zwischen 1857 und 1887 insgesamt sechzehnmal gehalten hat.
Lange Zeit war offen, ob es auch stetige reelle Funktionen gibt, die nirgends differenzierbar sind. Das erste Beispiel einer reellen stetigen aber nirgends differenzierbare Funktion wurde von Bernard Bolzano konstruiert (Bolzanofunktion). Dieses Beispiel wurde aber erst deutlich später veröffentlicht. Bekannt wurde die Existenz solcher Funktionen durch Karl Weierstraß (Weierstraß-Funktion), der damit viele zeitgenössische Mathematiker überraschte.
Siehe auch
- Oszillation einer Funktion
- Unstetigkeitsstelle
- Definitionslücke
- Hebbare Definitionslücke
- Links- und rechtsseitige Stetigkeit
- Polstelle
- Stetige Differenzierbarkeit und höhere Ableitungen
Literatur
- Harro Heuser: Lehrbuch der Analysis. Teubner, Wiesbaden 2003, ISBN 3-519-62233-5
- Boto von Querenburg: Mengentheoretische Topologie (= Springer-Lehrbuch). 3., neu bearbeitete und erweiterte Auflage. Springer-Verlag, Berlin [u.a.] 2001, ISBN 3-540-67790-9.
- Friedrich Hirzebruch / Winfried Scharlau: Einführung in die Funktionalanalysis (= Reihe „B. I.-Hochschultaschenbücher“, Band Nr. Band 296). Bibliographisches Institut, Mannheim [u.a.] 1971, ISBN 3-411-00296-4.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.11. 2021