Umkehrfunktion
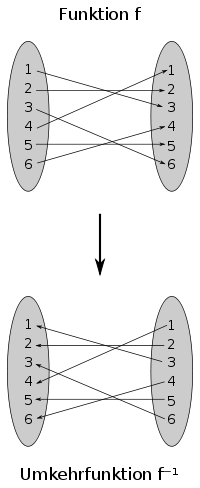
In der Mathematik bezeichnet die Umkehrfunktion oder inverse Funktion einer bijektiven Funktion die Funktion, die jedem Element der Zielmenge sein eindeutig bestimmtes Urbildelement zuweist.
Eine Funktion
ein eindeutig bestimmtes Element
zu, das mit
bezeichnet wird. Gilt für
die Beziehung
,
so sagt man auch, dass
ein Urbildelement von
unter
ist. Im Allgemeinen kann ein Element von
kein, ein oder mehrere Urbildelemenete unter
besitzen. Falls jedes Element von
genau ein Urbildelement unter
besitzt (man spricht dann von dem Urbildelement), nennt man
invertierbar. In diesem Fall kann man eine Funktion
definieren, die jedem Element von
ihr eindeutig definiertes Urbildelement unter
zuordnet. Diese Funktion wird dann als die Umkehrfunktion von
bezeichnet.
Man kann leicht nachweisen, dass eine Funktion genau dann invertierbar ist,
wenn sie bijektiv (also gleichzeitig injektiv und surjektiv)
ist. Tatsächlich besagt die Injektivität nichts anderes, als dass jedes Element
von
höchstens ein Urbildelement unter
besitzt. Die Surjektivität besagt gerade, dass jedes Element von
mindestens ein Urbildelement unter
besitzt.
Der Begriff der Umkehrfunktion gehört formal zum mathematischen Teilgebiet der Mengenlehre, wird aber in vielen Teilgebieten der Mathematik verwendet.
Definition
Seien
und
nicht-leere Mengen.
Neben der Definition aus der Einleitung gibt es weitere Möglichkeiten, die
Begriffe der Invertierbarkeit einer Funktion
und der Umkehrfunktion einer invertierbaren Funktion formal einzuführen:
- Man sucht nach einer Funktion
, so dass
für alle
und
für alle
. Es stellt sich heraus, dass es höchstens ein solches
geben kann. Existiert dies, so nennt man
invertierbar und das eindeutig bestimmte
die Umkehrfunktion von
.
- Unter Verwendung der Komposition
von Funktionen kann die vorherige Bedingung auch etwas eleganter formuliert
werden, indem man für
fordert:
und
. Dabei ist
die identische Abbildung auf der Menge
.
- Man führt zunächst die weiter unten erklärten Begriffe von Linksinversen und Rechtsinversen ein. Dann nennt man eine Funktion invertierbar, wenn sie sowohl eine Linksinverse als auch eine Rechtsinverse besitzt. Es zeigt sich, dass in diesem Fall Linksinverse und Rechtsinverse übereinstimmen müssen (womit auch folgt, dass es in diesem Fall davon nicht mehrere gibt). Diese eindeutig bestimmte Links- und Rechtsinverse ist dann die Umkehrfunktion.
- Man bezieht sich bei der Definition darauf, dass eine Funktion von
nach
immer auch eine Relation von
nach
ist. Daher besitzt sie auf jeden Fall eine Umkehrrelation. Man nennt
invertierbar, wenn diese Umkehrrelation eine Funktion von
nach
ist. In diesem Fall wird die Umkehrrelation auch als Umkehrfunktion bezeichnet.
Es stellt sich heraus, dass alle vorgestellten Invertierbarkeitsbegriffe äquivalent zum Begriff der Bijektivität sind. Auch führen alle Definitionen der Umkehrfunktion zum gleichen Ergebnis.
Notation
Wenn
eine bijektive Funktion ist, dann bezeichnet
die Umkehrfunktion. Dabei ist die hochgestellte
nicht mit einer negativen Potenz
bezüglich der Multiplikation
zu verwechseln. Es handelt sich vielmehr um die Umkehrung bezüglich der
Komposition von Funktionen. Die alternative Schreibweise
(f quer),
kann leicht mit der komplexen
Konjugation verwechselt werden. Sie wird daher in der mathematischen
Literatur nur selten verwendet.
Allerdings besteht auch bei der Notation
eine Doppeldeutigkeit. Diese Notation wird nämlich auch für die Urbildfunktion
verwendet, die für jede Funktion (also auch nicht bijektive) existiert. Die
Urbildfunktion ist eine Funktion von der Potenzmenge
in die Potenzmenge
.
Es ist üblich, in der Notation der Urbildfunktion bei einelementigen Mengen die
Mengenklammern wegzulassen. Für
wird also statt
auch einfach
geschrieben. Identifiziert man nun in dieser notationellen Weise die
einelementige Menge mit dem einen enthaltenen Element, dann ist die
Umkehrfunktion eine Spezialisierung der Urbildfunktion, und frontale
Widersprüche können nicht auftreten. Denn für bijektive
ist
das eine und einzige Element der Urbildmenge
.
Wegen der genannten Verwechslungsmöglichkeit findet sich gelegentlich in der
Literatur für die Umkehrfunktion (das ist die -te
Iteration) die Schreibweise
-
so dass /TD>
(mit hochgestellter spitzer Klammer),
für die Iteration
-
und ,
für die Potenz
-
und (ohne hochgestellte Klammer)
und für die Ableitung
-
und (mit hochgestellter runder Klammer).
Dann ist beispielsweise
und
Einfache Beispiele
- Sei
die Menge der 26 Buchstaben des lateinischen Alphabets und sei
. Die Funktion
, die jedem Buchstaben die entsprechende Nummer im Alphabet zuordnet, ist bijektiv, und
ist gegeben durch
„der n-te Buchstabe im Alphabet“.
- Sei
die reelle Funktion mit
. Diese ist bijektiv und die Umkehrfunktion ist gegeben durch
-
.
- Allgemeiner: Sind
und die Funktion
gegeben durch
. Dann ist
genau dann bijektiv, wenn
. In diesem Fall gilt
.
Eigenschaften
- Die Umkehrfunktion ist selber bijektiv. Ihre Umkehrfunktion ist die ursprüngliche Funktion, d.h.
-
.
- Ist
eine bijektive Funktion, dann gilt für die Umkehrfunktion:
-
für alle
,
für alle
.
- Oder etwas eleganter:
.
- Sind
und
zwei Funktionen mit der Eigenschaft
-
für alle
dann kann aus jeder der drei folgenden Eigenschaften bereits geschlossen werden, dass beide Funktionen bijektiv und ihre gegenseitigen Umkehrfunktionen sind:
-
für alle
,
ist injektiv
ist surjektiv
- Sind die Funktionen
und
bijektiv, dann gilt dies auch für die Komposition
. Die Umkehrfunktion von
ist dann
.
- Eine Funktion
kann ihre eigene Umkehrfunktion sein. Dies gilt genau dann, wenn
. In diesem Fall nennt man
eine Involution. Die einfachsten involutorischen Abbildungen sind die identischen Abbildungen.
- Ist
eine bijektive Funktion, wobei
und
Teilmengen von
sind, dann entsteht der Graph der Umkehrfunktion, indem man den Graph von
an der Geraden
spiegelt.
- Ist
differenzierbar,
und
, dann gilt die folgende Umkehrregel:
-
.
- Diese Aussage wird in der mehrdimensionalen Analysis zum Satz von der Umkehrabbildung verallgemeinert.
Umkehrfunktion für nicht bijektive Funktionen
In vielen Fällen besteht der Wunsch nach einer Umkehrfunktion für eine nicht bijektive Funktion. Hierzu kann man die folgenden Hilfsmittel heranziehen:
- Ist die Funktion nicht surjektiv, so kann man die Zielmenge verkleinern, indem man hierfür gerade das Bild der Funktion wählt. Die so erhaltene Funktion ist surjektiv und stimmt in ihrem Verlauf mit der ursprünglichen Funktion überein. Dieser Ansatz ist immer möglich. Es kann allerdings sein, dass es schwierig ist, das Bild der betrachteten Funktion genau zu bestimmen. Außerdem kann beim Übergang auf diese Teilmenge eine wichtige Eigenschaft der ursprünglich betrachteten Zielmenge verloren gehen (in der Analysis etwa die Vollständigkeit).
- In manchen Fällen erweist es sich auch als fruchtbar, die gewünschte Surjektivität dadurch zu erreichen, dass man bei der betrachteten Funktion den Definitionsbereich erweitert. Oft geht das auch mit einer Erweiterung der Zielmenge einher. Ob dieser Weg gangbar und sinnvoll ist, muss aber jeweils individuell entschieden werden.
- Ist die Funktion nicht injektiv, so kann man auf ihrem Definitionsbereich eine geeignete Äquivalenzrelation definieren, so dass man die Funktion auf die Menge der entsprechenden Äquivalenzklassen übertragen kann. Diese Funktion ist dann automatisch injektiv. Dieser Ansatz ist allerdings anspruchsvoll und führt zu einem oft unerwünschten Wechsel in der Natur der Argumente der betrachteten Funktion.
- In der Praxis kann man die Injektivität der Funktion oft auch dadurch erreichen, dass man sich auf eine geeignete Teilmenge des Definitionsbereichs der Funktion einschränkt, die zu jedem Element des Bilds nur ein einziges Urbildelement enthält. Diese Einschränkung ist allerdings unter Umständen willkürlich. Man muss daher darauf achten, dass man diese Einschränkung an allen Stellen konsistent in gleicher Weise vornimmt.
Beispiele
- Man betrachte die Nachfolger-Funktion
auf der Menge
der natürlichen Zahlen ohne die Null. Diese Funktion ist injektiv. Sie ist aber nicht surjektiv, da die Zahl 1 nicht als Funktionswert vorkommt. Man kann nun die Zahl 1 aus der Zielmenge entfernen. Dann wird die Funktion surjektiv und die Vorgänger-Funktion
ist ihre Umkehrfunktion. Allerdings ist es unschön, dass bei der Funktion nun Definitionsbereich und Zielmenge nicht mehr übereinstimmen.
- Die alternative Idee, den Definitionsbereich um das fehlende Urbildelement
für die 1, nämlich die 0, zu erweitern, hat auf den ersten Blick denselben
Nachteil. Fügt man, um dies zu beheben, die 0 ebenfalls zur Zielmenge hinzu,
so besitzt diese wiederum kein Urbildelement. Man kann diesen Prozess aber
gedanklich unendlich oft fortsetzen und gelangt dadurch zur Menge
der ganzen Zahlen. Auf dieser Menge ist die Nachfolger-Funktion bijektiv, und ihre Umkehrfunktion ist die Vorgänger-Funktion.
- Die Exponentialfunktion
betrachtet als Funktion von
nach
ist injektiv aber nicht surjektiv. Ihr Bild ist gerade die Menge der positiven reellen Zahlen. Schränkt man die Zielmenge darauf ein, so erhält man eine bijektive Funktion, deren Umkehrfunktion die Logarithmusfunktion ist. Eine natürliche Erweiterung des Zahlbereichs, wie im vorherigen Beispiel diskutiert, bietet sich hier nicht an. Daher muss man akzeptieren, dass bei den betrachteten Funktionen nun Definitionsbereich und Zielmenge nicht mehr übereinstimmen.
- Die Quadratfunktion
ist betrachtet als Funktion von
nach
weder injektiv noch surjektiv. Die Surjektivität erreicht man dadurch, dass man als Zielmenge die Bildmenge
der nichtnegativen reellen Zahlen wählt. Um die Injektivität zu erreichen, kann man den Definitionsbereich einschränken. Am naheliegendsten ist es, hier ebenfalls
zu wählen. Die so erhaltene eingeschränkte Quadratfunktion ist bijektiv. Ihre Umkehrfunktion ist die Quadratwurzelfunktion.
- Die trigonometrischen Funktionen Sinus (sin), Kosinus (cos) und Tangens (tan) sind nicht bijektiv. Man schränkt sich jeweils auf geeignete Teilmengen des Definitionsbereichs und der Zielmenge ein und erhält bijektive Funktionen, deren Umkehrfunktionen die Arkusfunktionen: Arkussinus (arcsin), Arkuskosinus (arccos) und Arkustangens (arctan) sind.
- Ein entsprechendes Vorgehen für die Hyperbelfunktionen Sinus hyperbolicus (sinh), Cosinus hyperbolicus (cosh) und Tangens hyperbolicus (tanh) führt zu den Areafunktionen: Areasinus hyperbolicus (arsinh), Areakosinus hyperbolicus (arcosh) und Areatangens hyperbolicus (artanh).
Berechnung
Die effektive Bestimmung der Umkehrfunktion ist oft schwierig. Asymmetrische Verschlüsselungsverfahren beruhen darauf, dass die Bestimmung der Umkehrfunktion einer Verschlüsselungsfunktion effektiv nur möglich ist, wenn man einen geheimen Schlüssel kennt. Dabei ist die Berechnungsvorschrift für die Verschlüsselungsfunktion selbst öffentlich bekannt.
Reelle Funktionen sind oft durch eine Berechnungsvorschrift definiert, die
durch einen arithmentischen Term
(mit einer Variablen
)
beschrieben werden kann. Bei der Suche nach der Umkehrfunktion versucht man nun
die Funktionsgleichung
durch Äquivalenzumformung
in die Form
(für einen passenden Term
)
zu bringen, also äquivalent nach
aufzulösen. Gelingt dies, so ist die durch die Berechnungsvorschrift
definierte Funktion als bijektiv erwiesen und
ist eine Berechnungsvorschrift für die Umkehrfunktion. Man beachte, dass bei den
Schritten der Äquivalenzumformung die Mengen, aus denen
und
gewählt werden sollen, genau zu beachten sind. Sie bilden dann
Definitionsbereich und Zielmenge der betrachteten Funktion.
Beispiele:
- Sei
mit
. Die folgenden Gleichungen sind äquivalent:
- Die Umkehrfunktion von
lautet daher
. Da es üblich ist, das Argument mit
zu bezeichnen, schreibt man auch:
.
- Sei
mit
. Die folgenden Gleichungen sind äquivalent (man beachte, dass
gilt):
- (Die zweite Lösung der quadratischen
Gleichung entfällt, da
als positiv vorausgesetzt ist.) Die Umkehrfunktion lautet also:
- Bemerkung: Bei dieser Lösung wurde die Quadratwurzel verwendet. Die
Quadratwurzelfunktion ist gerade definiert als die Umkehrfunktion der
einfachen Quadratfunktion
. Diese einfache Funktion kann nämlich nicht unter Verwendung der Grundrechenarten 'umgekehrt' werden.
- Dieses Problem wurde dadurch gelöst, dass der Vorrat an mathematischen Standardoperationen um ein weiteres Mitglied (nämlich die Quadratwurzel) erweitert wurde.
- Die Leistung der oben durchgeführten Umformung besteht also darin, die
Berechnung für die Umkehrfunktion der Funktion
auf die Berechnung der Umkehrfunktion der Quadratfunktion zurückgeführt zu haben.
- Die Quadratwurzel kann, wie gesagt, nicht auf elementare Weise berechnet werden. Tatsächlich hat sie selbst für ganzzahlige Argumente oft irrationale Werte. Es gibt aber gut verstandene Näherungsverfahren für die Quadratwurzel.
- Daher wird obige Umformung als ausreichend angesehen. Tatsächlich lässt sich ein besseres Ergebnis auch nicht erzielen.
- Man beachte, dass auch die anderen oben angegebenen Umkehrfunktionen (Logarithmus, Arcus- und Area-Funktionen) nicht mit Hilfe der Grundrechenarten (und der Exponentialfunktion und den trigonometrischen Funktionen) berechnet werden können. Sie erweitern daher, genau wie die Quadratwurzel, die Menge der mathematischen Standardoperationen (siehe auch Elementare Funktion).
Umkehrfunktionen und Morphismen
In der höheren Mathematik werden oft Mengen betrachtet, die noch mit zusätzlicher mathematischer Struktur versehen sind. Ein einfaches Beispiel hierfür ist die Menge der natürlichen Zahlen, auf der es unter anderem die durch die Kleiner-Relation definierte Ordnungsstruktur gibt.
Betrachtet man nun Funktionen zwischen zwei Mengen, die den gleichen Typ von Struktur tragen (also etwa zwei geordnete Mengen), so interessiert man sich besonders für Funktionen zwischen diesen Mengen, die mit den entsprechenden Strukturen 'verträglich' sind. Diese Verträglichkeit muss dabei gesondert definiert werden. Die Definition ist aber in den meisten Fällen naheliegend.
Funktionen, die diese Verträglichkeit erfüllen, werden auch Morphismen genannt. Bei geordneten Mengen sind die Morphismen etwa die monotonen Funktionen.
Ist ein Morphismus bijektiv, so stellt sich die Frage, ob die Umkehrfunktion ebenfalls ein Morphismus ist.
In vielen Teilgebieten der Mathematik ist dies automatisch der Fall. So sind etwa die Umkehrfunktionen bijektiver Homomorphismen automatisch ebenfalls Homomorphismen.
In anderen Teilgebieten ist dies nicht der Fall. Bei den geordneten Mengen kommt es zum Beispiel darauf an, ob man sich auf Totalordnungen beschränkt (dann sind Umkehrfunktionen von monotonen Funktionen wieder monoton) oder ob man auch Halbordnungen zulässt (dann ist dies nicht immer der Fall).
Ein bijektiver Morphismus, dessen Umkehrfunktion ebenfalls ein Morphismus ist, wird auch Isomorphismus genannt.
Umkehrfunktionen von Linearen Abbildungen
Ein besonders wichtiges Beispiel für den Morphismusbegriff ist der Begriff der linearen Abbildung (dem Vektorraumhomomorphismus). Eine bijektive linearen Abbildung ist immer ein Isomorphismus. Oft stellt sich die Frage, wie deren Umkehrfunktion effektiv bestimmt werden kann.
Damit überhaupt ein solcher Isomorphismus existieren kann, müssen die beiden beteiligten Vektorräume dieselbe Dimension haben. Ist diese endlich, so lässt sich jede lineare Abbildung zwischen den Räumen durch eine quadratische Matrix (mit entsprechender Spaltenzahl) darstellen. Die lineare Abbildung ist dann genau dann bijektiv, wenn diese Matrix eine Inverse besitzt. Diese Inverse beschreibt dann die Umkehrfunktion.
Im mathematischen Teilgebiet der Funktionalanalysis betrachtet man vor allem unendlichdimensionale Vektorräume, die neben der Vektorraumstruktur noch eine zusätzliche topologische Struktur tragen. Als Morphismen lässt man hier nur solche linearen Abbildungen gelten, die auch mit den topologischen Strukturen verträglich, das heißt stetig, sind. Im Allgemeinen ist die Umkehrfunktion einer bijektiven stetigen linearen Abbildung zwischen zwei topologischen Vektorräumen nicht zwangsläufig stetig. Sind aber beide beteiligten Räume Banachräume, so folgt aus dem Satz über die offene Abbildung, dass dies der Fall sein muss.
Verallgemeinerungen
Für allgemeinere Anwendungen ist der oben eingeführte Begriff der Umkehrfunktion als Inverses einer Bijektion zu eng. Entsprechend existieren Verallgemeinerungen für solche Gegebenheiten, von denen zwei nachfolgend vorgestellt werden.
Linksinverse
Für eine Funktion
heißt eine Funktion
Linksinverse
(oder Retraktion),
wenn
Das heißt, die Funktion
erfüllt
Das Verhalten von
auf dem Bild von
ist also festgelegt. Für Elemente aus
,
die nicht Resultat von
sind, kann
dagegen beliebige Werte annehmen. Eine Funktion
hat Linksinverse genau dann, wenn sie injektiv (linkseindeutig) ist.
Eine injektive Funktion kann mehrere Linksinverse haben. Dies ist genau dann der Fall, wenn die Funktion nicht surjektiv ist und der Definitionsbereich mehr als ein Element besitzt.
- Beispiele
Linksinverse treten oft als 'Inverse' von Einbettungen auf.
Sei zum Beispiel
die Menge der Vereine, die in der Saison
2018/19 mit einer Mannschaft in der ersten Fußball-Bundesliga der Männer
vertreten sind.
sei die Menge der Kommunen in Deutschland. Die Funktion
ordne einem Verein die Kommune zu, in der sein Stadion steht. Da in der
betrachteten Saison keine zwei Bundesliga-Mannschaften aus derselben Stadt
kommen, ist diese Funktion injektiv. Da es auch Kommunen ohne Bundesliga-Stadion
gibt, ist sie nicht surjektiv. Es gibt also mehrere Linksinverse zu
.
Eine einfach zu bildende Linksinverse ist die Funktion, die jeder Kommune, die
ein Bundesliga-Stadion besitzt, den zugehörigen Verein und allen anderen
Kommunen den FC
Bayern München zuordnet. Ein in der Praxis sinnvolleres Beispiel wäre die
Funktion, die jeder Kommune den Bundesliga-Verein mit dem am nächsten gelegenen
Stadion zuordnet. Allerdings wäre es auch deutlich aufwändiger diese Funktion zu
ermitteln, zumal erst einmal geklärt werden müsste, welcher Abstandsbegriff der
Definition zu Grunde liegt (Luftlinie, kürzeste Entfernung mit dem PKW, …).
Als numerisches Beispiel sei
die Einbettung von
in
.
Dann bietet sich jede Rundungsfunktion
(auf 0 Stellen nach dem Komma), also zum Beispiel die Gaußklammer, als
Linksinverse an. Aber auch die Funktion auf
,
die jeder ganzen Zahl sich selbst und allen anderen Zahlen die 0 zuordnet, ist
eine Linksinverse.
Rechtsinverse
Eine Rechtsinverse (Koretraktion) von
(oder, bei Faserbündeln,
ein Schnitt
von
)
ist eine Funktion
,
so dass
Das heißt, die Funktion
erfüllt
kann also jedes Urbildelement von
unter
sein.
Hat eine Funktion
eine Rechtsinverse, so muss sie surjektiv (rechtstotal) sein.
Umgekehrt scheint es offensichtlich, dass aus der Surjektivität von
die Existenz einer Rechtsinversen folgt. Zu jedem
kann man ja ein oder sogar mehrere Urbildelemente unter
in
finden. Ist die Funktion allerdings 'hochgradig nicht-injektiv', so muss hierzu
für eine unüberschaubare Menge von Elementen der Zielmenge eine Entscheidung
getroffen werden, welches der Urbildelemente man denn jeweils wirklich nimmt.
Eine solche simultane Entscheidung kann nicht immer konstruktiv getroffen
werden. Das Auswahlaxiom
(in geeigneter Formulierung) besagt gerade, dass eine Rechtsinverse trotzdem für
alle surjektiven Funktionen existiert.
In vielen Fällen kann allerdings die Auflösung der Uneindeutigkeit durch eine globale Festlegung erfolgen. Dies ist etwa bei der Definition der Quadratwurzel der Fall, wo man die Uneindeutigkeit immer zu Gunsten der positiven Lösung auflöst. In solchen Fällen wird das Auswahlaxiom nicht benötigt.
Die Funktion
ist offenbar genau dann Rechtsinverse von
,
wenn
Linksinverse von
ist. Hieraus folgt unmittelbar, dass Rechtsinverse immer injektiv und
Linksinverse immer surjektiv sind.
Eine surjektive Funktion hat genau dann mehrere Rechtsinverse, wenn sie nicht injektiv ist.
- Beispiele
Rechtsinverse treten oft als Funktionen auf, die Repräsentanten einer Menge bestimmen.
Sei beispielsweise
eine Funktion, die jeder Art
ihre Gattung
zuweist. Als Rechtsinverse
wählt man dann eine Funktion, die für jede Gattung eine typische Art benennt.
Politische Vertretung liefert viele Beispiele. Hier könnte
etwa die Staatsangehörigkeit eines Menschen sein,
das Staatsoberhaupt eines Staates.
Die Hilbert-Kurve bildet das Einheitsintervall stetig (daher die Bezeichnung Kurve) auf das Einheitsquadrat ab. In der praktischen Anwendung wird aber häufig der Hilbert-Index benötigt, nämlich eine Linearisierung zweidimensionaler Daten (eine Umkehrung der Hilbert-Kurve). Dazu nimmt man eine der Rechtsinversen der Hilbert-Kurve, von denen es mehrere gibt – denn die Hilbert-Kurve kann als stetige Abbildung zwischen zwei Räumen unterschiedlicher Dimension nach dem Satz von der Invarianz der Dimension nicht bijektiv sein.
Links- und Rechtsinverse von Morphismen
Tragen die Mengen
und
eine zusätzliche mathematische Struktur und ist
eine injektive bzw. surjektive Funktion, die mit diesen Strukturen verträglich
ist, so stellt sich die Frage, ob es möglich ist, die Links- bzw. Rechtsinverse
so zu wählen, dass die ebenfalls mit den Strukturen verträglich ist. Für viele
in der Mathematik untersuchte Strukturen ist dies nicht der Fall. Ist
allerdings eine injektive bzw. surjektive lineare Abbildung, so kann man die
Links- bzw. Rechtsinverse ebenfalls als lineare Abbildung wählen.
Verschiedenes
- Von besonderem Interesse sind oft Funktionen, bei den Definitionsbereich
und Zielmenge übereinstimmen. Für eine Menge
bildet die Menge der Funktionen von
in sich mit der Komposition als Verknüpfung einen Monoid. Die Begriffe der Invertierbarkeit sowie des Links- und Rechtsinversen, die hier eingeführt wurden, stimmen dann mit den entsprechenden Begriffen aus der Algebra überein.
- Der Begriff der Umkehrfunktion ist in diesem Fall identisch mit dem Begriff des inversen Elements.
- Im allgemeinen Kontext wird der Begriff der Invertierbarkeit von Funktionen oft weggelassen, da er mit dem Begriff der Bijektivität übereinstimmt.
- Bei den obigen Überlegungen wurde vorausgesetzt, dass
und
nicht-leer sind. Ist
leer, so gibt es überhaupt nur dann eine Funktion von
nach
, wenn
ebenfalls leer ist.
- Diese ist dann die leere Funktion, die bijektiv und involutorisch ist.
- Ist
, aber nicht
, leer, so gibt es wieder genau eine Funktion von
nach
, die ebenfalls leer ist. Diese Funktion ist injektiv aber nicht surjektiv. Sie besitzt weder Links- noch Rechtsinverse, da es überhaupt keine Funktionen von
nach
gibt.
- Bei der Einführung des Funktionsbegriffs in der Mathematik gibt es verschiedene Vorgehensweisen. Der in diesem Artikel verwendete Begriff der Surjektivität setzt voraus, dass die Zielmenge ein Teil der Identität der Funktion ist. Legt man einen anderen Funktionsbegriff zu Grunde, so muss man einige der Ausführungen entsprechend anpassen.
- Die meisten der Aussagen in diesem Artikel gelten auch für Funktionen zwischen Klassen.
Siehe auch
- Retraktion und Koretraktion, Links- bzw. Rechtsinverse in Kategorien


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 29.05. 2023