Ganze Zahl
steht für die Menge der ganzen Zahlen
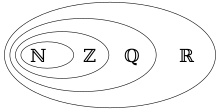
Die ganzen Zahlen (auch Ganzzahlen, lat. numeri integri) sind eine Erweiterung der natürlichen Zahlen.
Die ganzen Zahlen umfassen alle Zahlen
- …, −3, −2, −1, 0, 1, 2, 3, …
und enthalten damit alle natürlichen Zahlen
sowie deren additive
Inverse. Die Menge
der ganzen Zahlen wird meist mit dem Buchstaben
mit Doppelstrich
bezeichnet (das „Z“ steht für das deutsche Wort „Zahlen“). Das
alternative Symbol
ist mittlerweile weniger verbreitet; ein Nachteil dieses Fettdruck-Symbols ist
die schwierige handschriftliche Darstellbarkeit. Der Unicode
des Zeichens lautet U+2124 und hat die Gestalt ℤ.
Die obige Aufzählung der ganzen Zahlen gibt auch gleichzeitig in aufsteigender Folge deren natürliche Anordnung wieder. Die Zahlentheorie ist der Zweig der Mathematik, der sich mit Eigenschaften der ganzen Zahlen beschäftigt.
Die Repräsentation ganzer Zahlen im Computer erfolgt üblicherweise durch den Datentyp Integer.
Die ganzen Zahlen werden im Mathematikunterricht üblicherweise in der fünften bis siebten Klasse eingeführt.
Eigenschaften
Ring
Die ganzen Zahlen bilden einen Ring bezüglich der Addition und der Multiplikation, d.h., sie können ohne Einschränkung addiert, subtrahiert und multipliziert werden. Dabei gelten Rechenregeln wie das Kommutativgesetz und das Assoziativgesetz für Addition und Multiplikation, außerdem gelten die Distributivgesetze.
Durch die Existenz der Subtraktion können lineare Gleichungen der Form
mit natürlichen Zahlen
und
stets gelöst werden:
.
Beschränkt man
auf die Menge der natürlichen Zahlen, dann ist nicht jede solche Gleichung
lösbar.
Abstrakt
ausgedrückt heißt das, die ganzen Zahlen bilden einen kommutativen unitären
Ring. Das neutrale
Element der Addition ist 0, das additiv inverse
Element von
ist
,
das neutrale Element der Multiplikation ist 1.
Anordnung
Die Menge der ganzen Zahlen ist total geordnet, in der Reihenfolge
.
D.h., man kann je zwei ganze Zahlen vergleichen. Man spricht von positiven
,
nichtnegativen
,
negativen
und nichtpositiven
ganzen Zahlen. Die Zahl 0 selbst ist weder positiv noch negativ. Diese Ordnung
ist verträglich mit den Rechenoperationen, d.h.:
- Ist
und
, dann ist
.
- Ist
und
, dann ist
.
Mithilfe der Anordnung lassen sich die Vorzeichenfunktion
und die Betragsfunktion
definieren. Sie hängen wie folgt
zusammen.
Mächtigkeit
Wie die Menge der natürlichen Zahlen ist auch die Menge der ganzen Zahlen abzählbar.
Die ganzen Zahlen bilden keinen Körper,
denn z. B. ist die Gleichung
nicht in
lösbar. Der kleinste Körper, der
enthält, sind die rationalen
Zahlen
.
Euklidischer Ring
Eine wichtige Eigenschaft der ganzen Zahlen ist die Existenz einer Division mit Rest.
Aufgrund dieser Eigenschaft gibt es für zwei ganze Zahlen stets einen größten
gemeinsamen Teiler, den man mit dem Euklidischen
Algorithmus bestimmen kann. In der Mathematik wird
als euklidischer
Ring bezeichnet. Hieraus folgt auch der Satz
von der eindeutigen Primfaktorzerlegung
in
.
Konstruktion aus den natürlichen Zahlen
Ist die Menge der natürlichen Zahlen gegeben, dann lassen sich die ganzen Zahlen daraus als Zahlbereichserweiterung konstruieren:
Auf der Menge
aller Paare
natürlicher Zahlen wird folgende Äquivalenzrelation
definiert:
, falls
Die Addition und Multiplikation auf
wird definiert durch:
ist nun die Menge aller Äquivalenzklassen.
Die Addition und Multiplikation der Paare induzieren nun wohldefinierte Verknüpfungen
auf ,
mit denen
zu einem Ring wird.
Die übliche Ordnung der ganzen Zahlen ist definiert als
falls
.
Jede Äquivalenzklasse
hat im Fall
einen eindeutigen Repräsentanten der Form
,
wobei
,
und im Fall
einen eindeutigen Repräsentanten der Form
,
wobei
.
Die natürlichen Zahlen lassen sich in den Ring der ganzen Zahlen einbetten,
indem die natürliche Zahl
auf die durch
repräsentierte Äquivalenzklasse abgebildet wird. Üblicherweise werden die
natürlichen Zahlen mit ihren Bildern
identifiziert und die durch
repräsentierte Äquivalenzklasse wird mit
bezeichnet.
Ist
eine von
verschiedene natürliche Zahl, so wird die durch
repräsentierte Äquivalenzklasse als positive ganze Zahl und die durch
repräsentierte Äquivalenzklasse als negative ganze Zahl bezeichnet.
Diese Konstruktion der ganzen Zahlen aus den natürlichen Zahlen funktioniert
auch dann, wenn statt
die Menge
,
also ohne
,
als Ausgangsmenge genommen wird. Dann ist die natürliche Zahl
in der Äquivalenzklasse von
und die
>
in der von
.
Verwandte Themen
- Eine ähnliche Konstruktion wie die Konstruktion der ganzen Zahlen aus den
natürlichen Zahlen ist allgemein für kommutative
Halbgruppen möglich. In diesem Sinn ist
die Grothendieck-Gruppe von
.
- Die gaußschen Zahlen und die Eisenstein-Zahlen sind zwei verschiedene Erweiterungen der ganzen Zahlen zu Mengen komplexer Zahlen.
- Die proendliche
Vervollständigung der Gruppe
der ganzen Zahlen wird gebildet als (projektiver oder) inverser Limes aller endlichen Faktorgruppen von
und stellt die Gesamtheit der proendlichen ganzen Zahlen dar. Sie ist unter dem Symbol
bekannt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 18.03. 2023