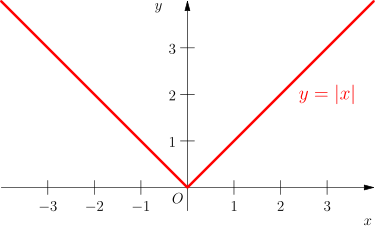
Betragsfunktion
In der Mathematik
ordnet die Betragsfunktion einer reellen
oder komplexen Zahl ihren
Abstand zur Null zu. Dieser sogenannte absolute Betrag, Absolutbetrag,
Absolutwert oder auch schlicht Betrag ist immer eine nichtnegative
reelle Zahl. Der Betrag einer Zahl
wird meist mit
,
seltener mit
,
bezeichnet. Das Quadrat der Betragsfunktion wird auch Betragsquadrat genannt.
Definition
Reelle Betragsfunktion
Den absoluten Betrag einer reellen Zahl erhält man durch Weglassen des Vorzeichens. Auf der Zahlengeraden bedeutet der Betrag den Abstand der gegebenen Zahl von Null.
Für eine reelle Zahl
gilt:
Komplexe Betragsfunktion
Für eine komplexe Zahl
mit reellen Zahlen
und
definiert man
,
wobei
die komplex
Konjugierte von
bezeichnet. Ist
reell (d.h.
,
also
),
so geht diese Definition in
über, was mit der Definition
des Betrages einer reellen Zahl
übereinstimmt.
Veranschaulicht man die komplexen Zahlen als Punkte der Gaußschen
Zahlenebene, so entspricht diese Definition nach dem Satz des Pythagoras
ebenfalls dem Abstand des zur Zahl
gehörenden Punktes vom sogenannten Nullpunkt.
Beispiele
Folgende Zahlenbeispiele zeigen die Funktionsweise der Betragsfunktion.
Gleichungen mit Absolutbetrag
Aus
folgt für reelle Zahlen
oder
.
Ist jedoch
,
dann ist
.
Als Beispiel sind alle Zahlen
gesucht, welche die Gleichung
erfüllen.
Man rechnet wie folgt:
Die Gleichung besitzt also genau zwei Lösungen für ,
nämlich 2 und −8.
Ungleichungen mit Absolutbetrag
Für Ungleichungen können die folgenden Äquivalenzen verwendet werden:
Gesucht seien beispielsweise alle Zahlen
mit der Eigenschaft
.
Dann rechnet man:
Als Lösung erhält man also alle
aus dem Intervall
.
Allgemein gilt für reelle Zahlen ,
und
:
.
Betragsnorm und Betragsmetrik
Die Betragsfunktion erfüllt die drei Normaxiome Definitheit, absolute Homogenität und Subadditivität und ist damit eine Norm, genannt Betragsnorm, auf dem Vektorraum der reellen oder komplexen Zahlen. Die Definitheit folgt daraus, dass die einzige Nullstelle der Wurzelfunktion im Nullpunkt liegt, womit
gilt. Die Homogenität folgt für komplexe
aus
und die Dreiecksungleichung aus
wobei sich die beiden gesuchten Eigenschaften jeweils durch Ziehen der (positiven) Wurzel auf beiden Seiten ergeben. Hierbei wurde genutzt, dass die Konjugierte der Summe bzw. des Produkts zweier komplexer Zahlen die Summe bzw. das Produkt der jeweils konjugierten Zahlen ist. Weiterhin wurde verwendet, dass die zweimalige Konjugation wieder die Ausgangszahl ergibt und dass der Betrag einer komplexen Zahl immer mindestens so groß wie ihr Realteil ist. Im reellen Fall folgen die drei Normeigenschaften analog durch Weglassen der Konjugation.
Die Betragsnorm ist vom Standardskalarprodukt
zweier reeller bzw. komplexer Zahlen
und
induziert.
Die Betragsnorm selbst induziert wiederum eine Metrik
(Abstandsfunktion), die Betragsmetrik
,
indem als Abstand der Zahlen der Betrag ihrer Differenz genommen wird.
Analytische Eigenschaften
In diesem Abschnitt werden Eigenschaften der Betragsfunktion angeführt, die insbesondere im mathematischen Bereich der Analysis von Interesse sind.
Nullstelle
Die einzige Nullstelle der beiden Betragsfunktionen ist 0, das heißt
gilt genau dann, wenn
gilt. Dies ist somit eine andere Terminologie
der zuvor erwähnten Definitheit.
Verhältnis zur Vorzeichenfunktion
Für alle
gilt
,
wobei
die Vorzeichenfunktion
bezeichnet. Da die reelle nur die Einschränkung
der komplexen Betragsfunktion auf
ist, gilt die Identität auch für die reelle Betragsfunktion. Die Ableitung der
auf
eingeschränkten Betragsfunktion ist die auf
eingeschränkte Vorzeichenfunktion.
Stetigkeit, Differenzierbarkeit und Integrierbarkeit
Die reelle Betragsfunktion
und die komplexe
sind auf ihrem ganzen Definitionsbereich
stetig.
Aus der Subadditivität der Betragsfunktion beziehungsweise aus der (umgekehrten)
Dreiecksungleichung folgt, dass die beiden Betragsfunktionen sogar Lipschitz-stetig sind
mit Lipschitz-Konstante
:
.
Die reelle Betragsfunktion ist an der Stelle
nicht differenzierbar
und somit auf ihrem Definitionsbereich
keine differenzierbare Funktion. Sie ist jedoch fast
überall differenzierbar, was auch aus dem Satz von Rademacher
folgt. Für
ist die Ableitung der reellen Betragsfunktion die Vorzeichenfunktion
.
Als stetige Funktion ist die reelle Betragsfunktion über beschränkte Intervalle
integrierbar;
eine Stammfunktion ist
.
Die komplexe Betragsfunktion
ist nirgends komplex
differenzierbar, denn die Cauchy-Riemann-Differentialgleichungen
sind nicht erfüllt.
Archimedischer Betrag
Beide Betragsfunktionen, die reelle und die komplexe, werden archimedisch
genannt, weil es eine ganze Zahl
gibt mit
.
Daraus folgt aber auch, dass für alle ganzen Zahlen
ebenfalls
ist.
Verallgemeinerungen
Betragsfunktion für Körper
Definition
Verallgemeinert spricht man von einem Betrag, wenn eine Funktion
von einem Integritätsbereich
in die reellen Zahlen
folgende Bedingungen erfüllt:
| (0) | Nicht-Negativität | ||
| (1) | Definitheit | ||
| (0) und (1) zusammen nennt man positive Definitheit | |||
| (2) | Multiplikativität, absolute Homogenität | ||
| (3) | Subadditivität, Dreiecksungleichung | ||
Die Fortsetzung
auf den Quotientenkörper
von
ist wegen der Multiplikativität eindeutig.
- Bemerkung
- Eine Betragsfunktion
für einen Körper ist eine Bewertung
dieses Körpers.
Ist
für alle natürlichen
,
dann nennt man den Betrag (oder die Bewertung) nichtarchimedisch.
Der Betrag
für alle
(ist nichtarchimedisch und) wird trivial genannt.
Bei nichtarchimedischen Beträgen (oder Bewertungen) gilt
| (3’) | die verschärfte Dreiecksungleichung. |
Sie macht den Betrag zu einem ultrametrischen. Umgekehrt ist jeder ultrametrische Betrag nichtarchimedisch.
Betrag und Charakteristik
- Integritätsbereiche mit einem archimedischen Betrag haben die Charakteristik 0.
- Integritätsbereiche mit einer von 0 verschiedenen Charakteristik (haben Primzahlcharakteristik und) nehmen nur nichtarchimedische Beträge an.
- Endliche Integritätsbereiche sind endliche Körper mit Primzahlcharakteristik und nehmen nur den trivialen Betrag an.
- Der Körper der rationalen Zahlen
als Primkörper der Charakteristik 0 und seine endlichen Erweiterungen nehmen sowohl archimedische als auch nichtarchimedische Beträge an.
Vervollständigung
Der Körper
lässt sich für jede Betragsfunktion, genauer: für die von jeder Betragsfunktion
(oder Bewertung) induzierte Metrik, vervollständigen.
Die Vervollständigung von
wird häufig mit
bezeichnet.
Archimedische Vervollständigungen der rationalen Zahlen
sind
und
,
nichtarchimedische sind
für Primzahlen
.
Beim trivialen Betrag entsteht nichts Neues.
Äquivalenz von Beträgen
Sind
und
Beträge (oder Bewertungen) eines Körpers
,
dann sind die folgenden drei Behauptungen gleichwertig:
- Jede Folge
, die unter
eine Nullfolge ist, d.h.
, ist auch unter
eine Nullfolge – und umgekehrt.
- Aus
folgt
.
ist eine Potenz von
, d.h.
für alle
mit einem festen
.
Die Betragsfunktionen der rationalen Zahlen
Nach dem Satz
von Ostrowski repräsentieren die in diesem Artikel erwähnten Beträge, der
eine archimedische (und euklidische) und die unendlich vielen je einer Primzahl
zuzuordnenden nichtarchimedischen, alle Klassen von Beträgen (oder Bewertungen)
der rationalen Zahlen .
Für diese Beträge gilt der Approximationssatz.
Norm
Die Betragsfunktion auf den reellen bzw. komplexen Zahlen kann durch die Eigenschaften Definitheit, absolute Homogenität und Subadditivität auf beliebige Vektorräume verallgemeinert werden. Eine solche Funktion wird Norm genannt. Sie ist aber nicht eindeutig bestimmt.
Pseudobetrag


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 21.06. 2021