Satz des Pythagoras
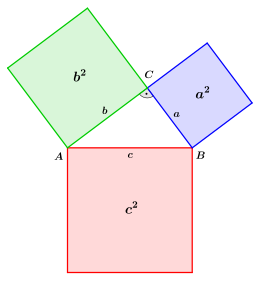
Der Satz des Pythagoras (auch Hypotenusensatz) ist einer der
fundamentalen Sätze
der euklidischen
Geometrie. Er besagt, dass in allen ebenen rechtwinkligen
Dreiecken die Summe der Flächeninhalte
der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrates ist. Sind
und
die Längen
der am rechten
Winkel anliegenden Seiten, der Katheten,
und
die Länge der dem rechten Winkel gegenüberliegenden Seite, der Hypotenuse dann lautet der
Satz als Gleichung ausgedrückt:
Der Satz ist nach Pythagoras von Samos benannt, der als Erster dafür einen mathematischen Beweis gefunden haben soll, was allerdings in der Forschung umstritten ist. Die Aussage des Satzes war schon lange vor der Zeit des Pythagoras in Babylon und Indien bekannt, es gibt jedoch keinen Nachweis dafür, dass man dort auch einen Beweis hatte.
Mathematische Aussage
Der Satz des Pythagoras lässt sich folgendermaßen formulieren:
- Sind
,
und
die Seitenlängen eines rechtwinkligen Dreiecks, wobei
und
die Längen der Katheten sind und
die Länge der Hypotenuse ist, so gilt
.
In geometrischer Deutung ist demnach in einem rechtwinkligen Dreieck die Summe der Flächen der beiden Quadrate über den Katheten gleich der Fläche des Quadrats über der Hypotenuse.
Die Umkehrung des Satzes gilt ebenso:
- Gilt die Gleichung
in einem Dreieck mit den Seitenlängen
,
und
, so ist dieses Dreieck rechtwinklig, wobei der rechte Winkel der Seite
gegenüberliegt.
Eng verwandt mit dem Satz des Pythagoras sind der Höhensatz und der Kathetensatz. Diese beiden Sätze und der Satz des Pythagoras bilden zusammen die Satzgruppe des Pythagoras. Der unten beschriebene Kosinussatz ist eine Verallgemeinerung des pythagoreischen Satzes.
Verwendung
Längen im rechtwinkligen Dreieck
Aus dem Satz des Pythagoras folgt direkt, dass die Länge der Hypotenuse gleich der Quadratwurzel aus der Summe der Kathetenquadrate ist, also
.
Eine einfache und wichtige Anwendung des Satzes ist, aus zwei bekannten Seiten eines rechtwinkligen Dreiecks die dritte zu berechnen. Dies ist durch Umformung der Gleichung für alle Seiten möglich:
Die Umkehrung des Satzes kann dazu verwendet werden, zu überprüfen, ob ein gegebenes Dreieck rechtwinklig ist. Dazu wird getestet, ob die Gleichung des Satzes für die Seiten bei dem gegebenen Dreieck zutrifft. Es reicht also allein die Kenntnis der Seitenlängen eines gegebenen Dreiecks, um daraus zu schließen, ob es rechtwinklig ist oder nicht:
- Sind die Seitenlängen z.B.
,
und
, dann ergibt sich
, und daher ist das Dreieck rechtwinklig.
- Sind die Seitenlängen z.B.
,
und
, dann ergibt sich
, und daher ist das Dreieck nicht rechtwinklig.
Aus dem Satz des Pythagoras folgt, dass in einem rechtwinkligen Dreieck die Hypotenuse länger als jede der Katheten und kürzer als deren Summe ist. Letzteres ergibt sich auch aus der Dreiecksungleichung.
Pythagoreische Tripel
Unter allen Dreiergruppen ,
die die Gleichung
erfüllen, gibt es unendlich viele, bei denen
,
und
jeweils ganze Zahlen sind. Diese
Dreiergruppen werden pythagoreische Tripel genannt. Das einfachste dieser Tripel
besteht aus den Zahlen
,
und
.
Pythagoreische Tripel werden seit alters her zur Konstruktion rechtwinkliger
Dreiecke verwendet. Ein Beispiel ist die Zwölfknotenschnur,
mit der ein Dreieck gelegt wird, dessen Seiten die Längen
,
und
haben. Die beiden kurzen Seiten bilden dann einen rechten Winkel.
Der große
fermatsche Satz besagt, dass die -te
Potenz einer Zahl, wenn
ist, nicht als Summe zweier Potenzen des gleichen Grades dargestellt werden
kann. Gemeint sind ganze Grundzahlen
und natürliche Hochzahlen. Allgemein gesprochen bedeutet dies:
- Die Gleichung
besitzt für ganzzahlige
und natürliche Zahlen
keine Lösung.
Das ist erstaunlich, weil es für
unendlich viele Lösungen gibt. Für
sind dies die pythagoreischen Zahlentripel.
Euklidischer Abstand
Der Satz von Pythagoras liefert eine Formel für den Abstand
zweier Punkte
in einem kartesischen
Koordinatensystem. Sind zwei Punkte
und
in einer Ebene
gegeben, dann ist ihr Abstand
durch
gegeben. Hierbei wird ausgenutzt, dass die Koordinatenachsen senkrecht zueinander liegen. Diese Formel kann auch auf mehr als zwei Dimensionen erweitert werden und liefert dann den euklidischen Abstand. Zum Beispiel gilt im dreidimensionalen euklidischen Raum
.
Beweise

Für den Satz sind mehrere hundert Beweise bekannt, womit er wohl der meistbewiesene mathematische Satz ist. Exemplarisch werden neben dem Beweis durch Addition abgeleiteter Volumina, aus dem Zhoubi suanjing (Arithmetischer Klassiker des Zhou-Gnomons), nachfolgend weitere vier geometrische Beweise vorgestellt.
Geometrischer Beweis durch Ergänzung
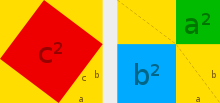
In ein Quadrat mit der Seitenlänge
werden vier kongruente
rechtwinklige Dreiecke mit den Seiten
,
und
(Hypotenuse) eingelegt. Dies kann auf zwei Arten geschehen, wie im Diagramm
dargestellt ist.
Die Flächen des linken und des rechten Quadrates sind gleich (Seitenlänge
).
Das linke besteht aus den vier rechtwinkligen Dreiecken und einem Quadrat mit
Seitenlänge
,
das rechte aus den gleichen Dreiecken sowie einem Quadrat mit Seitenlänge
und einem mit Seitenlänge
.
Die Fläche
entspricht also der Summe der Fläche
und der Fläche
,
also
.
Eine algebraische Lösung ergibt sich aus dem linken Bild des Diagramms. Das
große Quadrat hat die Seitenlänge
und somit die Fläche
.
Zieht man von dieser Fläche die vier Dreiecke ab, die jeweils eine Fläche von
(also insgesamt
)
haben, so bleibt die Fläche
übrig. Es ist also
.
Auflösen der Klammer liefert
.
Zieht man nun auf beiden Seiten
ab, bleibt der Satz des Pythagoras übrig.
Scherungsbeweis

Eine Möglichkeit ist die Scherung der Kathetenquadrate in das Hypotenusenquadrat. Unter Scherung eines Rechtecks versteht man in der Geometrie die Überführung des Rechtecks in ein Parallelogramm unter Beibehaltung der Höhe. Bei der Scherung ist das sich ergebende Parallelogramm zu dem Ausgangsrechteck flächengleich. Über zwei Scherungen können die beiden kleineren Quadrate dann in zwei Rechtecke umgewandelt werden, die zusammen genau in das große Quadrat passen.
Beim exakten Beweis muss dann noch über die Kongruenzsätze im
Dreieck nachgewiesen werden, dass die kleinere Seite der sich ergebenden
Rechtecke jeweils dem betreffenden Hypotenusenabschnitt entspricht. Wie üblich
wurden in der Animation die Höhe mit
und die Hypotenusenabschnitte mit
bezeichnet.
Beweis mit Ähnlichkeiten
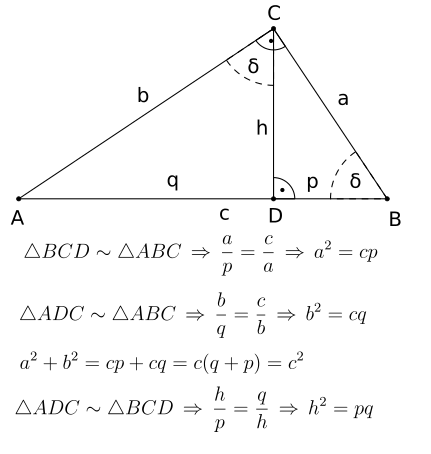
Es ist nicht unbedingt notwendig, zum Beweis des Satzes von Pythagoras
(explizit) Flächen heranzuziehen. Geometrisch eleganter ist es, Ähnlichkeiten zu
verwenden. Sobald man sich durch Berechnung der Winkelsummen im Dreieck
überzeugt hat, dass die beiden Winkel
im unteren Bild gleich groß sein müssen, sieht man, dass die Dreiecke
,
und
ähnlich sind. Der Beweis des Satzes von Pythagoras ergibt sich dann wie im Bild
gezeigt, dabei beweist man auch den Kathetensatz
und die Addition beider Varianten des Kathetensatzes ergibt den Satz des
Pythagoras selbst. Diese Herleitung lässt sich anschaulich mit der Ähnlichkeit
der Quadrate und der Ähnlichkeit deren angrenzenden Dreiecke erklären. Da deren
Fläche proportional zur Fläche der jeweils anliegenden Quadrate ist,
repräsentiert die Gleichung
den Satz.
Beweis der Umkehrung
Links: Gewähltes Ausgangsdreieck erfüllt
Rechts: Rechtwinkliges Dreieck, dessen Längen der Katheten entsprechen den Seitenlängen von
Die Umkehrung des Satzes lässt sich auf verschiedene Arten beweisen, ein besonders einfacher Beweis ergibt sich jedoch, wenn man den Satz des Pythagoras selbst zum Beweis seiner Umkehrung heranzieht.
Zu einem beliebigen Dreieck, dessen Seiten
die Bedingung
erfüllen, konstruiert man ein zweites Dreieck. Dieses besitzt einen rechten
Winkel, dessen Schenkellängen den Seitenlängen von
und
entsprechen. Nach dem Satz des Pythagoras beträgt nun die Länge der Hypotenuse
in diesem zweiten Dreieck
und entspricht damit der Länge der Seite
des Ausgangsdreiecks. Somit besitzen die beiden Dreiecke die gleichen
Seitenlängen und sind aufgrund des ersten Kongruenzsatzes
(SSS) kongruent. Damit sind dann aber auch ihre Winkel gleich, das heißt, auch
das Ausgangsdreieck besitzt einen rechten Winkel, der der Seite
gegenüberliegt.
Verallgemeinerungen und Abgrenzung
Kosinussatz
Der Kosinussatz ist eine Verallgemeinerung des Satzes von Pythagoras für beliebige Dreiecke:
,
wobei
der Winkel zwischen den Seiten
und
ist. Der Kosinussatz unterscheidet sich also durch den Term
vom Satz des Pythagoras. Da der Kosinus
von
gleich null ist, fällt dieser Term bei einem rechten Winkel weg, und es ergibt
sich als Spezialfall der Satz des Pythagoras. Gilt umgekehrt in einem Dreieck
die Beziehung
,
so muss
sein, woraus
folgt, und daher ist das Dreieck rechtwinklig. Für spitzwinklige
Dreiecke gilt entsprechend
und für stumpfwinklige Dreiecke
.
Verallgemeinerung von Thabit ibn Qurra
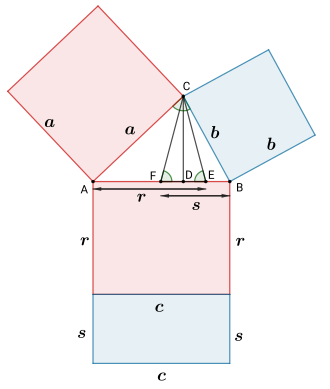
Gleichfarbige Rechtecke sind flächengleich,
gleichfarbige Winkel sind gleich groß,
Eine auf Thabit ibn Qurra zurückgehende Verallgemeinerung liefert zu den Quadraten über zwei Seiten eines beliebigen Dreiecks ein Rechteck über der dritten Seite, dessen Fläche der Summe der beiden Quadratflächen entspricht.
Zu einem beliebigen Dreieck
mit Seiten
,
Winkel
in
und Höhe
konstruiert man ein gleichschenkliges Dreieck
dessen Basis auf der Seite
liegt und das
als Höhe besitzt. Darüber hinaus besitzen seine beiden Basiswinkel die gleiche
Größe wie
,
sofern
ein spitzer Winkel ist. Ist
hingegen ein stumpfer Winkel, so sollen die Basiswnkel
betragen. Ferner wird der Eckpunkt des gleichschenkligen Dreiecks, der auf
derselben Seite von
wie
liegt, mit E bezeichnet und der andere Eckpunkt auf derselben Seite wie
mit
.
Dies gilt jedoch nur im Falle
,
für
vertauscht man stattdessen
und
.
Im Fall
fällt das gleichschenklige Dreieck mit der Höhe
zusammen und die Punkte
und
dementsprechend mit dem Punkt
.
Definiert man nun
und
,
so gilt:
Für
gilt dabei
und die obige Gleichung liefert den Satz des Pythagoras.
Die Aussage lässt sich analog zum Satz des Pythagoras direkt über ähnliche
Dreiecke beweisen, wobei hier die Dreiecke ,
und
ähnlich sind.
Aufgrund von
liefert Qurras Verallgemeinerung auch eine geometrische Darstellung des
Korrekturterms im Kosinussatz als ein Rechteck, das zu dem Quadrat über der
Seite
hinzugefügt oder von ihm abgetrennt wird, um eine Fläche zu erhalten, die der
Summe der Flächen der Quadrate über den Seiten
und
entspricht.
Flächensatz von Pappus
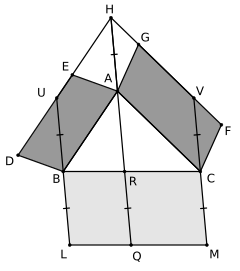
Eine weitere Verallgemeinerung auf beliebige Dreiecke liefert die Flächenformel von Pappus. Hier ergibt sich aus zwei beliebigen Parallelogrammen über zwei Seiten eines beliebigen Dreiecks ein eindeutig bestimmtes Parallelogramm über der dritten Seite des Dreiecks, dessen Fläche der Summe der Flächen der beiden Ausgangsparallelogramme entspricht. Sind die beiden Ausgangsparallelogramme Quadrate, so erhält man im Falle eines rechtwinkligen Dreiecks ein Quadrat über der dritten Seite und damit den Satz des Pythagoras.
Das Parallelogramm über der dritten Seiten erhält man, indem man die beiden Seiten der Ausgangsparallelogramme, die parallel zu den Dreiecksseiten sind, verlängert und deren Schnittpunkt mit dem Eckpunkt des Dreiecks, der auch auf beiden Parallelogrammen liegt, verbindet. Diese Verbindungsstrecke liefert das zweite Seitenpaar des Parallelogramms über der dritten Seite (siehe Zeichnung).
Ähnliche Figuren, errichtet über den Seiten des rechtwinkligen Dreiecks
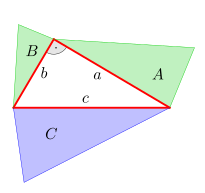
Es gilt:
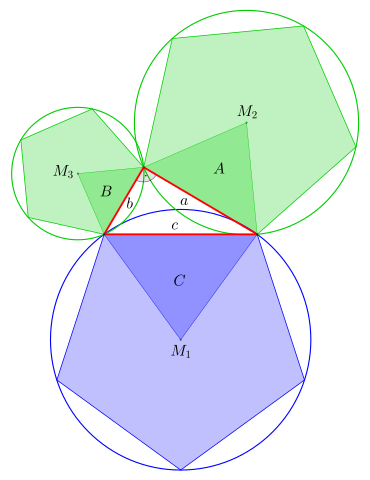
Es gilt jeweils:
Eine Verallgemeinerung des Satzes des Pythagoras mithilfe von drei zueinander ähnlichen Figuren über den Dreieckseiten (neben den bereits bekannten Quadraten) war bereits Hippokrates von Chios im 5. Jahrhundert v.Chr. bekannt und wurde, wahrscheinlich zweihundert Jahre später, von Euklid in seinem Werk Elemente aufgenommen:
„Im rechtwinkligen Dreieck ist die gradlinige Figur über der Hypotenuse gleich den ähnlichen und ähnlich errichteten Figuren über den Katheten zusammen.“
Errichtet man über den drei Seiten
und
des ursprünglichen Dreiecks jeweils eine zu den beiden anderen ähnliche Figur
(Bild 1) mit den Flächen
und
dann gilt wegen ihrer Ähnlichkeit:
Stellt man
und
in der Form
dar, so erhält man für die Summe:
Nach dem Satz des Pythagoras
wird
für
eingesetzt und somit ergibt sich:
Während Euklids Beweis nur für konvexe
Polygone
(Vielecke) gilt,
ist der Satz auch für konkave Polygone und sogar für ähnliche Figuren mit
gekrümmten Grenzen gültig, wobei auch diese Figuren aus einer betreffenden Seite
des ursprünglichen Dreiecks hervorgehen.
Die im Bild 2 dargestellten Flächen
und
der Kreise
entstehen aus den Seiten
und
der Fünfecke.
Um zu verdeutlichen, dass Kreise bzw. Halbkreise
allein, d.h. ohne Vielecke über den Seiten, zur Verallgemeinerung
herangezogen werden können, erweitert man den Satz des Pythagoras mit der Kreiszahl
Aus dem Satz mit Quadraten
wird, mit den entsprechenden Seitenlängen
und
als Radien, eine Verallgemeinerung mit Kreisen
bzw. eine Verallgemeinerung mit Halbkreisen:
Die Grundidee hinter dieser Verallgemeinerung ist, dass die Fläche einer ebenen Figur proportional zum Quadrat jeder linearen Dimension und insbesondere proportional zum Quadrat der Länge jeder Seite ist.
Skalarprodukträume
Abstrahiert man vom gewöhnlichen euklidischen Raum zu allgemeinen Skalarprodukträumen, also Vektorräumen mit einem Skalarprodukt, dann gilt:
Sind zwei Vektoren
und
zueinander orthogonal,
ist also ihr Skalarprodukt
,
dann gilt aufgrund der Linearität
des Skalarprodukts
,
wobei
die von dem Skalarprodukt induzierte
Norm bezeichnet.
Bezieht man diesen Satz wiederum auf den euklidischen Raum, dann stehen
und
für die Katheten
und
eines rechtwinkligen Dreiecks.
steht für die Länge der Hypotenuse
.
Diese Verallgemeinerung des Satzes des Pythagoras findet sich auch in
abstrakten mathematischen Strukturen, etwa unendlichdimensionalen
Funktionenräumen wieder. Die Umkehrung gilt ebenfalls. Trifft die Gleichung zu,
so sind die beiden Vektoren orthogonal zueinander. Der Satz lässt sich noch
weiter verallgemeinern. Ist
ein Orthogonalsystem
bestehend aus paarweise orthogonalen Vektoren
,
dann folgt durch wiederholte Anwendung obigen Arguments:
Die entsprechende Aussage gilt sogar für unendliche Summen, wenn man eine Folge
von Vektoren betrachtet, die alle zueinander orthogonal sind. Konvergiert nun
die Reihe
,
so konvergiert auch
und es gilt:
Der Beweis der zweiten Behauptung folgt dabei aus der Stetigkeit des Skalarprodukts. Eine weitere Verallgemeinerung führt zur Parsevalschen Gleichung.
Weitere Verallgemeinerungen
Ebenfalls als Verallgemeinerungen des Satzes des Pythagoras können der Schenkeltransversalensatz, der Satz von Stewart, der Satz von Ptolemäus und der Satz von der britischen Flagge gelten. Letzterer stellt sowohl eine Verallgemeinerung in der Ebene als auch im Raum dar. Die pythagoreische Gleichung ist darüber hinaus auch in der Apollonios-Gleichung enthalten.
Ein räumliches Analogon ist der Satz von de Gua. Hier werden das rechtwinklige Dreieck durch ein rechtwinkliges Tetraeder und die Seitenlängen durch die Flächeninhalte der Seitenflächen ersetzt. Sowohl der Satz des Pythagoras als auch der Satz von de Gua sind Spezialfälle eines allgemeinen Satzes über n-Simplexe mit einer rechtwinkligen Ecke.
Unterschiede in der nichteuklidischen Geometrie
Nichteuklidische Geometrien sind Geometrien, in denen das Parallelenaxiom nicht gilt. Ein Beispiel hierfür ist die Geometrie der Kugeloberfläche. Dort gilt der Satz des Pythagoras nicht mehr, da in solchen Geometrien der Innenwinkelsatz nicht gilt, also die Winkelsumme eines Dreiecks von 180° verschieden ist. Ein anderes Beispiel ist der „gekrümmte“ Raum der Allgemeinen Relativitätstheorie Albert Einsteins.
Geschichte
Babylon und Indien

Bereits auf einer babylonischen Keilschrifttafel, die in die Zeit der Hammurabi-Dynastie datiert wird (ca. 1829 bis ca. 1530 v.Chr.), findet sich eine geometrische Problemstellung mit Lösung, bei der der Satz zur Berechnung von Längen (im Sexagesimalsystem) verwendet wurde:
Ein Balken, 0;30 (= 30/60 GAR = 1/2 GAR ≈ 3 m lang)
Von oben ist er 0;6 (= 6/60 GAR) herabgekommen.
Von unten was hat er sich
entfernt?
0;30 (= 30/60) quadriere, 0;15 (= 900/3600 = 15/60) siehst du.
0;6 (= 6/60) von 0;30 (= 30/60) abgezogen, 0;24 (= 24/60) siehst du.
0;24 (=
24/60) quadriere, 0;9,36 (= 576/3600) siehst du.
0;9,36 (= 576/3600) von 0;15
(= 900/3600) ziehe ab, 0;5,24 (= 324/3600) siehst du.
0;5,24 (= 324/3600) hat
was als Quadratwurzel? 0;18 (= 18/60).
0;18 (= 18/60 GAR) am Boden hat er
sich entfernt.
Daraus ergibt sich:
, also
und weiter
.
Ein Interesse der Babylonier an einem mathematischen Beweis geht jedoch aus den Quellen nicht hervor.
Die Keilschrifttafel Plimpton 322 enthält außerdem
verschiedene pythagoreische Tripel, unter anderem
,
sowie
,
was auf ein Verfahren zur Berechnung solcher Tripel schließen lässt.
In indischen Sulbasutras („Schurregeln“ bzw. „Leitfäden zur Meßkunst“), die ungefähr vom 6. bis zum 4. Jahrhundert v.Chr. entstanden, finden sich einige pythagoreische Tripel. Außerdem wurde auch der Lehrsatz dort schon allgemein ausgesprochen und benutzt. Wie er begründet wurde, ist nicht sicher.
China
Der Satz war im antiken China als Satz der Gougu (勾股定理) bekannt. In der Schrift Zhoubi suanjing („Arithmetischer Klassiker des Zhou-Gnomons“), die ungefähr vom 1. Jahrhundert v.Chr. bis zum 6. Jahrhundert n.Chr. entstand, wird mit der sogenannten „Hypotenusen-Figur“ (Xian-tu) ein dort am Beispiel des rechtwinkligen Dreiecks (gougu) mit den Seiten 3, 4 und 5 gegebener Beweis des Satzes veranschaulicht. Auch im Jiu Zhang Suanshu („Neun Bücher arithmetischer Technik“, 1. Jahrhundert n.Chr.), dem klassischen mathematischen Werk Chinas mit einer Sammlung von 263 Problemstellungen, ihren Lösungen und den Lösungswegen, wird er angewendet. Liu Hui (3. Jahrhundert n.Chr.) gab wohl in seinem Kommentar zu den „Neun Büchern“ im neunten Kapitel einen Zerlegungsbeweis an.
Die umstrittene Rolle des Pythagoras

Die Benennung des Satzes nach dem griechischen Philosophen Pythagoras (6. Jahrhundert v.Chr.) ist erst in späten Quellen bezeugt. Daher ist in der Forschung die Frage nach der Rolle des Pythagoras stark umstritten. Verschiedene Hypothesen kommen in Betracht:
- Pythagoras übernahm den Satz von den Babyloniern, seine Rolle war nur die eines Vermittlers orientalischen Wissens an die Griechen. Antiken Quellen zufolge unternahm er eine Ägyptenreise, er soll sogar in Babylonien gewesen sein, doch ist die Glaubwürdigkeit der Berichte über seine Reisen umstritten.
- Pythagoras hat den Satz unabhängig von der orientalischen Mathematik entdeckt und auch erstmals bewiesen. Diese Ansicht war in der Antike verbreitet.
- Pythagoras verdankte die Kenntnis des Sachverhalts orientalischen Quellen, war aber der erste, der einen Beweis dafür fand. Tatsächlich waren Babylonier und Ägypter anscheinend nur an der Anwendung des Satzes für praktische Zwecke, nicht an einem allgemeingültigen Beweis interessiert. So enthält beispielsweise das älteste bekannte Rechenbuch der Welt, das ägyptische Rechenbuch des Ahmes (auch Papyrus Rhind) aus dem 17. Jahrhundert v.Chr., bereits komplizierte Aufgaben, es fehlt jedoch jede Verallgemeinerung, es wird nicht definiert und bewiesen.
- Pythagoras hat in der Geschichte des Satzes keine Rolle gespielt; erst spätere Pythagoreer haben möglicherweise den ersten Beweis gefunden.
Gegensätzliche Positionen vertreten die Wissenschaftshistoriker Walter Burkert und Leonid Zhmud. Burkert zieht allenfalls eine Vermittlerrolle des Pythagoras in Betracht, Zhmud schreibt ihm mathematische Leistungen wie den Beweis des Satzes zu und betont seine Eigenständigkeit gegenüber der orientalischen Mathematik.
Euklid, der in der zweiten Hälfte des 4. Jahrhunderts v.Chr. in seinem berühmten Werk Elemente das mathematische Wissen seiner Zeit zusammentrug, bot einen Beweis, brachte den Satz aber nicht mit Pythagoras in Zusammenhang. Der älteste Beleg dafür, dass der Satz mit Pythagoras in Verbindung gebracht wurde, ist ein Epigramm eines Apollodoros, der möglicherweise mit dem Philosophen Apollodoros von Kyzikos zu identifizieren ist; in diesem Fall stammen die Verse aus der zweiten Hälfte des 4. Jahrhunderts v.Chr. Der Text lautet:
Als Pythagoras einst die berühmte Zeichnung gefunden,
Brachte als Opfer er
dar herrliche Stiere dem Gott.
Apollodoros gibt nicht an, welche „berühmte“ Zeichnung oder Figur er meint, doch spätere Autoren, darunter Diogenes Laertios, der im 3. Jahrhundert die beiden Verse zitierte, gingen davon aus, dass es sich um den „Satz des Pythagoras“ handelt. Diese Überlieferung, wonach Pythagoras einem Gott zum Dank dafür, dass dieser ihm die Erkenntnis eingab, ein Rinderopfer darbrachte, steht in Widerspruch zu dem von zahlreichen antiken Quellen überlieferten Umstand, dass Pythagoras und die Pythagoreer Tieropfer grundsätzlich ablehnten.
Veranschaulichung
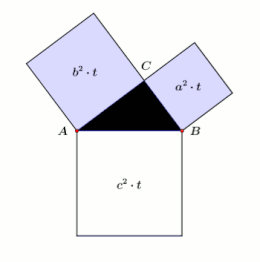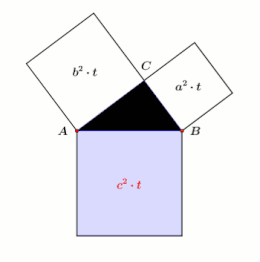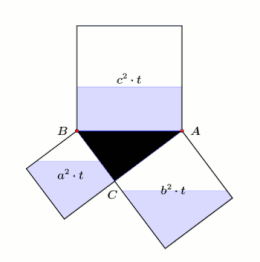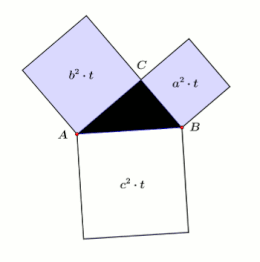
Sehr verbreitet sind Anschauungsobjekte, die mit Hilfe von Flüssigkeiten den
Satz des Pythagoras beschreiben. Die nebenstehende animierte Prinzipskizze ist quasi
die Vorderansicht eines drehbar gelagerten Exponates des Science-Center
Phaeno in Wolfsburg.
An den Seiten des mittigen rechtwinkligen Dreiecks sind flache durchsichtige
Behälter mit der Tiefe
angebracht. Deren quadratische Grundflächen sind gleich den Flächen der
Kathetenquadrate bzw. des Hypotenusenquadrates. Die Behälter sind deshalb mit
,
und
bezeichnet. Ist das Exponat in seiner Ausgangsstellung (
unten), fließt das in
und
randvoll gefüllte blaue Wasser über die Ecken des Dreiecks
und
restlos ab und füllt somit vollständig
.
Daraus folgt
,
geteilt durch
ergibt es
Verwandte Themen
- Pythagoreische Addition – die Wurzel aus der Summe der Quadrate mehrerer Werte
- Trigonometrischer Pythagoras – die Übertragung des Satzes auf die Winkelfunktionen Sinus und Cosinus
Literatur
- Anna M. Fraedrich: Die Satzgruppe des Pythagoras. Spektrum Akademischer Verlag, Heidelberg 1994, ISBN 3-86025-669-6.
- Hans Schupp: Elementargeometrie. UTB, Stuttgart 1977, ISBN 3-506-99189-2, S. 114–118.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.01. 2022