Pythagoreisches Tripel

Die Tontafel Plimpton 322

x und y von -1000 bis +1000

In der Zahlentheorie wird ein pythagoreisches Tripel oder pythagoreisches Zahlentripel von drei natürlichen Zahlen gebildet, die als Längen der Seiten eines rechtwinkeligen Dreiecks vorkommen können.

Sie finden sich bereits auf babylonischen Tontafeln, die in die Zeit der Hammurabi-Dynastie datiert werden (1829 bis 1530 v. Chr). Die Keilschrifttafel Plimpton 322 enthält 15 verschiedene pythagoreische Tripel, u.a. (56,90,106) , (119,120,169) und (12709,13500,18541) , was darauf schließen lässt, dass bereits vor mehr als 3500 Jahren ein Verfahren zur Berechnung solcher Tripel bekannt gewesen sein muss.

Das indische Baudhayana-Sulbasutra aus dem 6. Jahrhundert vor Christus enthält fünf pythagoreische Tripel.

Pythagoreische Tripel wurden auch von Diophant behandelt. Wegen des pythagoreischen Lehrsatzes sind sie genau die positiven ganzzahligen Lösungen der diophantischen Gleichung

$x^{2}+y^{2}=z^{2}$ .

Wenn , und keinen gemeinsamen Teiler haben, spricht man von einem primitiven pythagoreischen Tripel. Bei jedem primitiven Tripel ist ungerade, und von den Zahlen und ist eine gerade und die andere ungerade.

Beispiele

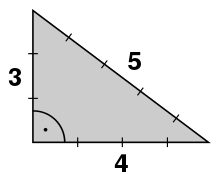
Das kleinste pythagoreische Tripel ist (3,4,5). Es ist primitiv. Es wird in der Zwölfknotenschnur zur Herstellung eines rechten Winkels benutzt.
Weitere kleine primitive pythagoreische Tripel sind (5,12,13) und (8,15,17).
(15,20,25) = (5·3,5·4,5·5) und (15,36,39) = (3·5,3·12,3·13) sind nicht primitiv.

Erzeugung der pythagoreischen Tripel

Die Formeln^[1]

$x=u^{2}-v^{2},y=2uv,z=u^{2}+v^{2}$

liefern für beliebige $u,v\in \mathbb {N} ,u>v$ ein pythagoreisches Tripel. Es ist genau dann primitiv, wenn und teilerfremd sind und u+v ungerade ist.

Umgekehrt lässt sich jedes primitive Tripel mit Hilfe dieser Formeln aus teilerfremden $u,v\in \mathbb {N}$ erzeugen. Dieses Resultat taucht schon in Euklids Elementen auf.

Jedes pythagoreische Tripel (X,Y,Z) kann aus einem primitiven Tripel (x,y,z) als (X = nx, Y = ny, Z = nz) mit einer ganzen Zahl n größer als null berechnet werden. Die natürliche Zahl n ist der größte gemeinsame Teiler von X, Y, Z und damit eindeutig bestimmt.

Beispiele:

u = 2, v = 1 liefert das Tripel (3,4,5).
Multiplikation mit 2 liefert (6,8,10). Es ergibt sich nach den „indischen Formeln“ aus u = 3, v = 1. Weil 3 und 1 beide ungerade sind, ist es trotzdem nicht primitiv.
u = 3, v = 2 liefert das primitive Tripel (5,12,13).
Multiplikation mit 7 liefert (35,84,91); dies ist ein pythagoreisches Tripel, das sich nicht nach den „indischen Formeln“ erzeugen lässt. Diese erzeugen nämlich alle primitiven, aber nur einen Teil der nicht-primitiven Tripel.

Herleitung der Formel zur Bildung der pythagoreischen Tripel

Ist (X,Y,Z) ein pythagoreisches Tripel, so ergibt die Division der zugehörigen Gleichung $X^{2}+Y^{2}=Z^{2}$ durch $Z^{2}$

${\frac {X^{2}}{Z^{2}}}+{\frac {Y^{2}}{Z^{2}}}=1.$

Die Zahlen $x={\tfrac {X}{Z}}$ und $y={\tfrac {Y}{Z}}$ sind rational und positiv und erfüllen die Koordinatengleichung des Einheitskreises

$x^{2}+y^{2}=1.$

Also ist (x,y) ein Punkt mit rationalen Koordinaten auf dem Einheitskreis. Die Gerade durch die Punkte (-1,0) und (x,y) schneidet die y-Achse im Punkt (0,t) . Für die Steigung dieser Gerade gilt

$t={\frac {y}{x+1}}={\frac {v}{u}}$ ,

wobei eine rationale Zahl ist und $u,\ v$ teilerfremde natürliche Zahlen sind.

Setzt man diese Gleichung in die Gleichung des Einheitskreises ein, erhält man:

$1=x^{2}+y^{2}=x^{2}+t^{2}(x+1)^{2},$

also

$0=(x^{2}-1)+t^{2}(x+1)^{2}=(x+1)[(x-1)+t^{2}(x+1)]$ .

Da die erste Lösung x=-1 wegen x<0 nicht interessiert, folgt:

$(x-1)+t^{2}(x+1)=0$

$x={\frac {1-t^{2}}{1+t^{2}}}$

$y=t\cdot (x+1)=t\cdot \left({\frac {1-t^{2}}{1+t^{2}}}+1\right)={\frac {2t}{1+t^{2}}}$

Die Koordinaten (x,y) sind damit:

$(x,y)=\left({\frac {1-t^{2}}{1+t^{2}}},{\frac {2t}{1+t^{2}}}\right)$

oder

$\left({\frac {X}{Z}},{\frac {Y}{Z}}\right)=\left({\frac {1-v^{2}/u^{2}}{1+v^{2}/u^{2}}},{\frac {2v/u}{1+v^{2}/u^{2}}}\right)=\left({\frac {u^{2}-v^{2}}{u^{2}+v^{2}}},{\frac {2uv}{u^{2}+v^{2}}}\right)$

Damit erhält man das pythagoreische Tripel:

$(X,Y,Z)=(u^{2}-v^{2},2uv,u^{2}+v^{2})$

Es kann vorkommen, dass $u^{2}-v^{2}$ , 2uv und $u^{2}+v^{2}$ einen gemeinsamen Teiler besitzen. Aus u=3,v=1 würde beispielsweise

folgen.

Als einzige Möglichkeit hierfür kommt jedoch D=2 in Betracht, denn angenommen, eine Primzahl teilte sowohl $u^{2}-v^{2}$ als auch $u^{2}+v^{2}$ , so gilt

$u^{2}\equiv v^{2}{\pmod {p}}$ und $u^{2}\equiv -v^{2}{\pmod {p}}$ ,

woraus man

$u^{2}\equiv -u^{2}{\pmod {p}}$

schließen kann. Aufgrund der Teilerfremdheit von und ist $u^{2}\equiv 0{\pmod {p}}$ , woraus sich $u\equiv v\equiv 0{\pmod {p}}$ ergeben würde, nicht möglich, und es bleibt p=2 zusammen mit $u\equiv v\equiv 1{\pmod {2}}$ als einzige Lösungsmöglichkeit.

Man kann solche u,v , die teilerfremd und beide ungerade sind, jedoch aussortieren, ohne primitive pythagoreische Tripel zu verlieren, denn wenn und das Tripel (2a,2b,2c) ergeben, so ergeben u'=(u+v)/2 und v'=(u-v)/2 das Tripel (b,a,c) , u',v' sind teilerfremd, und sie sind nicht beide ungerade.

Die ersten primitiven pythagoreischen Tripel

Nach diesen Regeln erhält man als primitive pythagoreische Tripel zum Beispiel (geordnet nach u+v):

u	v	x	y	z
2	1	3	4	5
4	1	15	8	17
3	2	5	12	13
6	1	35	12	37
5	2	21	20	29
4	3	7	24	25
8	1	63	16	65
7	2	45	28	53
5	4	9	40	41
10	1	99	20	101
9	2	77	36	85
8	3	55	48	73
7	4	33	56	65
6	5	11	60	61

Zwei Folgen von pythagoreischen Tripeln sind noch bemerkenswert:

für v = u-1:
(3, 4, 5), (5, 12, 13), (7, 24, 25), (9, 40, 41), (11, 60, 61), (13, 84, 85), …, (2n+1, 2n²+2n, 2n²+2n+1), …^[2]
, also für jede ungerade Zahl 2n+1 (außer 1) ein Tripel, bei dem die Zahl die kleinste Zahl ist und sich die beiden anderen Zahlen um genau 1 unterscheiden: x = 2n+1; y, z = x²/2 ± ½. Dies hängt damit zusammen, dass gemäß der ersten binomischen Formel (m+1)² = m²+2m+1 ist und deshalb jede ungerade Zahl 2m+1 die Differenz zweier Quadratzahlen ist. Da das Quadrat einer ungeraden Zahl 2n+1 auch ungerade ist, gibt es zu jeder ungeraden Zahl 2n+1 ein pythagoreisches Tripel (2m+1 = (2n+1)²).
für v = 1 (und gerades u):
(3, 4, 5), (15, 8, 17), (35, 12, 37), (63, 16, 65), (99, 20, 101), (143, 24, 145),…, (4n²-1, 4n, 4n²+1), …
also für jede natürliche Zahl ein Tripel, das die Zahl enthält, und bei dem sich die beiden anderen Zahlen um genau 2 unterscheiden: x = 4n; y, z = x²/4 ± 1. Auch dieses ergibt sich aus der ersten binomischen Formel: (m+2)² = m²+4m+4. Jede durch 16 teilbare Quadratzahl lässt sich als 4m+4 schreiben, sodass zu jeder Zahl 4n ein pythagoreisches Tripel existiert (4m+4 = (4n)²).

Auch für jede gerade Zahl x größer als 2, die kein Vielfaches von 4 ist, kann man mit der ersten Folge ein pythagoreisches Tripel bilden (2n+1 = x/2) und die Zahlen dann verdoppeln. Somit kann man zu jeder natürlichen Zahl x, die größer als 2 ist, ein Zahlenpaar y, z finden, welches sich bei ungeradem x um 1, bei geradem x um 2 unterscheidet:

x	y	z
3	4	5
4*	3	5
5	12	13
6*	8	10
7	24	25
8	15	17
9	40	41
10*	24	26
11	60	61
12	35	37
13	84	85
14*	48	50
15	112	113
16	63	65
17	144	145
18*	80	82
19	180	181
20	99	101

* nicht primitive Tripel. Die Fälle für x=4n+2 sind redundant, da sie eine Verdoppelung von x=2n+1 darstellen.

Zusammenhang mit den heronischen Dreiecken

Jedes zu einem pythagoreischen Tripel gehörige Dreieck ist ein heronisches Dreieck, das heißt, sowohl die Seitenlängen als auch der Flächeninhalt sind rationale Zahlen. Jedes heronische Dreieck lässt sich in zwei rechtwinklige Dreiecke zerlegen, die durch pythagoreische Tripel aus rationalen Zahlen gegeben sind.

Die Fermatsche Gleichung

Eine Verallgemeinerung der pythagoreischen Tripel erhält man, wenn man den Exponenten 2 durch eine natürliche Zahl ersetzt. Man untersucht also die diophantische Gleichung

$x^{n}+y^{n}=z^{n}\qquad (2<n\in \mathbb {N} )$

und sucht nach Lösungen durch natürliche (oder ganze) Zahlen $x,\ y,\ z$ unter Ausschluss der trivialen Lösungen, bei denen eine der drei Zahlen gleich Null ist.

Pierre de Fermat stellte um das Jahr 1637 die Behauptung auf, dass es keine derartigen Tripel gibt. Obwohl er keinen Beweis angab, wird diese Vermutung als großer Fermatscher Satz bezeichnet. Jahrhundertelang konnte kein Beweis gefunden werden. Die Suche danach führte aber zu vielen interessanten Ergebnissen, insbesondere in der Zahlentheorie. 1995 konnte der Mathematiker Andrew Wiles den Satz von Fermat schließlich beweisen.

Er erstellt für eine natürliche Zahl alle möglichen Tripel, deren Hypotenuse nicht überschreitet.

Anmerkung

↑ Diese Formeln werden auch indische Formeln genannt, da sie explizit schon von dem indischen Mathematiker Brahmagupta (598–668) angegeben werden;
↑ Die letztgenannte Formel nennt schon Pythagoras (etwa 570–510 v. Chr.);

Basierend auf einem Artikel in:

Wikipedia.de