Einheitskreis

In der Mathematik ist der
Einheitskreis der Kreis,
dessen Radius
die Länge 1 hat und dessen Mittelpunkt mit dem Koordinatenursprung
eines kartesischen
Koordinatensystems der Ebene übereinstimmt. Der Einheitskreis besteht also
aus den Punkten
der Ebene, für die
gilt.
Trigonometrische Zusammenhänge
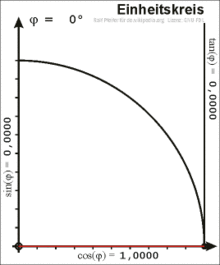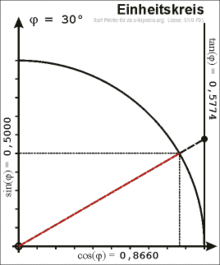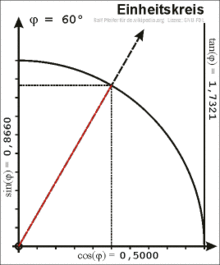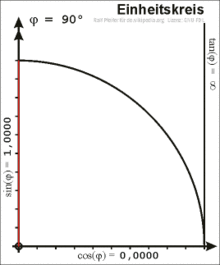
Liegt ein Punkt
auf
dem Einheitskreis, dann kann man einen Winkel
zu der x-Achse
(Abszisse) definieren, unter dem
vom Ursprung des Koordinatensystems aus gesehen wird. Für die Koordinaten
von
gilt dann
,
und
Unter Zuhilfenahme der Beziehungen im rechtwinkligen Dreieck lassen sich folgende Zusammenhänge aufstellen:
Außerdem existieren noch die wenig gebräuchlichen Funktionen Sekans und Kosekans, die definiert sind als die Kehrwertfunktionen von Kosinus und Sinus.
Die orientierte Länge der Tangente
an den Kreis, welche senkrecht auf der x-Achse steht, bis zum Scheitelpunkt
des Winkels ist der Tangens
von
alt="\varphi " src="/svg/33ee699558d09cf9d653f6351f9fda0b2f4aaa3e.svg".
Der Einheitskreis kann auch über die Eulersche Identität dargestellt werden:
.
Rationale Parametrisierung
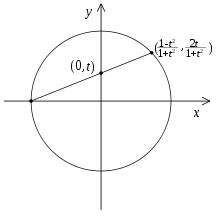
Auch ohne Rückgriff auf trigonometrische
Funktionen lassen sich alle Punkte des Einheitskreises finden. Sei
eine beliebige reelle Zahl. Ein Schnittpunkt der Geraden durch
und
mit dem Einheitskreis ist trivialerweise
.
Der andere befindet sich bei
,
und durchläuft, wenn
ganz
durchläuft, den ganzen Kreis. Der Punkt
wird dabei allerdings nur nach dem Grenzübergang
erreicht.
Diese Parametrisierung ist für alle Körper geeignet. Für rationale
erhält man aus ihr durch elementare Umformungen pythagoräische
Tripel
.
Andere Normen
Wird eine andere Norm
als die euklidische
Norm zur Abstandsmessung benutzt, so ist die Form des Einheitskreises im
kartesischen Koordinatensystem eine andere. So ist zum Beispiel der
Einheitskreis für die Maximumsnorm
ein Quadrat mit den Ecken
und der Einheitskreis für die Summennorm
ein Quadrat mit den Ecken
und
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.07. 2020