Kehrwert
Der Kehrwert (auch der reziproke Wert oder das
Reziproke) einer von
verschiedenen Zahl
ist in der Arithmetik diejenige Zahl,
die mit
multipliziert die Zahl
ergibt; er wird als
oder
notiert.
Eigenschaften
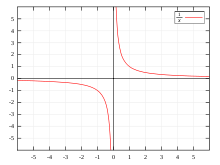
Je näher eine Zahl bei
liegt, desto weiter ist ihr Kehrwert von
entfernt. Die Zahl
selbst hat keinen Kehrwert und ist auch kein Kehrwert. Die durch
beschriebene Kehrwertfunktion (siehe Abbildung) hat dort eine Polstelle. Der Kehrwert einer
positiven Zahl ist positiv, der Kehrwert einer negativen Zahl ist negativ. Dies
findet seinen geometrischen Ausdruck darin, dass der Graph in zwei Hyperbeläste
zerfällt, die im ersten bzw. dritten Quadranten liegen. Die Kehrwertfunktion ist
eine Involution,
d.h. der Kehrwert des Kehrwerts von
ist wieder
Ist eine Größe
umgekehrt
proportional zu einer Größe
dann ist sie proportional zum Kehrwert von
Den Kehrbruch eines Bruches,
also den Kehrwert eines Quotienten
mit
erhält man, indem man Zähler und Nenner miteinander vertauscht:
Daraus folgt die Rechenregel für das Dividieren durch einen Bruch: Durch einen Bruch wird dividiert, indem man mit seinem Kehrwert multipliziert.
Den Kehrwert
einer natürlichen
Zahl
nennt man einen Stammbruch.
Auch zu jeder von
verschiedenen komplexen
Zahl
mit reellen Zahlen
gibt es einen Kehrwert
Mit dem Absolutbetrag
von
und der zu
konjugiert
komplexen Zahl
gilt:
Beispiele
- Der Kehrwert von 1 ist wiederum 1.
- Der Kehrwert von 0,001 ist 1000.
- Der Kehrwert von
ist
- Der Kehrwert des Bruches
ist
- Der Kehrwert der komplexen Zahl
ist
.
Verallgemeinerung
Eine Verallgemeinerung des Kehrwerts ist das multiplikativ Inverse
zu einer Einheit
eines unitären
Ringes. Es ist ebenfalls durch die Eigenschaft
definiert, wobei
das Einselement des Ringes bezeichnet.
Wenn es sich z.B. um einen Ring von Matrizen handelt, so ist das
Einselement nicht die Zahl
sondern die Einheitsmatrix.
Matrizen, zu denen keine inverse
Matrix existiert, heißen singulär.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 21.07. 2020