
Diophantische Gleichung
In der algebraischen Zahlentheorie ist eine diophantische Gleichung eine Gleichung der Form
,
wobei eine gegebene
Polynomfunktion mit ganzzahligen
Koeffizienten ist und nur ganzzahlige Lösungen für
gesucht werden.
Diese Gleichungen sind nach dem griechischen Mathematiker Diophantos von Alexandria
(mutmaßlich um 250) benannt.
Gleichungen dieser Art ergeben sich, wenn Teilbarkeitsfragen beantwortet werden sollen, wenn es sich um Probleme der Kongruenzarithmetik handelt oder wenn bei Problemen in der Praxis nur ganzzahlige Lösungen sinnvoll sind, z. B. für die Stückzahlverteilung bei der Herstellung von mehreren Produkten.
Neben diophantischen Gleichungen gibt es noch diophantische Ungleichungen
, die in der
ganzzahligen linearen Optimierung Anwendung finden, und diophantische Approximationen
,
die in der Theorie der Kettenbrüche eine Rolle spielen oder zumindest mit dieser verbunden sind.
Diophantische Gleichungen
Hintergründe
Diophantische Gleichungen sind algebraische Gleichungen, für die nur ganzzahlige Lösungen gesucht werden. Oft, aber nicht immer, sind auch die Koeffizienten der Gleichung ganzzahlig. Meistens sind diophantische Gleichungen unterbestimmte Gleichungssysteme mit mehr Variablen als Gleichungen. Üblich ist eine Gleichung mit mindestens zwei Variablen. Über den reellen oder komplexen Zahlen beschreiben sie algebraische Kurven (oder andere geometrische Formen), deren Geometrie mit der Frage der Existenz und Konstruktion von ganzzahligen Lösungen eng zusammenhängt. Das wird in der „arithmetischen Geometrie“ behandelt, einer Überschneidung von algebraischer Geometrie und Zahlentheorie. Das wichtigste Beispiel sind elliptische Kurven, deren verborgene Gruppenstruktur (Torus-Geometrie der zugehörigen Riemannschen Fläche) sich auch auf die ganzzahligen Punkte überträgt.
Diophantische Gleichungen sind sehr beliebt als Knobelaufgaben oder als Aufgaben für Mathematikolympiaden, da es keinen generischen Lösungsweg gibt und die Lösung oft erhebliche Kreativität erfordert. Gleichzeitig sieht man aber diophantischen Gleichungen im Allgemeinen nicht an, ob sie mit „elementaren“ Methoden lösbar sind oder ob dahinter eine tiefliegende Theorie steckt, die – wie bei der Großen Fermatschen Vermutung – jahrhundertelang eine Lösung unmöglich machten.
Beispiele
- Die lineare Gleichung
mit
.
- Durch Probieren erhält man als eine Lösung
das Paar
.
- Weiterhin gilt
, d. h., man kann
um
verringern und kann das durch Erhöhen von
um
exakt kompensieren. Dadurch kommt man zu weiteren Lösungen wie
und
.
- Die lineare Gleichung
mit
.
- Obwohl mit drei Variablen und nur einer Gleichung deutlich unterbestimmt, gibt es als sogar eindeutige Lösung
das Tripel
.
- Es stellt eine klassische kaufmännische Aufgabe dar:
- Ein Grieche hat 140 Drachmen, ein Schwein kostet 25 Drachmen, ein Schaf 19 Drachmen und eine Ziege 12 Drachmen. Das Geld muss aufgebraucht werden, was kann man unter dieser Maßgabe überhaupt kaufen?
- Darf Geld übrigbleiben, handelt es sich um eine diophantische Ungleichung.
- Die quadratische Gleichung
mit
.
- Die 8 Lösungen sind
und
und sind die Punkte eines Kreises mit dem Radius
und dem Mittelpunkt
, die gerade auf den ganzzahligen Gitterpunkten liegen. Die Lösungsmenge der algebraischen Gleichung ist der gesamte Kreisrand.
- Die quadratische Gleichung
hat als Lösungen
die unendlich vielen Zahlenpaare
; allgemein:
mit
.
- Die Gleichung 6. Grades
hat als Lösung
das Tripel
,
hat keine Lösung und
hat die vier Lösungen
, für
gibt es sogar 8 Lösungen.
- Die lineare Gleichung
besitzt keine Lösung, weil 4 nicht durch 3 teilbar ist und es daher keine ganze Zahl gibt, deren Dreifaches 4 ergibt.
ist keine diophantische Gleichung, da die verwendeten Funktionen
und
keine Potenzfunktionen darstellen (sondern Exponential und Fakultät). In der Literatur bezeichnet man allerdings solche Gleichungen auch als diophantische Gleichungen.
Weiteres
- Man kann diophantische Gleichungen für die Gaußschen Zahlen verallgemeinern. Für lineare Gleichungen sind die gleichen Lösungsansätze wie für ganze Zahlen nutzbar, da der euklidische Algorithmus für Gaußsche Zahlen erweiterbar ist. Entsprechend kann man diophantische Gleichungen für andere algebraische Zahlkörper betrachten. Dort wird dann nach einer Lösung im Ring der ganzen Zahlen des Zahlkörpers gesucht.[1]
- Eine diophantische Gleichung ist ein Spezialfall eines diophantischen Gleichungssystems.
- Beispiel für ein diophantisches Gleichungssystem ist
- mit
. Lösungen
haben die Form
.
Lineare diophantische Gleichung
Diophantische Gleichungen, in denen keine höheren als erste Potenzen der Unbekannten vorkommen, nennt man linear. Für sie gibt es Algorithmen, mit deren Hilfe man stets nach endlich vielen Schritten alle Lösungen findet.
Berühmte diophantische Gleichungen
Berühmte diophantische Gleichungen sind alle nichtlinearen diophantische Gleichungen, die sich (bis auf die Pythagoreischen Tripel) schlecht bis überhaupt nicht generisch lösen lassen, was deren Reiz ausmacht.
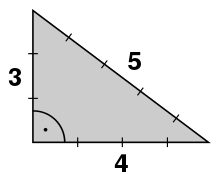
Pythagoreische Tripel a2 + b2 = c2
Die unendlich vielen ganzzahligen Lösungen von
nennt man
pythagoreische Tripel. Man findet sie durch den Ansatz
mit . Neben
ist auch
mit
immer eine Lösung.
Pythagoreische Tripel stellen neben linearen diophantischen Gleichungen eines der ältesten Beispiele dar, zum Beispiel auf babylonischen Keilschrifttafeln aus dem 2. Jahrtausend v.Chr.
Fermats letzter Satz an + bn = cn mit n > 2
Wenn man obige Gleichung zu
verallgemeinert, erhält man eine
diophantische Gleichung vom Grad
. Als Fermats letzten Satz bezeichnet man die von
Pierre de Fermat vor 400 Jahren aufgestellte Behauptung, dass sie für
keine ganzzahlige Lösung besitzt (außer den
trivialen Lösungen, bei denen eine der Zahlen
ist), was erst 1994 von
Andrew Wiles bewiesen wurde. Dahinter steckt die Taniyama-Shimura-Vermutung, die heute vollständig bewiesen ist und nach der alle elliptischen Kurven über den rationalen Zahlen modular sind (eine ganzzahlige Lösung der Fermatgleichungen hätte auf eine Ausnahme geführt).
Den Fall löste schon Fermat mit der von ihm
eingeführten Methode des unendlichen Abstiegs, die auch bei der Frage der Lösbarkeit anderer diophantischer Gleichungen Anwendung fand, aber, wie sich
bald herausstellte, keine universell anwendbare Methode war.
Die unbewiesene abc-Vermutung macht allgemeine Aussagen über Lösungstripel diophantischer Gleichungen der Form
(dabei seien
positive ganze Zahlen und teilerfremd)
und schränkt deren mögliche Lösungen ein, indem sie eine obere Schranke für
in Abhängigkeit von der gemeinsamen multiplikativen
Struktur (Primfaktorzusammensetzung) von
liefert. Die Vermutung nimmt eine zentrale Stellung in der Zahlentheorie und speziell der Theorie diophantischer Gleichungen ein, da viele bekannte Sätze, auch die Lösung der großen Fermatvermutung, daraus folgen.
Eulersche Vermutung für n = 4: a4 + b4 + c4 = d4
Leonhard Euler vermutete (obwohl er
fand), dass es für
keine ganzzahligen Lösung gibt. Euler irrte, es fanden sich aber erst 1987, 1988 und 1997 folgende Lösungen:
Für n ≥ 5
Übrigens wurde schon 1966 für
, d. h. für
mit
eine Lösung gefunden. Weitere Lösungen sind:
Für ist keine Lösungen bekannt.
Für und
wurden folgende Lösungen gefunden:
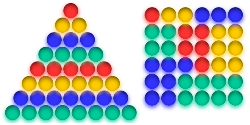
Quadrat-Dreieckszahlen a∕2 · (a+1) = b2
Zahlen, die gleichzeitig Quadrat- wie Dreieckszahlen sind, nennt man Quadrat-Dreieckszahlen. Die unendlich lange Reihe von Lösungen beginnt mit den trivialen Lösungen 0 und 1 und setzt sich fort mit 36, 1225, 41616, 1413721, …
Summe dreier Kubikzahlen a3 + b3 + c3 = n
Für ein gegebenes sind gesucht
, sodass
gilt.
Für existieren keine Lösungen, für
existieren mutmaßlich Lösungen.
Dies ist aber nicht sicher bekannt, genauso wie nicht bekannt ist, wie viele Lösungen es für ein gegebenes
gibt.
Beispiele für jeweils kleinste Lösungen:
Pellsche Gleichung a2 − n b2 = 1
Neben den linearen diophantischen Gleichungen ist die sogenannte Pellsche Gleichung
besonders wichtig, wobei für ein gegebenes natürliches
zunächst das kleinste Wertepaar
zu suchen ist, aus dem sich dann alle anderen
Paare leicht finden lassen. Wenn
eine Quadratzahl
ist, hat diese Gleichung nur die trivialen Lösungen
, ansonsten hat sie unendlich viele Lösungen.
Die Auflösung der Pellschen Gleichung ist gleichbedeutend mit dem Aufsuchen der Einheiten im Ring der algebraisch ganzen Zahlen
des quadratischen Zahlkörpers
, der aus dem
rationalen Zahlkörper
durch
Adjunktion einer Quadratwurzel aus
entsteht.
Summe dreier Quotienten a∕b+c + b∕c+a + c∕a+b = n
Für ein gegebenes sind gesucht
, sodass
gilt.
Die Gleichung hat Lösungen für gerade
, für ungerade
existieren keine Lösungen.
Für ist die kleinste Lösung mit
einfach zu finden. Was aber so harmlos daherkommt, entpuppt sich schon für
als Zahlenmonster. Dafür lautet die kleinste Lösung:
Für findet man die Lösung bei github.com.[2]
Für
hat die kleinste Lösung knapp 400 Millionen Dezimalstellen.[3][4]
Interessant ist, dass man im Gegensatz zu den Kubensummen die Werte ausrechnen kann.
Verallgemeinerte Catalansche Vermutung ap − bq = n
Gesucht sind zwei beliebige ganzzahlige Potenzen, die sich um n voneinander unterscheiden. Für
existiert genau eine Lösung
(
),
was 1844 von Eugène Charles Catalan explizit vermutet wurde und 2002 von
Preda Mihăilescu bewiesen wurde.
Weitere bekannte diophantische Gleichungen
- Erdős-Moser-Gleichung
- Erdős-Straus-Vermutung
- Fermat-Catalan-Vermutung
- Pythagoreisches Quadrupel
- Ramanujan-Nagell-Gleichung
- Rinderproblem des Archimedes
- Taxicab-Zahl
- Waringsches Problem
Einige allgemeine Lösungsmethoden und Endlichkeitssätze für Klassen diophantischer Gleichungen
Axel Thue zeigte 1908,[5] dass die Gleichung
mit einer irreduziblen Form
vom Grad größer oder gleich 3 in zwei
Variablen[6] und einer ganzen Zahl
nur endlich viele Lösungen hat (solche Gleichungen werden
Thue-Gleichungen genannt). Das baute auf seinen Abschätzungen algebraischer Zahlen durch rationale auf (solche Untersuchungen werden diophantische Approximationen genannt) und ist nicht effektiv (das heißt, man erhält daraus kein Lösungsverfahren). Für den Grad 2 gilt der Satz nicht, das zeigt schon die Pellsche Gleichung
mit unendlich vielen Lösungen.
Alan Baker[7] gab 1968 eine effektive obere Grenze für die Lösungen von Thue-Gleichungen mit seiner Methode der linearen Formen in Logarithmen algebraischer Zahlen, ein effizienter Algorithmus zu ihrer Lösung wurde 1989 durch De Weger und Tzanakis angegeben.[8]
1929 bewies Carl Ludwig Siegel, dass für Gleichungen, die algebraische Kurven vom topologischen Geschlecht
beschreiben, nur endlich viele ganzzahlige Lösungen
existieren.[9][10] Auch dieser Beweis war nicht-effektiv und benutzte diophantische Approximationen. Betrachtet
man statt der ganzen Zahlen den Körper der rationalen Zahlen und Kurven des Geschlechts
, entspricht der Satz von Siegel der
Vermutung von Mordell.
1938[11] fand Thoralf Skolem eine ziemlich
allgemeine Lösungsmethode für diophantische Gleichungen der Form
mit einem irreduziblen Polynom
, das in einer Erweiterung des Körpers der rationalen Zahlen in
Faktoren zerfällt und eine weitere Zusatzbedingung erfüllt.
Darunter fällt auch Thues Gleichung für den Fall, dass nicht alle Wurzeln von
reell sind. Skolems Methode beruht
auf p-adischer Analysis (lokale Methode) und nicht auf diophantischen Approximationen wie Thues Methode.
Bei manchen Klassen diophantischer Gleichungen kann auf die Lösbarkeit in rationalen Zahlen aus der Lösbarkeit aus deren Vervollständigungen, den reellen und p-adischen Zahlen, geschlossen werden – allgemein vom lokalen Fall auf den globalen Fall, weshalb dies auch Lokal-Global-Prinzip genannt wird (Helmut Hasse). Das ist aber nicht bei allen diophantischen Gleichungen so.
Hilberts zehntes Problem
Im Jahr 1900 stellte David Hilbert das Problem der Entscheidbarkeit der Lösbarkeit einer diophantischen Gleichung als zehntes Problem seiner berühmten Liste von 23 mathematischen Problemen vor. 1970 bewies Juri Wladimirowitsch Matijassewitsch, dass die Lösbarkeit diophantischer Gleichungen unentscheidbar ist, es also keinen allgemeinen Algorithmus geben kann, der zu einer beliebigen diophantischen Gleichung feststellt, ob sie lösbar oder unlösbar ist. Wichtige Vorarbeiten dazu leisteten Martin Davis, Hilary Putnam und Julia Robinson. Von Davis (1953) stammt die Formulierung als Problem über diophantische Mengen und die Vermutung, dass diese identisch mit den rekursiv aufzählbaren Mengen sind, deren Beweis das 10. Hilbertproblem löste.[12]
Eine diophantische Menge ist eine Menge von
-Tupeln positiver ganzer Zahlen[13]
, die eine Polynomgleichung
erfüllen mit den ebenfalls positiven ganzzahligen Parametern
:
Zum Beispiel bilden die zusammengesetzten Zahlen eine diophantische Menge (das Polynom ist dann
mit den Parametern
), ebenfalls die positiven geraden Zahlen (Polynom
).
Man kann zur Definition auch Systeme von Polynomgleichungen
verwenden, denn diese lassen sich über
auf den Fall einer einzigen Gleichung zurückführen.
Entsprechend sind diophantische Funktionen
durch die diophantischen Mengen
gegeben. Putnam zeigte 1960,
dass jede diophantische Menge natürlicher Zahlen sich als Wertemenge in den natürlichen Zahlen eines ganzzahligen Polynoms darstellen lässt.[14]
Es ist manchmal schwierig zu zeigen, dass eine Menge diophantisch ist. Dies gilt zum Beispiel im Gegensatz zu den zusammengesetzten Zahlen für die Menge der Primzahlen. Denn das Komplement einer diophantischen Menge muss
nach Martin Davis nicht diophantisch sein. Julia Robinson scheiterte zunächst daran zu zeigen, dass
diophantisch ist. Sie zeigte aber,
dass dies folgen würde, wenn man eine diophantische Menge mit exponentiellem Wachstum finden könnte, das heißt solche Mengen, in deren definierender Gleichung eine der Variablen als Exponent auftaucht. Genauer bedeutet dies,
dass gilt (Hypothese von Julia Robinson):
Es gibt eine diophantische Menge , sodass gilt:
- Aus
folgt
.
- Für beliebiges positives
gibt es
mit
.
Diophantische Mengen sind per definitionem rekursiv aufzählbar (es gibt einen Algorithmus, der bei Input aus dieser Menge stoppt).
Zusammen mit Davis und Putnam zeigte Robinson,[15] dass die rekursiv aufzählbaren Mengen genau die exponentiellen diophantischen Mengen sind und der Satz
- „Jede rekursiv aufzählbare Menge ist diophantisch“
folgen würde, wenn man die Existenz einer exponentiell wachsenden diophantischen Menge beweisen könnte (für die die Hypothese von Julia Robinson zutrifft). Das gelang 1970 Matijassewitsch mit Hilfe von Fibonacci-Zahlen, einer exponentiell wachsenden Folge natürlicher Zahlen. Sein Beispiel bestand aus zehn polynomialen Gleichungen mit 15 Unbekannten.[16]
Da es nach der Berechenbarkeitstheorie rekursiv aufzählbare Mengen gibt, die nicht entscheidbar sind (nach einem Argument basierend auf Cantor-Diagonalisierung wie beim Halteproblem), folgt, dass Hilberts zehntes Problem nicht lösbar ist.
Da die Primzahlen rekursiv aufzählbar sind, folgt außerdem, dass es eine diophantische Gleichung gibt, deren Lösung aus allen Primzahlen und nur aus diesen besteht.
Seit Thoralf Skolem war bekannt, dass sich alle diophantischen Gleichungen auf solche vierten oder kleineren Grades zurückführen lassen. Matijassewitsch gelang es außerdem zu zeigen, dass für die Darstellung diophantischer Mengen Polynome in neun und weniger Unbekannten ausreichen.
In Verbindung mit Gödels Unvollständigkeitsresultaten folgt auch, dass es in jedem Axiomensystem der Arithmetik diophantische Gleichungen gibt, die keine Lösung haben, was sich aber nicht innerhalb des Axiomensystems beweisen lässt.[17]
Literatur
- Louis Mordell: Diophantine Equations. Academic Press, 1969.
- G. H. Hardy, E. M. Wright: An Introduction to the Theory of Numbers. 5th ed., Clarendon Press, Oxford, England 1979.
- André Weil: Zahlentheorie – ein Gang durch die Geschichte von Hammurabi zu Legendre. Birkhäuser 1992.
- Isabella Grigorjewna Baschmakowa: Diophant und diophantische Gleichungen. Birkhäuser, Basel 1974.
Zu Hilberts zehntem Problem („Gibt es ein Verfahren festzustellen, ob eine diophantische Gleichung überhaupt Lösungen besitzt“):
- Juri W. Matijassewitsch: Hilbert’s Tenth Problem. Foundations of Computing Series. MIT Press, Cambridge MA u. a. 1993, ISBN 0-262-13295-8.
- Martin Davis, Reuben Hersh: Hilbert’s tenth problem. Scientific American, Band 229, November 1973.
- Martin Davis: Hilbert’s tenth problem is unsolvable. American Mathematical Monthly, Band 80, 1973, S. 233–269.
- Martin Davis, Yuri Matiyasevich, Julia Robinson: Hilbert’s tenth problem, Diophantine equations, positive aspects of a negative solution. In: F. Browder: Mathematical developments arising from Hilbert’s problems. AMS, Teil 2, 1976, S. 323–378.
- Alexandra Shlapentokh: Hilbert’s tenth problem: Diophantine classes and extensions to global fields. Cambridge UP, 2006.
Weblinks
- Eric W. Weisstein:
 Diophantine Equation. In: MathWorld (englisch).
Diophantine Equation. In: MathWorld (englisch). - Christian Spannagel:
 Diophantische Gleichung. Vorlesungsreihe, 2012.
Diophantische Gleichung. Vorlesungsreihe, 2012.
Einzelnachweise und Anmerkungen
- ↑ Zum Beispiel Peck: Diophantine equations in algebraic number fields. American Journal of Mathematics, Band 71, 1949, S. 387–402,
 Jstor, erste Seite.
Jstor, erste Seite.
- ↑
 Lösung für n=16
Lösung für n=16
- ↑ Andrew Bremner, Allan Macleod:
 An unusual cubic representation problem. (PDF; 772 kB). In: ami.uni-eszterhazy.hu. 2014.
An unusual cubic representation problem. (PDF; 772 kB). In: ami.uni-eszterhazy.hu. 2014.
- ↑
 How do you find the positive integer solutions to a/(b+c) + b/(a+c) + c/(a+b) = n. In: quora.com.
How do you find the positive integer solutions to a/(b+c) + b/(a+c) + c/(a+b) = n. In: quora.com.
- ↑ A. Thue: Bemerkungen über gewisse Näherungsbrüche algebraischer Zahlen. Vid.-Selsk., Math.-Naturwiss. Klasse, Nr. 3, Oslo 1908.
- ↑ Anders ausgedrückt:
hat mindestens drei verschiedene Wurzeln.
- ↑ A. Baker: Contributions to the Theory of Diophantine Equations. I. On the Representation of Integers by Binary Forms. Phil. Transactions Royal Society, Band 263, 1968, S. 173–191.
- ↑ N. Tzanakis, B. M. M. De Weger: On the practical solution of the Thue equation. J. of Number Theory, Band 31, 1989, S. 99–132.
- ↑ C. L. Siegel: Über einige Anwendungen diophantischer Approximationen. Sitzungsberichte der Preußischen Akademie der Wissenschaften, Math.-Phys. Klasse, 1929, Nr. 1.
- ↑ Ein Beweis findet sich in:
J.-P. Serre: Lectures on the Mordell-Weil Theorem. Vieweg, 1998.
Einen Beweis mit dem Subspace-Theorem von Wolfgang Schmidt nach Umberto Zannier und P. Corvaja findet man in:
E. Bombieri, W. Gubler: Heights in Diophantine Geometry. Cambridge UP, 2006. - ↑ Th. Skolem: Diophantische Gleichungen. Ergebnisse der Mathematik und ihrer Grenzgebiete. Springer, Berlin 1938, dargestellt in:
Z. I. Borevich, I. R. Shafarevich: Zahlentheorie. Birkhäuser, 1966.
L. Mordell: Diophantine Equations. 1969, Kapitel 23. - ↑ M. Davis: Arithmetical problems and recursively enumerable predicates. J. Symb. Logic, Band 18, 1953, S. 33–41.
- ↑ Es lässt sich ohne Beschränkung der Allgemeinheit zeigen, dass man statt ganzer Zahlen nur natürliche Zahlen zu betrachten braucht.
- ↑ H. Putnam: An unsolvable problem in number theory. J. Symb. Logic, Band 25, 1960, S. 220–232.
- ↑ M. Davis, H. Putnam, J. Robinson: The decision problem for exponential diophantine equations. Annals of Mathematics, Band 74, 1961, S. 425–436.
- ↑ Explizit angegeben zum Beispiel in Davis: Hilbert’s tenth problem. Scientific American, November 1973, S. 91.
- ↑ Davis: Hilbert’s tenth problem. Scientific American, November 1973, S. 91.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.01. 2026