Kreiszahl

Der griechische Kleinbuchstabe Pi ist das Symbol der Kreiszahl.

Ein Kreis mit dem Durchmesser 1 hat den Umfang $\pi$ .

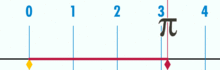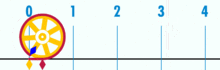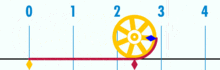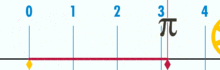
Die Kreiszahl $\pi$ (Pi), auch Ludolphsche Zahl, Ludolfsche Zahl oder Archimedes-Konstante, ist eine mathematische Konstante, die als Verhältnis des Umfangs eines Kreises zu seinem Durchmesser definiert ist. Dieses Verhältnis ist unabhängig von der Größe des Kreises. $\pi$ ist eine transzendente und somit auch irrationale Zahl. Die Dezimalbruchentwicklung der Kreiszahl beginnt mit $\pi =3{,}1415926\ldots ,$ wobei bei praktischen Berechnungen vielfach von $\pi$ lediglich drei signifikante Stellen verwendet werden: $\pi \approx 3{,}14$ .^{[A
1]}

Die Kreiszahl tritt nicht nur in der Geometrie auf, sondern hat auch in anderen mathematischen Teilgebieten und Theorien Bedeutung. Beispielsweise lässt sich durch sie die Lösung des klassischen Basler Problems mit der Theorie der Fourierreihen verknüpfen.

Geschichte der Bezeichnung

Die Kreiszahl und manche ihrer Eigenschaften waren bereits in der Antike bekannt.

Die Bezeichnung mit dem griechischen Buchstaben Pi ( $\pi$ ) (nach dem Anfangsbuchstaben des griechischen Wortes περιφέρεια – zu lateinisch peripheria, „Randbereich“ oder περίμετρος – perimetros, „Umfang“) wurde erstmals von William Oughtred in seiner 1647 veröffentlichten Schrift Theorematum in libris Archimedis de Sphæra & Cylyndro Declaratio verwendet. Darin drückte er mit $\tfrac{\pi}{\delta}$ das Verhältnis von halbem Kreisumfang (semiperipheria) zu Halbmesser (semidiameter) aus, d.h. $\tfrac{\pi}{\delta}= 3{,}1415\ldots$

Dieselben Bezeichnungen benutzte um 1664 auch der englische Mathematiker Isaac Barrow.

David Gregory nahm $\tfrac{\pi}{\rho}$ (1697) für das Verhältnis von Umfang zu Radius.

59 Jahre später als Oughtred, nämlich im Jahr 1706, setzte der walisische Mathematiker William Jones> in seiner Synopsis Palmariorum Matheseos als Erster den griechischen Kleinbuchstaben $\pi$ ein, um das Verhältnis von Umfang zu Durchmesser auszudrücken.

Erst im 18. Jahrhundert wurde $\pi$ durch Leonhard Euler populär. Er verwendete 1737 erstmals $\pi$ für die Kreiszahl, nachdem er zuvor verwendet hatte. Seitdem ist aufgrund der Bedeutung Eulers diese Bezeichnung allgemein üblich.

Definition

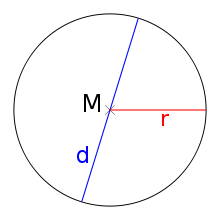
Kreis mit eingezeichnetem Mittelpunkt

Radius und Durchmesser

Es existieren mehrere gleichwertige Ansätze, die Kreiszahl $\pi$ zu definieren.

Die erste (klassische!) Definition in der Geometrie ist die, wonach die Kreiszahl eine Verhältniszahl ist, die numerisch dem aus dem Umfang eines Kreises und dem zugehörigen Durchmesser gebildeten Quotienten $\pi ={\tfrac {U}{d}}$ entspricht. Der zweite Ansatz der Geometrie ist damit verwandt und besteht darin, unter der Kreiszahl den Quotienten $\pi ={\tfrac {A}{r^{2}}}$ zu verstehen, der aus dem Flächeninhalt eines Kreises und dem Flächeninhalt eines über einem Halbmesser (der Länge ) errichteten Quadrates gebildet wird. (Diese Halbmesserlänge bezeichnet man als Kreisradius.) Man fasst diese zweite Definition in den Merksatz, dass sich eine Kreisfläche zur umgebenden Quadratfläche wie $\pi :4$ verhält.

In der Analysis geht man (nach Edmund Landau) oft so vor, zunächst die reelle Kosinusfunktion $\cos(x)$ über ihre Taylorreihe zu definieren und dann die Kreiszahl als das Doppelte der kleinsten positiven Nullstelle des Kosinus festzulegen. Weitere analytische Ansätze gehen auf John Wallis und Leonhard Euler zurück.

Eigenschaften

Irrationalität und Transzendenz

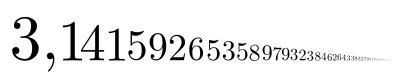
Die Kreiszahl $\pi$ ist transzendent und hat damit unendlich viele Nachkommastellen, die kein sich wiederholendes Muster zeigen.

Die Zahl $\pi$ ist eine irrationale Zahl, also eine reelle, aber keine rationale Zahl. Das bedeutet, dass sie nicht als Verhältnis zweier ganzer Zahlen $p, q \in \mathbb{Z}$ , also nicht als Bruch ${\tfrac {p}{q}}$ , dargestellt werden kann. Das wurde 1761 (oder 1767) von Johann Heinrich Lambert bewiesen.^{[A
2]}

Tatsächlich ist die Zahl $\pi$ sogar transzendent, was bedeutet, dass es kein Polynom mit rationalen Koeffizienten gibt, das $\pi$ als eine Nullstelle hat. Das wurde erstmals von Ferdinand von Lindemann 1882 bewiesen. Als Konsequenz ergibt sich daraus, dass es unmöglich ist, $\pi$ nur mit ganzen Zahlen oder Brüchen und Wurzeln auszudrücken, und dass die exakte Quadratur des Kreises mit Zirkel und Lineal nicht möglich ist.

Die ersten 100 Nachkommastellen

Da $\pi$ eine irrationale Zahl ist, lässt sich ihre Darstellung in keinem Stellenwertsystem vollständig angeben: Die Darstellung ist stets unendlich lang und nicht periodisch. Bei den ersten 100 Nachkommastellen in der Dezimalbruchentwicklung

$\pi =3{,}141\;592\;653\;589\;793\;238\;462\;643\;383\;279\;502\;884\;197\;169\;399\;375\;105\;820\;974\;944\;592\;307\;816\;406\;286\;208\;998\;628\;034\;825\;342\;117\;067\;9\ldots$

ist keine Regelmäßigkeit ersichtlich. Auch weitere Nachkommastellen genügen statistischen Tests auf Zufälligkeit. Siehe auch den Abschnitt zur Frage der Normalität.

Kettenbruchentwicklung

Eine alternative Möglichkeit, reelle Zahlen darzustellen, ist die Kettenbruchentwicklung. Da $\pi$ irrational ist, ist diese Darstellung unendlich lang. Der reguläre Kettenbruch^{[A
3]} der Kreiszahl beginnt so:

$\pi =3+{\frac {1}{7+{\frac {1}{15+{\frac {1}{1+{\frac {1}{292+{\frac {1}{1+{\frac {1}{1+\ddots }}}}}}}}}}}}$

Eine mit der regulären Kettenbruchentwicklung verwandte Entwicklung von $\pi$ ist diejenige als negativ-regelmäßiger Kettenbruch^{[A
4]} (Folge A280135 in OEIS):

$\pi =4-{\frac {1}{2-{\frac {1}{2-{\frac {1}{2-{\frac {1}{2-{\frac {1}{2-{\frac {1}{2-{\frac {1}{17-{\frac {1}{294-\ddots }}}}}}}}}}}}}}}}$

Anders als bei der Eulerschen Zahl konnten bislang bei der regulären Kettenbruchdarstellung von $\pi$ keine Muster oder Gesetzmäßigkeiten festgestellt werden.

Jedoch gibt es nicht-reguläre Kettenbruchdarstellungen von $\pi$ , bei denen einfache Gesetzmäßigkeiten erkennbar sind:

$\pi =3+{\frac {1^{2}}{\scriptstyle 6+{\frac {3^{2}}{6+{\frac {5^{2}}{6+{\frac {7^{2}}{6+{\frac {9^{2}}{6+{\frac {11^{2}}{6+\ddots }}}}}}}}}}}}={\frac {4}{1+{\frac {1^{2}}{2+{\frac {3^{2}}{2+{\frac {5^{2}}{2+{\frac {7^{2}}{2+{\frac {9^{2}}{2+\ddots }}}}}}}}}}}}={\frac {4}{\scriptstyle 1+{\frac {1^{2}}{3+{\frac {2^{2}}{5+{\frac {3^{2}}{7+{\frac {4^{2}}{9+{\frac {5^{2}}{11+\ddots }}}}}}}}}}}}$

Näherungsbrüche der Kreiszahl

Aus ihrer regulären Kettenbruchdarstellung ergeben sich als beste Näherungsbrüche der Kreiszahl (Zähler Folge A002485 in OEIS bzw. Nenner Folge A002486 in OEIS) die folgenden:

Schritt	Kettenbruch	Näherungsbruch	Dezimaldarstellung (falsche Ziffern in rot)	Absoluter Fehler bei der Umfangsberechnung eines Kreises von 1000 km Durchmesser
${\frac {p_{0}}{q_{0}}}$	$[3]$	${\frac {3}{1}}$	$3{,}{\color {red}0}$	− 141,59 km
${\frac {p_{1}}{q_{1}}}$	$[3;7]$	${\frac {22}{7}}$	$3{,}14{\color {red}2\;85\;\ldots }$	+ 1,26 km
${\frac {p_{2}}{q_{2}}}$	$[3;7,15]$	${\frac {333}{106}}$	$3{,}141\;5{\color {red}09\;4\ldots }$	− 83,22 m
${\frac {p_{3}}{q_{3}}}$	$[3;7,15,1]$	$\frac{355}{113}$	$3{,}141\;592\;{\color {red}920\;\ldots }$	+ 26,68 cm
${\frac {p_{4}}{q_{4}}}$	$[3;7,15,1,292]$	${\frac {103993}{33102}}$	$3{,}141\;592\;653\;{\color {red}011\;\ldots }$	− 0,58 mm
${\frac {p_{5}}{q_{5}}}$	$[3;7,15,1,292,1]$	${\frac {104348}{33215}}$	$3{,}141\;592\;653\;{\color {red}921\;\ldots }$	+ 0,33 mm
$\vdots$
${\frac {p_{10}}{q_{10}}}$	$[3;7,15,1,292,1,1,1,2,1,3]$	${\frac {4272943}{1360120}}$	$3{,}141\;592\;653\;589\;{\color {red}389\;\ldots }$	− 0,4 µm (Wellenlänge blauen Lichts)
$\vdots$
${\frac {p_{20}}{q_{20}}}$	$[3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,2,2,2,1]$	${\frac {21053343141}{6701487259}}$	$3{,}141\;592\;653\;589\;793\;238\;462\;{\color {red}381\;\ldots }$	− 2,6·10⁻¹⁶ m (kleiner als ein Proton)

Der absolute Fehler in der Praxis wird dabei schnell vernachlässigbar: Mit der 20. Näherung $\left({\tfrac {p_{20}}{q_{20}}}\right)$ stimmen 21 Nachkommastellen mit denen der Kreiszahl $\pi$ überein. Mit diesem Näherungsbruch wäre erst der Umfang eines Kreises von etwa 3,8 Billiarden km Durchmesser (das entspricht der Entfernung zum Polarstern) um einen Millimeter falsch (hier: zu kurz) berechnet.

Sphärische Geometrie

→ Hauptartikel: Sphärische Geometrie

In der Kugelgeometrie ist der Begriff Kreiszahl nicht gebräuchlich, da das Verhältnis von Umfang zu Durchmesser in diesem Fall nicht mehr für alle Kreise gleich, sondern von deren Größe abhängig ist. Für einen Kreis mit einem sehr viel kleineren Durchmesser als dem der Kugel, auf deren Oberfläche er „gezeichnet“ wird (etwa ein Kreis mit 1 m Durchmesser auf der kugeligen Erdoberfläche), ist die Krümmung der Kugelfläche gegenüber der euklidischen Kreisebene meist vernachlässigbar klein, bei größeren Kreisen oder hoher Präzisionsanforderung muss sie berücksichtigt werden.

Normalität

Eine zurzeit besonders aktuelle mathematische Frage bezüglich $\pi$ ist, ob sie eine normale Zahl ist, das heißt, ob sie zum Beispiel in einer binären (oder jeder anderen n-ären) Zahlendarstellung jede mögliche endliche Binär- bzw. sonstige Zifferngruppe gleichermaßen enthält – so wie es die Statistik erwarten ließe, wenn man eine Zahl vollkommen nach dem Zufall erzeugte.

In letzter Konsequenz würde das beispielsweise bedeuten, dass $\pi$ alle bisher und zukünftig geschriebenen Bücher irgendwo in codierter Binärform enthalten muss (analog zum Infinite-Monkey-Theorem).

Bailey und Crandal zeigten im Jahr 2000 mit der Bailey-Borwein-Plouffe-Formel, dass die Normalität von $\pi$ zur Basis 2 auf eine Vermutung der Chaostheorie reduziert werden kann.

Physiker der Purdue Universität haben im Jahre 2005 die ersten 100 Millionen Dezimalstellen von $\pi$ auf ihre Zufälligkeit hin untersucht und mit kommerziellen Zufallszahlengeneratoren verglichen. Der Forscher Ephraim Fischbach und sein Mitarbeiter Shu-Ju Tu konnten dabei keinerlei verborgene Muster in der Zahl $\pi$ entdecken. Demnach sei nach Ansicht Fischbachs die Zahl $\pi$ tatsächlich eine gute Quelle für Zufälligkeit. Allerdings schnitten einige Zufallszahlengeneratoren noch besser als $\pi$ ab.

Bislang ist nicht einmal bekannt, ob nicht ab einer Stelle beispielsweise nur noch die Ziffern 5 und 6 auftreten.

Geschichte der Berechnung

Die Notwendigkeit, den Umfang eines Kreises aus seinem Durchmesser zu ermitteln oder umgekehrt, stellt sich im ganz praktischen Alltag – man braucht solche Berechnungen zum Beschlagen eines Rades, zum Einzäunen runder Gehege, zum Berechnen der Fläche eines runden Feldes oder des Rauminhalts eines zylindrischen Getreidespeichers. Daher suchten Menschen schon früh nach der exakten Kreiszahl und stellten immer genauere Schätzungen auf.

Schließlich gelang es dem griechischen Mathematiker Archimedes um 250 v.Chr., die Zahl mathematisch einzugrenzen. In der weiteren Geschichte wurden die Versuche zur größtmöglichen Annäherung an $\pi$ phasenweise zu einer regelrechten Rekordjagd, die zuweilen skurrile und auch aufopfernde Züge annahm.

Erste Schätzungen

Berechnungen und Schätzungen in den vorchristlichen Kulturen

Das älteste bekannte Rechenbuch der Welt, das altägyptische Rechenbuch des Ahmes (auch Papyrus Rhind, 16. Jahrhundert v.Chr.), nennt den Wert $\left(\tfrac{16}{9} \right)^2 \approx 3{,}1605.$ Als Näherung für $\pi$ benutzten die Babylonier einfach nur 3 oder auch $3+{\tfrac {1}{8}}=3{,}125.$

Der grobe babylonische Wert 3 findet sich auch in der biblischen Beschreibung des Wasserbeckens, das für den Jerusalemer Tempel geschaffen wurde:

„Dann machte er das Meer. Es wurde aus Bronze gegossen und maß 10 Ellen von einem Rand zum anderen; es war völlig rund und 5 Ellen hoch. Eine Schnur von 30 Ellen konnte es rings umspannen.“

– 1 Kön 7,23

Den Wert 3 nutzte man auch im alten China. In Indien nahm man für die Kreiszahl in den Sulbasutras, den Schnurregeln zur Konstruktion von Altären, den Wert $\left(\tfrac{26}{15} \right)^2 \approx 3{,}0044$ und wenige Jahrhunderte v.Chr. in der Astronomie den Näherungswert ${\sqrt {10}}\approx 3{,}1623.$ Der indische Mathematiker und Astronom Aryabhata gibt 498 n.Chr. das Verhältnis des Kreisumfangs zum Durchmesser mit ${\tfrac {62832}{20000}}=3{,}1416$ an.

Näherungen für den praktischen Alltag

Handwerker benutzten in Zeiten vor Rechenschieber und Taschenrechner die Näherung $\tfrac{22}{7} \approx 3{,}142857$ und berechneten damit vieles im Kopf. Der Fehler gegenüber $\pi$ beträgt etwa 0,04 %. In den meisten Fällen liegt das innerhalb der möglichen Fertigungsgenauigkeit und ist damit völlig ausreichend.

Eine andere oft genutzte Näherung ist der Bruch $\tfrac{355}{113} \approx 3{,}1415929$ , immerhin auf sieben Stellen genau. Allen diesen rationalen Näherungswerten für $\pi$ ist gemeinsam, dass sie partiellen Auswertungen der Kettenbruchentwicklung von $\pi$ entsprechen, z.B.:

$\frac{22}{7} = [3;7],\quad \frac{355}{113} = [3;7,15,1]$

Archimedes von Syrakus

Der Denkansatz: Konstantes Verhältnis bei Flächen- wie Umfangsberechnung

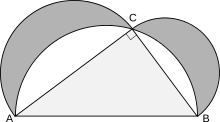
Die Summe der Flächen der grauen Möndchen entspricht der Fläche des rechtwinkligen Dreiecks

Archimedes von Syrakus bewies, dass der Umfang eines Kreises sich zu seinem Durchmesser genauso verhält wie die Fläche des Kreises zum Quadrat des Radius. Das jeweilige Verhältnis ergibt also in beiden Fällen die Kreiszahl. Für Archimedes und noch für viele Mathematiker nach ihm war unklar, ob die Berechnung von $\pi$ nicht doch irgendwann zum Abschluss käme, ob $\pi$ also eine rationale Zahl sei, was die jahrhundertelange Jagd auf die Zahl verständlich werden lässt. Zwar war den griechischen Philosophen mit der Irrationalität von ${\sqrt {2}}$ die Existenz derartiger Zahlen bekannt, dennoch hatte Archimedes keinen Grund, bei einem Kreis von vornherein eine rationale Darstellbarkeit der Flächenberechnung auszuschließen. Denn es gibt durchaus allseitig krummlinig begrenzte Flächen, die sogar von Kreisteilen eingeschlossen sind, die sich als rationale Zahl darstellen lassen wie die Möndchen des Hippokrates.

Erst 1761/1767 konnte Johann Heinrich Lambert die lange vermutete Irrationalität von $\pi$ beweisen.

Annäherung durch Vielecke

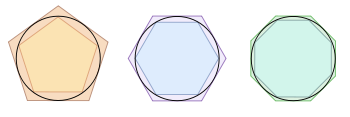
Annäherung an einen Kreis durch Um- und Einbeschreiben von Fünfecken, Sechsecken und Achtecken

Archimedes versuchte wie auch andere Forscher, sich mit regelmäßigen Vielecken dem Kreis anzunähern und auf diese Weise Näherungen für $\pi$ zu gewinnen. Mit umbeschriebenen und einbeschriebenen Vielecken, beginnend bei Sechsecken, durch wiederholtes Verdoppeln der Eckenzahl bis zu 96-Ecken, berechnete er obere und untere Schranken für den Kreisumfang. Er kam zu der Abschätzung, dass das gesuchte Verhältnis etwas kleiner als $3+ \tfrac{10}{70}$ sein müsse, jedoch größer als $3+ \tfrac{10}{71}$ :

$3{,}1408450\approx 3+{\frac {10}{71}}<\pi <3+{\frac {10}{70}}\approx 3{,}1428571$

Laut Heron besaß Archimedes eine noch genauere Abschätzung, die aber falsch überliefert ist:

$3+{\frac {9552}{67441}}<\pi <3+{\frac {10835}{62351}}\qquad (3{,}1416349<\pi <3{,}1737743)$

Wilbur Knorr korrigierte zu:

$3+{\frac {8915}{62991}}<\pi <3+{\frac {9552}{67441}}\qquad (3{,}1415281<\pi <3{,}1416349)$

Genauer und genauer – 3. bis 18. Jahrhundert

Wie in manchen anderen gesellschaftlichen und kulturellen Bereichen gab es auch in der Mathematik in den westlichen Kulturen eine sehr lange Zeit des Stillstandes nach Ende der Antike und während des Mittelalters. Fortschritte in der Annäherung an $\pi$ erzielten in dieser Zeit vor allem chinesische und persische Wissenschaftler.

Im dritten Jahrhundert bestimmte Liu Hui aus dem 192-Eck die Schranken 3,141024 und 3,142704 sowie später aus dem 3072-Eck den Näherungswert 3,1416.

Um 480 berechnete der chinesische Mathematiker und Astronom Zu Chongzhi (429–500) für die Kreiszahl $3{,}1415926<\pi<3{,}1415927$ , also die ersten 7 Dezimalstellen. Er kannte auch den fast genauso guten Näherungsbruch ${\tfrac {355}{113}}$ (das ist der dritte Näherungsbruch der Kettenbruchentwicklung von $\pi$ ), der in Europa erst im 16. Jahrhundert gefunden wurde (Adriaan Metius, deshalb auch Metius-Wert genannt). Im 14. Jahrhundert berechnete Zhao Youqin die Kreiszahl über ein 16384-Eck auf sechs Dezimalstellen genau.

In seinem 1424 abgeschlossenen Werk Abhandlung über den Kreis berechnete der persische Wissenschaftler Dschamschid Masʿud al-Kaschi mit einem 3×2²⁸-Eck $2\pi$ bereits auf 16 Stellen genau.

In Europa gelang es Ludolph van Ceulen 1596, die ersten 35 Dezimalstellen von $\pi$ zu berechnen. Angeblich opferte er 30 Jahre seines Lebens für diese Berechnung. Van Ceulen steuerte allerdings noch keine neuen Gedanken zur Berechnung bei. Er rechnete einfach nach der Methode des Archimedes weiter, aber während Archimedes beim 96-Eck aufhörte, setzte Ludolph die Rechnungen bis zum einbeschriebenen $2^{62}$ -Eck fort. Der Name Ludolphsche Zahl erinnert an seine Leistung.

Der französische Mathematiker François Viète variierte 1593 die Archimedische Exhaustionsmethode, indem er den Flächeninhalt eines Kreises durch eine Folge einbeschriebener $2^{n}$ -Ecke annäherte. Daraus leitete er als Erster eine geschlossene Formel für $\pi$ in Form eines unendlichen Produktes ab:

${\frac {2}{\pi }}={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdot \dots$

John Wallis

Der englische Mathematiker John Wallis entwickelte 1655 das nach ihm benannte wallissche Produkt:

${\frac {\pi }{2}}={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdot \dots$

Wallis zeigte 1655 diese Reihe Lord Brouncker, dem ersten Präsidenten der „Royal Society“, der die Gleichung als Kettenbruch wie folgt darstellte:

$\frac4{\pi}=1+\frac{1^2}{2+\textstyle \frac{ 3^2}{2+\textstyle \frac{5^2}{2+\textstyle \frac{7^2}{2+\textstyle \frac{9^2}{\;\,\ddots}}}}}$

Gottfried Wilhelm Leibniz (Porträt von Christoph Bernhard Francke, um 1700)

Allmählich wurden die Rechnungen komplizierter, Gottfried Wilhelm Leibniz steuerte 1682 folgende Reihendarstellung bei:

${\frac {\pi }{4}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}={\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}\mp \dotsb$

Siehe auch Kreiszahlberechnung nach Leibniz.

Diese war indischen Mathematikern bereits im 15. Jahrhundert bekannt. Leibniz entdeckte sie für die europäische Mathematik neu und bewies die Konvergenz dieser unendlichen Summe. Die obige Reihe ist wegen $\arctan 1 = \tfrac{\pi}4$ auch ein Spezialfall ( $\theta = 1$ ) der Reihenentwicklung des Arkustangens, die der schottische Mathematiker James Gregory in den 1670er Jahren fand:

$\arctan \theta ={\frac {\theta ^{1}}{1}}-{\frac {\theta ^{3}}{3}}+{\frac {\theta ^{5}}{5}}-{\frac {\theta ^{7}}{7}}\pm \dotsb$

Sie war in der folgenden Zeit Grundlage vieler Approximationen von $\pi$ , die alle lineare Konvergenzgeschwindigkeit haben.

Im Jahr 1706 beschrieb William Jones in seinem Werk Synopsis palmariorum matheseos die von ihm entwickelt Reihe, mit der er 100 Nachkommastellen von $\pi$ bestimmte.

William Jones bezeichnete 1706, wie zuvor William Oughtred 1647, die Kreiszahl mit $\pi$

„Let $\alpha =2{\sqrt {3}}.$ […] Then $\alpha -{\frac {1}{3}}{\frac {3\alpha }{9}}+{\frac {1}{5}}{\frac {\alpha }{9}}-{\frac {1}{7}}{\frac {3\alpha }{9^{2}}}+{\frac {1}{9}}{\frac {\alpha }{9^{2}}}-{\frac {1}{11}}{\frac {3\alpha }{9^{3}}}+{\frac {1}{13}}{\frac {\alpha }{9^{3}}},$ & c.“

Ebenfalls im Jahr 1706 berechnete John Machin mit seiner Formel gleichfalls die ersten 100 Dezimalstellen von $\pi$ . Seine Gleichung

${\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}$

lässt sich zusammen mit der taylorschen Reihenentwicklung der Arkustangensfunktion für schnelle Berechnungen verwenden. Diese Formel lässt sich im Reellen über das Additionstheorem des Arkustangens gewinnen, einfacher geht es durch Betrachtung des Argumentes der komplexen Zahl

$(5+\mathrm {i} )^{4}\cdot (239-\mathrm {i} )=114244+114244\;\mathrm {i} =(1+\mathrm {i} )\cdot 114244.$

Im Laufe der Zeit wurden noch mehr Formeln dieser Art gefunden. Ein Beispiel stammt von F. C. W. Størmer (1896):

${\frac {\pi }{4}}=44\,\arctan {\frac {1}{57}}+7\,\arctan {\frac {1}{239}}-12\,\arctan {\frac {1}{682}}+24\,\arctan {\frac {1}{12943}},$

was gleichbedeutend damit ist, dass Real- und Imaginärteil der Gaußschen Zahl

$(57+\mathrm {i} )^{44}\cdot (239+\mathrm {i} )^{7}\cdot (682-\mathrm {i} )^{12}\cdot (12943+\mathrm {i} )^{24}=(1+\mathrm {i} )\cdot n$ mit $n\in \mathbb{Z }$

gleich sind.^{[A
5]}

Leonhard Euler (Pastell von Emanuel Handmann, 1753)

Leonhard Euler führte in seiner im Jahre 1748 erschienenen Introductio in Analysin Infinitorum im ersten Bande $\pi$ bereits auf 148 Stellen genau an. Von Euler entdeckte Formeln (siehe auch Riemannsche ζ-Funktion):

$\zeta (2)={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\dotsb ={\frac {\pi ^{2}}{6}}$

$\zeta (4)={\frac {\pi ^{4}}{90}},\quad \zeta (6)={\frac {\pi ^{6}}{945}},\quad \dotsc$

${\frac {\pi ^{2}}{8}}={\frac {1}{1^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{5^{2}}}+{\frac {1}{7^{2}}}+{\frac {1}{9^{2}}}+\dotsb$

${\frac {\pi -3}{4}}={\frac {1}{2\cdot 3\cdot 4}}-{\frac {1}{4\cdot 5\cdot 6}}+{\frac {1}{6\cdot 7\cdot 8}}\mp \dotsb$

Johann Heinrich Lambert

Lambert: Beyträge zum Gebrauche der Mathematik und deren Anwendung. Band 2, Ausgabe 1, 1792, Seite 156.

Johann Heinrich Lambert publizierte 1770 einen Kettenbruch, der heute meist in der Form

$\frac{4}{\pi}=1+\frac{1^2}{3+\textstyle \frac{2^2}{5+\textstyle \frac{3^2}{7+\textstyle \frac{4^2}{9+\textstyle \frac{5^2} {11+\textstyle \frac{6^2}{\;\,\ddots}}}}}}$

geschrieben wird. Pro Schritt ergeben sich im Mittel etwa 0,76555 Dezimalstellen, was im Vergleich mit anderen Kettenbrüchen relativ hoch ist, sodass sich dieser Kettenbruch besonders gut zur Berechnung von $\pi$ eignet.

Keine der bislang entwickelten Formeln konnte zur effizienten Berechnung von Näherungswerten für $\pi$ dienen, auch die erstaunliche Entdeckung des Inders Srinivasa Ramanujan aus dem Jahr 1914, basierend auf Untersuchungen von elliptischen Funktionen und Modulfunktionen, war dazu noch nicht geeignet:

$\frac{1}{\pi} = \frac{\sqrt{8}}{9801} \cdot\sum_{n=0}^{\infty} \frac{(4 n)! \cdot (1103+26390 n)}{(n!)^{4} \cdot 396^{4 n}}$

Diese Formel liefert schon bei zweimaliger Iteration (bis n=1 ) 15 korrekte Nachkommastellen.

Effizientere Verfahren, deren Implementation allerdings nur bei Verfügbarkeit von Langzahlarithmetik interessant ist, sind Iterationsverfahren mit quadratischer oder noch höherer Konvergenz.

Effiziente Verfahren zur numerischen Berechnung

BBP-Reihen

1995 entdeckte Simon Plouffe zusammen mit Peter Borwein und David Harold Bailey eine neuartige Reihendarstellung für $\pi$ :

$\pi =\sum _{{k=0}}^{{\infty }}{\dfrac 1{16^{k}}}\left({\dfrac 4{8k+1}}-{\dfrac 2{8k+4}}-{\dfrac 1{8k+5}}-{\dfrac 1{8k+6}}\right)$

Diese Reihe (auch Bailey-Borwein-Plouffe-Formel genannt) ermöglicht es, die -te Stelle einer binären, hexadezimalen oder beliebigen Darstellung zu einer Zweierpotenz-Basis von $\pi$ zu berechnen, ohne dass zuvor die n-1 vorherigen Ziffernstellen berechnet werden müssen.

Später wurden für $\pi$ weitere BBP-Reihen gefunden:

${\begin{aligned}\pi &={\frac {1}{2}}\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {8}{8k+2}}+{\frac {4}{8k+3}}+{\frac {4}{8k+4}}-{\frac {1}{8k+7}}\right)\\&={\frac {1}{4}}\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {8}{8k+1}}+{\frac {8}{8k+2}}+{\frac {4}{8k+3}}-{\frac {2}{8k+5}}-{\frac {2}{8k+6}}-{\frac {1}{8k+7}}\right)\\&=\;\;\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{4^{k}}}\left({\frac {2}{4k+1}}+{\frac {2}{4k+2}}+{\frac {1}{4k+3}}\right)\end{aligned}}$

Tröpfelalgorithmus

Eng verwandt mit den Verfahren zur Ziffernextraktion sind Tröpfelalgorithmen, bei denen die Ziffern eine nach der anderen berechnet werden. Den ersten solchen Algorithmus zur Berechnung von $\pi$ fand Stanley Rabinowitz. Seitdem sind weitere Tröpfelalgorithmen zur Berechnung von $\pi$ gefunden worden.

Methode von Gauß, Brent und Salamin

Die Berechnung der Bogenlänge einer Lemniskate über elliptische Integrale und deren Approximation über das Arithmetisch-geometrische Mittel nach Gauß liefert das schnell konvergierende Verfahren von Salamin und Brent zur numerischen Berechnung. Grundlage hierfür ist die folgende zuerst von Gauß vermutete Darstellung von $\pi$ :

${\frac {1}{\pi }}=\mathrm {AGM} (1,{\sqrt {2}})\int _{0}^{1}{\frac {2\mathrm {d} x}{\sqrt {1-x^{4}}}}.$

Letzteres Integral ist auch als lemniskatische Konstante bekannt. Es gilt dann

$\pi ={\frac {4\mathrm {AGM} (1,{\frac {1}{\sqrt {2}}})^{2}}{1-\sum _{j=1}^{\infty }2^{j+1}c_{j}^{2}}}$

wobei sich das arithmetisch-geometrische Mittel über die Iteration

$a_{n}={\frac {a_{n-1}+b_{n-1}}{2}},\qquad b_{n}={\sqrt {a_{n-1}b_{n-1}}}$

mit zwei initialen Argumenten $a_{0},b_{0}>0$ berechnet, und $c_{n}^{2}=a_{n}^{2}-b_{n}^{2}$ gesetzt wird.

Weitere Berechnungsverfahren

Berechnung mittels Flächenformel

In ein Quadrat einbeschriebener Kreis für die Berechnung mittels Flächenformel

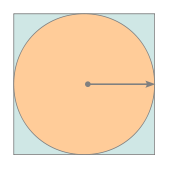
Diese Berechnung nutzt den Zusammenhang aus, dass $\pi$ in der Flächenformel des Kreises enthalten ist, dagegen nicht in der Flächenformel des umschreibenden Quadrats.

Die Formel für den Flächeninhalt des Kreises mit Radius lautet

$A_K = \pi r^2$ ,

der Flächeninhalt des Quadrates mit Seitenlänge errechnet sich als

Für das Verhältnis der Flächeninhalte eines Kreises und seines umschreibenden Quadrats ergibt sich also

${\frac {A_{K}}{A_{Q}}}={\frac {\pi r^{2}}{(2r)^{2}}}={\frac {\pi }{4}}$ .

Damit lässt sich $\pi$ als das Vierfache dieses Verhältnisses schreiben:

$\pi=4\,\frac{A_K}{A_Q}$ .

Programm

Viertelkreis, mit Flächenraster 10×10 angenähert

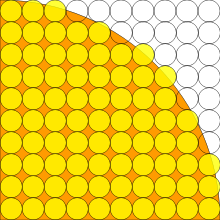
Als Beispiel ist ein Algorithmus angegeben, in dem die Flächenformel demonstriert wird, mit der $\pi$ näherungsweise berechnet werden kann.

Man legt dazu über das Quadrat ein Gitter und berechnet für jeden einzelnen Gitterpunkt, ob er auch im Kreis liegt. Das Verhältnis der Gitterpunkte innerhalb des Kreises zu den Gitterpunkten innerhalb des Quadrats wird mit 4 multipliziert. Die Genauigkeit der damit gewonnenen Näherung von $\pi$ hängt von der Gitterweite ab und wird mittels kontrolliert. Mit r = 10 erhält man z.B. 3,16 und mit r = 100 bereits 3,1428. Für das Ergebnis 3,14159 ist allerdings schon r = 10000 zu setzen, was sich durch den zweidimensionalen Lösungsansatz auf die Zahl der notwendigen Rechenvorgänge in quadratischer Form niederschlägt.

 r = 10000
 kreistreffer = 0
 quadrattreffer = r ^ 2
 for i = 0 to r - 1
   x = i + 0.5
   for j = 0 to r - 1
     y = j + 0.5
     if x ^ 2 + y ^ 2 <= r ^ 2 then
       kreistreffer = kreistreffer + 1
 return 4 * kreistreffer / quadrattreffer

Anmerkung: Das obige Programm ist nicht für die schnellstmögliche Ausführung auf einem realen Computersystem optimiert, sondern aus Gründen der Verständlichkeit so klar wie möglich formuliert worden. Weiterhin ist die Kreisfläche insofern unpräzise bestimmt, als nicht die Koordinaten der Mitte für die jeweiligen Flächeneinheiten benutzt werden, sondern der Flächenrand. Durch die Betrachtung eines Vollkreises, dessen Fläche für die erste und letzte Zeile gegen Null geht, ist die Abweichung für großes marginal.

Die Konstante Pi ist für den Alltagsgebrauch in Computerprogrammen typischerweise bereits vorberechnet vorhanden, üblicherweise ist der zugehörige Wert dabei mit etwas mehr Stellen angegeben, als ihn die leistungsfähigsten Datentypen dieser Computersprache aufnehmen können.

Alternatives Programm

Kreisflächen-Integration

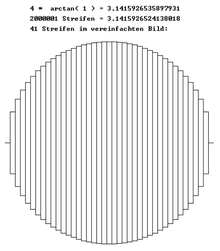
Dieses Programm summiert die Fläche des Kreises aus im Verhältnis zum Radius sehr schmalen Streifen. Es verwendet die Gleichungen
$y = \pm \sqrt{r^2 - x^2}$ und $\pi ={\frac {A_{K}}{r^{2}}}$ sowie $\pi =\int _{-1}^{1}2{\sqrt {1-x^{2}}}\,\mathrm {d} x$ .

n := 1000000 // Halbe Anzahl der Streifen
s := 0       // Summe der Flächeninhalte

for x := -1 to +1 step 1/n:
    // Flächeninhalt des Streifens an der Stelle x hinzuaddieren.
    // Die Höhe des Streifens wird exakt in der Mitte des Streifens gemessen.
    // Die 2 steht für die obere plus die untere Hälfte.
    // Der Faktor 1/n ist die Breite des Streifens.
    s += 2 * sqrt(1 - x*x) * 1/n

pi := s

Die x-Koordinaten der untersuchten Fläche gehen von bis . Da Kreise rund sind und dieser Kreis sein Zentrum auf den Koordinaten $0,0$ hat, liegen die y-Koordinaten ebenfalls im Bereich von bis . Das Programm teilt die zu untersuchende Fläche in 2 Millionen schmale Streifen auf. Jeder dieser Streifen hat dieselbe Breite, nämlich 1/n . Die Oberkante eines jeden Streifens ist jedoch unterschiedlich und ergibt sich aus der obigen Formel zu ${\sqrt {1-x^{2}}}$ , im Code wird das als sqrt(1 - x*x) geschrieben. Die Höhe eines jeden Streifens geht von der Oberkante bis zur Unterkante. Da die beiden Kanten bei Kreisen gleich weit von der Mittellinie entfernt sind, ist die Höhe genau das Doppelte der Kantenlänge, daher die 2 im Code.

Nach dem Durchlaufen der for-Schleife befindet sich in der Variablen s der Flächeninhalt des Kreises mit Radius 1. Um aus dieser Zahl den Wert von Pi zu ermitteln, muss diese Zahl gemäß der Formel $A=\pi \cdot r^{2}$ noch durch $r^{2}$ geteilt werden. In diesem Beispiel ist r=1 , daher ist das im Programmcode weggelassen.

Statistische Bestimmung

Berechnung mit einem Monte-Carlo-Algorithmus

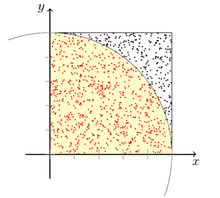
Viertelkreis, dessen Fläche durch die Monte-Carlo-Methode angenähert wird

Eine Methode zur Bestimmung von $\pi$ ist die statistische Methode. Für die Berechnung lässt man zufällige Punkte auf ein Quadrat „regnen“ und berechnet, ob sie innerhalb oder außerhalb eines einbeschriebenen Kreises liegen. Der Anteil der innen liegenden Punkte ist $\approx {\tfrac {\pi }{4}}.$

Diese Methode ist ein Monte-Carlo-Algorithmus; die Genauigkeit der nach einer festen Schrittzahl erreichten Näherung von $\pi$ lässt sich daher nur mit einer Irrtumswahrscheinlichkeit angeben. Durch das Gesetz der großen Zahlen steigt jedoch im Mittel die Genauigkeit mit der Schrittzahl.

Der Algorithmus für diese Bestimmung ist:

function approximiere_pi(tropfenzahl)

    innerhalb := 0   // Zählt die Tropfen innerhalb des Kreises

    // So oft wiederholen, wie es Tropfen gibt:
    for i := 1 to tropfenzahl do

        // Zufälligen Tropfen im Quadrat [0,0] bis (1,1) erzeugen
        x := random(0.0 ..< 1.0)
        y := random(0.0 ..< 1.0)

        // Wenn der Tropfen innerhalb des Kreises liegt ...
        if x * x + y * y <= 1.0
            innerhalb++   // Zähler erhöhen

    return 4.0 * innerhalb / tropfenzahl

Die 4.0 im Code ergibt sich daraus, dass in der Tröpfchensimulation nur die Anzahl für einen Viertelkreis berechnet wurde. Um daraus die (hochgerechnete) Anzahl für einen ganzen Kreis zu bekommen, muss die berechnete Anzahl noch mit 4 multipliziert werden. Da die Zahl Pi das Verhältnis zwischen der Kreisfläche und dem Quadrat des Radius ist, muss die so erhaltene Zahl noch durch das Quadrat des Radius geteilt werden. Der Radius ist in diesem Fall 1, daher kann das Teilen weggelassen werden.

Buffonsches Nadelproblem

Eine weitere auf Wahrscheinlichkeiten beruhende und ungewöhnliche Methode ist das Buffonsche Nadelproblem von Georges-Louis Leclerc de Buffon (1733 vorgetragen, 1777 veröffentlicht). Buffon warf Stöcke über die Schulter auf einen gekachelten Fußboden. Anschließend zählte er, wie oft sie die Fugen trafen. Eine praktikablere Variante beschrieb Jakow Perelman im Buch Unterhaltsame Geometrie. Man nehme eine ca. 2 cm lange Nadel – oder einen anderen Metallstift mit ähnlicher Länge und Durchmesser, am besten ohne Spitze – und zeichne auf ein Blatt Papier eine Reihe dünner paralleler Striche, die um die doppelte Länge der Nadel voneinander entfernt sind. Dann lässt man die Nadel sehr häufig (mehrere hundert- oder tausendmal) aus einer beliebigen aber konstanten Höhe auf das Blatt fallen und notiert, ob die Nadel eine Linie schneidet oder nicht. Es kommt nicht darauf an, wie man das Berühren eines Striches durch ein Nadelende zählt. Die Division der Gesamtzahl der Nadelwürfe durch die Zahl der Fälle, in denen die Nadel eine Linie geschnitten hat, ergibt

${\frac {N}{P}}={\frac {\pi }{2}}{\frac {d}{\ell }}$ ,

wobei $\ell$ die Länge der Nadeln und den Abstand der Linien auf dem Papier bezeichnet. Daraus ergibt sich leicht eine Näherung für $\pi$ . Die Nadel kann dabei auch gebogen oder mehrfach geknickt sein, wobei in diesem Fall auch mehr als ein Schnittpunkt pro Wurf möglich ist und entsprechend mehrfach gezählt werden muss. In der Mitte des 19. Jahrhunderts kam der Schweizer Astronom Rudolf Wolf durch 5000 Nadelwürfe auf einen Wert von $\pi =3{,}1596\pm 0{,}0518$ .

Geometrische Konstruktionen

Aufgrund der Transzendenz von $\pi$ ist es nicht möglich, durch eine Konstruktion mit Zirkel und Lineal eine Strecke mit der exakten Länge von $\pi$ Längenheiten zu erstellen. Es existieren jedoch sowohl eine Reihe von Zirkel-und-Lineal-Konstruktionen, die sehr gute Näherungen liefern, als auch Konstruktionen, die dank eines weiteren Hilfsmittels zusätzlich zu Zirkel und Lineal eine exakte Konstruktion ermöglichen. Als ein solches weiteres Hilfsmittel kommen dabei insbesondere als Quadratizes bezeichnete Kurven zum Einsatz, die mit Hilfe eines speziellen Zeichengeräts oder einer Schablone gezeichnet werden können.

Näherungskonstruktionen

Zur geometrischen Konstruktion der Zahl $\pi$ gibt es die Näherungskonstruktion von Kochański aus dem Jahr 1685, mit der man einen Näherungswert der Kreiszahl mit einem Fehler von weniger als 0,002 Prozent bestimmen kann. Es handelt sich also um eine Näherungskonstruktion für die (exakt nicht mögliche) Quadratur des Kreises.

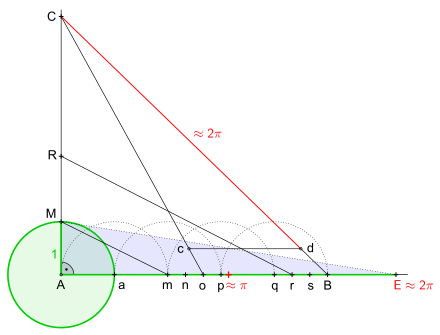
Kreiszahl π, Annäherungskonstruktion nach C. G. Specht, 1828.
Der Flächeninhalt des ergänzten Dreiecks $AEM$ (hellblau) ist nahezu gleich dem des Kreises.

143 Jahre später, nämlich 1828, veröffentlichte C. G. Specht seine Zweite Annäherungs-Construction des Kreis-Umfanges im Journal für die reine und angewandte Mathematik. Für die Annäherung fand er den Wert

$5\cdot {\sqrt {\frac {439}{278}}}=6{,}28318528\ldots$

Halbiert man diesen Wert, ergibt sich eine Dezimalzahl, bei der sieben Nachkommastellen mit denen der Kreiszahl $\pi$ übereinstimmen:

$3{,}141\;592\;6{\color {red}40\;1\ldots }\;\approx \pi$

Bei einem Kreis mit Radius r=1 ist dieser Wert auch gleich dem Flächeninhalt des Dreiecks $AEM$ , mit anderen Worten, der Flächeninhalt des Dreiecks ist nahezu gleich dem des Kreises.

Beachtenswert ist, erst im Jahr 1914, d.h. 86 Jahre später, verbesserte Srinivasa Ramanujan – in seiner zweiten Quadratur des Kreises – die Genauigkeit des nahezu flächengleichen Quadrats um eine auf acht gemeinsame Nachkommastellen mit der Kreiszahl $\pi.$

Eine zeichnerische Darstellung wird in dem oben angeführten Journal nicht erfasst; hierzu die Anmerkung des Herausgebers:

“ *) Es wird dem Leser leicht sein, die Figur nach der Beschreibung zu entwerfen.”

– C. G. Specht: 40. Zweite Annäherungs-Construction des Kreis-Umfanges.

Die nachfolgende Beschreibung der nebenstehenden Konstruktion ist eine Anlehnung an das Original der Konstruktionsbeschreibung.

Zeichne zuerst den Einheitskreis um den Punkt und dann ab eine gerade Linie; dabei ergibt sich . Anschließend wird in eine Senkrechte zur Geraden errichtet; sie erzeugt . Es folgen auf der Geraden ab hintereinander vier Halbkreise mit dem Radius ${\overline {Aa}}$ jeweils um den sich neu ergebenden Schnittpunkt, dabei entstehen die Punkte $m,p,q$ und . Nach der Dreiteilung der Strecken ${\overline {mp}}$ in und sowie ${\overline {qB}}$ in und , wird nun der Punkt mit verbunden. Die dabei entstandene Strecke ${\overline {Mm}}$ auf die Senkrechte ab abgetragen ergibt . Verbinde auch den Punkt mit und übertrage die neue Strecke ${\overline {Rr}}$ ab auf die Senkrechte; es ergibt sich . Es geht weiter mit den Verbindungen der Punkte mit sowie mit . Beim Übertragen der Strecke ${\overline {AB}}$ auf die Strecke ${\overline {Co}}$ ab ergibt sich . Abschließend zeichne ab eine Parallele zur Strecke ${\overline {AB}}$ , die ${\overline {CB}}$ in schneidet. Die somit entstandene Strecke ${\overline {Cd}}$ entspricht annähernd dem Wert $2\pi$ .

Die Annäherung an die Kreiszahl $\pi ={\tfrac {U}{d}}$ kann z.B. auf folgende Art und Weise verdeutlicht werden:

Wäre der Durchmesser eines Kreises $100\;\mathrm {km}$ , würde sein angenäherter Umfang $U=d\pi$ nur um ca. $2{,}7\;\mathrm {mm}$ kürzer als sein theoretischer Wert sein.

Quadratrix des Hippias als zusätzliches Hilfsmittel

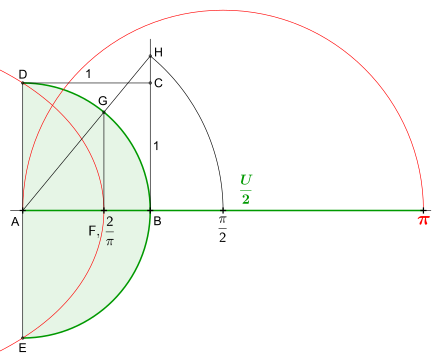
Kreiszahl $\pi$ als exakte Konstruktion mithilfe der Quadratrix, Radius

Die nebenstehende Darstellung zeigt die Kreiszahl $\pi$ als Strecke, erstellt mit Hilfe der Quadratrix des Hippias.

Es beginnt mit einer Geraden ab dem Punkt und einer Senkrechten auf diese Gerade durch . Anschließend wird der Halbkreis mit dem Radius r=1 um gezogen; dabei ergeben sich die Schnittpunkte $B,D$ und . Nun konstruiert man das Quadrat ABCD mit der Seitenlänge 1. Es folgt die Konstruktion der Quadratrix, ohne „Lücke“ auf der X-Achse, mit der Parameterkurve $\gamma \colon (-\pi ,\pi )\rightarrow \mathbb {R} ^{2}$ :

$\gamma (t)={\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}$

mit

${\begin{aligned}x(t)&={\begin{cases}{\frac {2}{\pi }}t\cot(t)\,&,t\in (-\pi ,\pi )\setminus \{0\}\\{\frac {2}{\pi }}\,&,t=0\end{cases}}\\y(t)&={\frac {2}{\pi }}t\end{aligned}}$

Die Quadratrix schneidet nach dem Satz des Dinostratos die Seite ${\overline {AB}}$ ihres zugehörigen Quadrates im Punkt und generiert damit auf der Geraden, nun als Zahlengerade genutzt, den Wert $\tfrac{2}{\pi}$ . Das Errichten der Senkrechten auf die Strecke ${\overline {AB}}$ ab $\tfrac{2}{\pi}$ bis zum Halbkreis ergibt den Schnittpunkt . Nach der Verlängerung der Strecke ${\overline {BC}}$ über hinaus und dem Zeichnen einer geraden Linie ab durch bis zur Verlängerung ergibt sich der Schnittpunkt . Eine Möglichkeit u.a. ist nun, die Länge der Strecke $\overline{AH}$ mit Hilfe des Strahlensatzes zu bestimmen. In der Zeichnung ist ersichtlich, dass $\tfrac{2}{\pi}$ der Strecke ${\overline {AF}}$ entspricht. Infolgedessen sind nach dem ersten Strahlensatz die Verhältnisse der Abschnitte

$|AF|:|AB|=|AG|:|AH|,$

umgeformt und die entsprechenden Werte eingesetzt ergibt sich

$|AH|={\frac {\frac {1}{1}}{\frac {2}{\pi }}}\cdot 1={\frac {\pi }{2}}.$

Nun wird der Kreisbogen mit dem Radius $\overline{AH}$ um bis auf die Zahlengerade gezogen; es entsteht der Schnittpunkt ${\tfrac {\pi }{2}}$ . Der abschließende Thaleskreis über ${\tfrac {\pi }{2}}$ ab dem Punkt ergibt somit exakt die Kreiszahl $\pi$ .

Experimentelle Konstruktion

Kreiszahl $\pi$ als experimentelle Konstruktion:
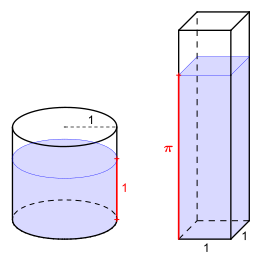
1. Zylinder mit Wasserstand = $1\,\mathrm {[LE]}$
2. Quader mit umgefüllter Wassermenge, Wasserstand = $\pi \,\mathrm {[LE]}$

Die folgende Methode nutzt die in der Kreisfläche „versteckte“ Kreiszahl $\pi$ , um mit Hilfe experimenteller Physik den Wert von $\pi$ als messbare Größe darzustellen.

Ein Zylinder mit dem Radius r=1 und der Gefäßhöhe ${\hat {h}}_{\text{Z}}\approx 1{,}5$ wird bis auf die Höhe $h_{\text{Z}}=1$ mit Wasser gefüllt. Die so bestimmte Wassermenge wird nun vom Zylinder in einen Quader umgefüllt, der eine quadratische Grundfläche mit Seitenlänge a=1 und eine Gefäßhöhe von ${\hat {h}}_{\text{Q}}\approx 4$ aufweist.

Wassermenge im Zylinder $V_{\text{Z}}$ in Volumeneinheiten [VE]:

$V_{\text{Z}}=r^{2}\pi h_{\text{Z}}=1^{3}\cdot \pi =3{,}14159\dotso \,\mathrm {[VE]}$

Wasserstand im Quader $h_{\text{Q}}$ in Längeneinheiten [LE]:

$V_{\text{Q}}=a^{2}h_{\text{Q}}=1^{2}h_{\text{Q}}=V_{\text{Z}}$ , daraus $h_{\text{Q}}$

$h_{\text{Q}}={\frac {1^{3}\pi }{1^{2}}}=\pi =3{,}14159\dotso \,\mathrm {[LE]}$

Das Ergebnis zeigt: Eine Wassermenge, die im Zylinder den Wasserstand 1 [LE] hat, liefert – umgefüllt in den Quader – den Wasserstand $\pi \,\mathrm {[LE]}$ .

Formeln und Anwendungen

Formeln, die π enthalten

Formeln der Geometrie

In der Geometrie treten die Eigenschaften von $\pi$ als Kreiszahl unmittelbar hervor.

Umfang eines Kreises mit Radius : $U = 2 \pi r$
Fläche eines Kreises mit Radius : $A = \pi r^2$
Volumen einer Kugel mit Radius : $V={\frac {4}{3}}\pi r^{3}$
Oberfläche einer Kugel mit Radius : $A_O = 4 \pi r^2$
Volumen eines Zylinders mit Radius und Höhe : $V = r^2 \pi a$
Volumen eines durch die Rotation des Graphen um die -Achse definierten Rotationskörpers mit den Grenzen und : $V = \pi \int_a^b f(x)^2 \mathrm{d}x$

Formeln der Analysis

Carl Friedrich Gauß

Jean Baptiste Joseph Fourier

Im Bereich der Analysis spielt $\pi$ ebenfalls in vielen Zusammenhängen eine Rolle, zum Beispiel bei

der Integraldarstellung $\pi = \int_{-\infty}^\infty \frac{\mathrm{d} x}{1 + x^2} = 2\cdot \int_{-1}^1 \frac{\mathrm{d} x}{1 + x^2}$ , die Karl Weierstraß 1841 nutzte, um $\pi$ zu definieren,
der unendlichen Reihe: $\sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6}$ (Euler, siehe auch Riemannsche Zetafunktion),
der gaußschen Normalverteilung: $\int_{-\infty}^{\infty} e^{-x^2} \mathrm{d}x = \sqrt\pi$ oder in anderer Darstellung: $\int_{\mathbb{R}^2} e^{-|x|^2} \mathrm{d}x = \pi$ ,
der Stirling-Formel als Näherung der Fakultät für große : $n! \approx \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n$ ,
der Fourier-Transformation: $F(\omega )={\mathcal {F}}\{f\}(\omega )={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }f(t)e^{-\mathrm {i} \omega t}\,\mathrm {d} t$ .

Formeln der Funktionentheorie

Wie für alle Teilgebiete der Analysis ist auch für die Funktionentheorie (und darüber hinaus für die gesamte komplexe Analysis) die Kreiszahl von grundlegender Bedeutung. Als herausragende Beispiele sind hier

die Euler-Identität $e^{\mathrm {i} \pi }+1=0$ ^{[A
6]}

zu nennen sowie

die Integralformel von Cauchy $f(z)={\frac {1}{2\pi \mathrm {i} }}\oint _{\gamma }{\frac {f(\zeta )}{\zeta -z}}\mathrm {d} \zeta$ .

Darüber hinaus wird die Bedeutung der Kreiszahl ebenfalls augenfällig in den Formeln zur Partialbruchzerlegung der komplexwertigen trigonometrischen Funktionen, die im Zusammenhang mit dem Satz von Mittag-Leffler stehen. Hier sind vor allem

die Partialbruchzerlegung des Kotangens:

${\begin{aligned}\pi \cot(\pi z)&=\sum _{n={-\infty }}^{+\infty }{\frac {1}{z+n}}\\&={\frac {1}{z}}+\sum _{n=1}^{\infty }\left({\frac {1}{z-n}}+{\frac {1}{z+n}}\right)\\&={\frac {1}{z}}+2z\cdot \sum _{n=1}^{\infty }{\frac {1}{z^{2}-n^{2}}}\\&=z\cdot \sum _{n={-\infty }}^{+\infty }{\frac {1}{z^{2}-n^{2}}}\quad (z\in {\mathbb {C} \setminus \mathbb {Z} })\\\end{aligned}}$

zu erwähnen sowie die daraus – neben weiteren! – zu gewinnenden

Partialbruchzerlegungen zu Sinus und Kosinus:

${\begin{aligned}\left({\frac {\pi }{\sin(\pi z)}}\right)^{2}&=\sum _{n={-\infty }}^{+\infty }{\frac {1}{(z-n)^{2}}}\quad (z\in {\mathbb {C} \setminus \mathbb {Z} })\\\left({\frac {\pi }{\cos(\pi z)}}\right)^{2}&=\sum _{n={-\infty }}^{+\infty }{\frac {1}{(z-{\tfrac {2n-1}{2}})^{2}}}\quad \left(z\in \mathbb {C} \setminus \left\{{\frac {2n-1}{2}}\colon n\in \mathbb {Z} \right\}\right)\\\end{aligned}}$

Die obige Partialbruchreihe zum Sinus liefert dann durch Einsetzen von $z=\frac{1}{2}$ die bekannte Reihendarstellung

${\frac {{\pi }^{2}}{8}}=1+{\frac {1}{9}}+{\frac {1}{25}}+{\frac {1}{49}}+\cdots =\sum _{n=1}^{\infty }{\frac {1}{(2n-1)^{2}}},$

die ihrerseits direkt zu der eulerschen Reihendarstellung

${\frac {{\pi }^{2}}{6}}=1+{\frac {1}{4}}+{\frac {1}{9}}+{\frac {1}{16}}+\cdots =\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}$

führt.

Neben diesen von den Partialbruchreihen herrührenden π-Formeln kennt die Funktionentheorie noch eine große Anzahl weiterer davon, die statt der Darstellung mit unendlichen Reihen eine Darstellung mittels unendlicher Produkte aufweisen. Viele von ihnen gehen auf das Werk von Leonhard Euler zurück (su.).

Formeln der Zahlentheorie

Die relative Häufigkeit, dass zwei zufällig gewählte natürliche Zahlen, die unterhalb einer Schranke liegen, teilerfremd sind, strebt mit $M \rightarrow \infty$ gegen $\frac{6}{\pi^2}$ .

Formeln der Physik

In der Physik spielt $\pi$ neben

der Kreisbewegung: $\omega =2\pi f$ (Winkelgeschwindigkeit gleich $2\pi$ mal Umlauffrequenz)

vor allem bei Wellen eine Rolle, da dort $\pi$ über die Sinus- und Kosinusfunktion eingeht; somit also zum Beispiel

in der Quantenmechanik: $\Delta x \Delta p \ge \frac{h}{4 \pi}$ (Heisenbergsche Unschärferelation),

außerdem

in der Berechnung der Knicklast $F_K=\frac{\pi^2EI}{s^2}$
und bei der Reibung von Partikeln in Flüssigkeiten (Gesetz von Stokes) $F_R=6 \, \pi \, \eta \, r \, v.$

Produktformeln von Leonhard Euler

Wird die Folge der Primzahlen wie üblich mit $\bigl(p_k \bigr)_{k \in \N} = \bigl(2,3,5,7, \dots \bigr)$ bezeichnet, so gilt:

$\begin{align} \frac{{\pi}^2}{6} &= \prod_{k=1}^{\infty} { \frac{{p_k}^2}{{p_k}^2 - 1} } &= \frac{2^2}{2^2 - 1} \cdot \frac{3^2}{3^2 - 1} \cdot \frac{5^2}{5^2 - 1} \cdot \frac{7^2}{7^2 - 1} \cdot \; \dots &= \frac{4}{3} \cdot \frac{9}{8} \cdot \frac{25}{24} \cdot \frac{49}{48} \cdot \; \dots \\ \frac{{\pi}^4}{90} &= \prod_{k=1}^{\infty} { \frac{{p_k}^4}{{p_k}^4 - 1} } &= \frac{2^4}{2^4 - 1} \cdot \frac{3^4}{3^4 - 1} \cdot \frac{5^4}{5^4 - 1} \cdot \frac{7^4}{7^4 - 1} \cdot \; \dots &= \frac{16}{15} \cdot \frac{81}{80} \cdot \frac{625}{624} \cdot \frac{2401}{2400} \cdot \; \dots \\ \frac{{\pi}^8}{9450} &= \prod_{k=1}^{\infty} { \frac{{p_k}^8}{{p_k}^8 - 1} } &= \frac{2^8}{2^8 - 1} \cdot \frac{3^8}{3^8 - 1} \cdot \frac{5^8}{5^8 - 1} \cdot \frac{7^8}{7^8 - 1} \cdot \; \dots &= \frac{256}{255} \cdot \frac{6561}{6560} \cdot \frac{390625}{390624} \cdot \frac{5764801}{5764800} \cdot \; \dots \\ \end{align}$

Es gehen auf Euler auch die folgenden Produktformeln zurück, welche die Kreiszahl mit der komplexen Gammafunktion und dem komplexen Sinus und Kosinus verbinden:

Die erste der drei folgenden Formeln bezeichnet man auch als eulerschen Ergänzungssatz. Bei den beiden anschließenden Produktformeln für Sinus und Kosinus handelt es sich um absolut konvergente Produkte. Beide Produktformeln ergeben sich aus dem Ergänzungssatz, wobei die Produktformel des Kosinus ihrerseits wegen $\cos(z)={\tfrac {\sin(2z)}{2\sin(z)}}$ eine direkte Anwendung der Produktformel des Sinus ist.

${\begin{aligned}\Gamma (z)\cdot \Gamma (1-z)&={\frac {\pi }{\sin(\pi z)}}\quad (z\in \mathbb {C} \setminus \mathbb {Z} )\\\sin(\pi z)&=\pi z\prod _{k=1}^{\infty }\left(1-{\frac {z^{2}}{k^{2}}}\right)\quad (z\in \mathbb {C} )\\\cos(\pi z)&=\prod _{k=1}^{\infty }\left(1-{\frac {4z^{2}}{(2k-1)^{2}}}\right)\quad (z\in \mathbb {C} )\\\end{aligned}}$

Die Produktformel des Sinus führt dann mit $z = \mathrm i$ zu dieser interessanten Beziehung (Folge

A156648 in OEIS):

${\begin{aligned}\prod _{k=1}^{\infty }\left(1+{\frac {1}{k^{2}}}\right)&={\frac {e^{\pi }-e^{-\pi }}{2\pi }}&={\frac {\sinh(\pi )}{\pi }}&\approx 3{,}6760779103749\\\end{aligned}}$

Entwicklung der Nachkommastellen von π

Mathematiker	Jahr	Dezimalstellen	Methode	Rechenzeit
Ägypten, Rechenbuch des Ahmes (Papyrus Rhind)	ca. 16. Jh. v.Chr.	1	Beispiel
Archimedes	ca. 250 v.Chr.	2	96-Eck
Liu Hui	nach 263	5	3072-Eck
Zu Chongzhi	ca. 480	6
Dschamschid Masʿud al-Kaschi	ca. 1424	15	3 · 2²⁸-Eck
Ludolph van Ceulen	1596	20
Ludolph van Ceulen	1610	35	2⁶²-Eck
William Jones John Machin	1706	100	Reihenentwicklungen William Jones: Es sei $\alpha =2{\sqrt {3}},$ dann ist $\pi =\alpha -{\frac {1}{3}}{\frac {3\alpha }{9}}+{\frac {1}{5}}{\frac {\alpha }{9}}-{\frac {1}{7}}{\frac {3\alpha }{9^{2}}}+{\frac {1}{9}}{\frac {\alpha }{9^{2}}}-{\frac {1}{11}}{\frac {3\alpha }{9^{3}}}+{\frac {1}{13}}{\frac {\alpha }{9^{3}}}\ldots$ John Machin: ${\frac {\pi }{2}}={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\dotsm$
Jurij Vega	1794	126
William Shanks	1853	(527)	Reihenentwicklung von $\arctan \tfrac{1}{5}$ und $\arctan \tfrac{1}{239}$ . Berechnung der ersten 707 Dezimalstellen von $\pi$ von Hand. Im Jahr 1945 wurde entdeckt, dass die letzten 180 Stellen falsch waren.
Levi B. Smith, John W. Wrench	1949	1.120
G. Reitwiesner	1949	2.037	mit dem Röhren-Rechner ENIAC	70 h
Nicholson, Jaenel	1954	3.092	Naval Ordnance Research Calculator	0:13 h
George E. Felton	1957	7.480	Pegasus	33 h
F. Genuys	1958	10.000	mit dem Magnetkernspeicher-Rechner IBM 704, per Machin-Formel	10 h
George E. Felton	1958	10.021	Pegasus	33 h
Jean Guilloud	1959	16.167	IBM 704	4:18 h
Daniel Shanks, John W. Wrench	1961	100.265	mit dem Transistoren-Computer IBM 7090	8:43 h
Jean Guilloud, J. Filliatre	1966	250.000	IBM 7030	41:55 h
Jean Guilloud, M. Dichampt	1967	500.000	CDC 6600	28:10 h
Jean Guilloud, Martin Boyer	1973	1.001.250	CDC 7600	23:18 h
Kazunori Miyoshi, Yasumasa Kanada	1981	2.000.036	FACOM M-200	137:18 h
Jean Guilloud	1981	2.000.050
Yoshiaki Tamura	1982	2.097.144	MELCOM 900II	7:14 h
Yoshiaki Tamura, Yasumasa Kanada	1982	4.194.288	HITAC M-280H	2:21 h
Yoshiaki Tamura, Yasumasa Kanada	1982	8.388.576	HITAC M-280H	6:52 h
Yasumasa Kanada, Sayaka Yoshino, Yoshiaki Tamura	1982	16.777.206	HITAC M-280H	< 30 h
Yasumasa Kanada, Yoshiaki Tamura, Yoshinobu Kubo	1987	134.217.700
David und Gregory Chudnovsky	1989	1.011.196.691
Yasumasa Kanada, Daisuke Takahashi	1997	51.539.600.000
Yasumasa Kanada, Daisuke Takahashi	1999	206.158.430.000
Yasumasa Kanada	2002	1.241.100.000.000	Berechnung: $\pi = 48 \arctan \tfrac{1}{49} + 128 \arctan \tfrac{1}{57} - 20 \arctan \tfrac{1}{239} + 48 \arctan \tfrac{1}{110443}$ Verifikation: $\pi = 176 \arctan \tfrac{1}{57} + 28 \arctan \tfrac{1}{239} - 48 \arctan \tfrac{1}{682} + 96 \arctan \tfrac{1}{12943}$
Daisuke Takahashi	2009	2.576.980.370.000	Berechnung: Gauß-Legendre-Algorithmus
Fabrice Bellard	2010	2.699.999.990.000	Berechnung: TachusPi Software (Chudnovsky-Formel, Verifikation: Bellards Formel)	131 Tage
Shigeru Kondo, Alexander Yee	2010	5.000.000.000.000	Berechnung: y-cruncher Software (Chudnovsky-Formel, Verifikation: Plouffes und Bellards Formel)	090 Tage
Shigeru Kondo, Alexander Yee	2011	10.000.000.000.050	Berechnung: y-cruncher Software (Chudnovsky-Formel, Verifikation: Plouffes und Bellards Formel)	191 Tage
Shigeru Kondo, Alexander Yee	2013	12.100.000.000.050	Berechnung: y-cruncher Software (Chudnovsky-Formel, Verifikation: Bellards Formel)	082 Tage
Sandon Van Ness (Houkouonchi)	2014	13.300.000.000.000	Berechnung: y-cruncher Software (Chudnovsky-Formel, Verifikation: Bellards Formel)	208 Tage
Peter Trüb	2016	22.459.157.718.361	Berechnung: y-cruncher Software (Chudnovsky-Formel, Verifikation: Bellards Formel)	105 Tage
Emma Haruka Iwao / Google LLC	2019	31.415.926.535.897	Berechnung: y-cruncher Software (Chudnovsky-Formel, Verifikation: Plouffes und Bellards Formel)	121 Tage
Timothy Mullican	2020	50.000.000.000.000	Berechnung: y-cruncher Software (Chudnovsky-Formel, Verifikation: Plouffes und Bellards Formel)	303 Tage

Alternative Kreiszahl τ

Der amerikanische Mathematiker Robert Palais schlug 2001 in einer Ausgabe des Mathematik-Magazins The Mathematical Intelligencer vor, für $\pi$ , statt wie bisher den Quotienten aus Umfang und Durchmesser eines Kreises, in Zukunft den Quotienten aus Umfang und Radius (entsprechend $2\pi$ ) als grundlegende Konstante zu verwenden. Seine Argumentation beruht darauf, dass in vielen mathematischen Formeln der Faktor vor der Kreiszahl auftauche. Ein weiteres Argument ist die Tatsache, dass die neue Konstante im Bogenmaß einen Vollwinkel darstellt, statt wie $\pi$ einen halben Winkel, und so weniger willkürlich wirkt. Die neu normierte Kreiszahl, für deren Notation Michael Hartl und Peter Harremoës den griechischen Buchstaben $\tau$ (Tau) vorschlugen, würde diese Formeln verkürzen. Nach dieser Konvention gilt dann $\tau =2\pi =6{,}283185\ldots$ , also $\pi ={\tfrac {\tau }{2}}$ .

Literatur

Jörg Arndt, Christoph Haenel: Π [Pi]. Algorithmen, Computer, Arithmetik. 2., neu bearbeitete und erweiterte Auflage. Springer Verlag, Berlin 2000, ISBN 3-540-66258-8 ISBN 3-540-63419-3.
Ehrhard Behrends (Hrsg.): Π [Pi] und Co. Kaleidoskop der Mathematik. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77888-2.
Egmont Colerus: Vom Einmaleins zum Integral. Mathematik für Jedermann (= rororo-Sachbuch. Nr. 6692). Rowohlt, Reinbek bei Hamburg 1974, ISBN 3-499-16692-5.
Keith Devlin: Sternstunden der modernen Mathematik. berühmte Probleme und neue Lösungen (= dtv-Taschenbuch 4591). 2. Auflage. Deutscher Taschenbuch Verlag, München 1992, ISBN 3-423-04591-4 (Originaltitel: Mathematics. Übersetzt von Doris Gerstner, Lizenz des Birkhäuser-Verlags, Basel).
Eberhard Freitag, Rolf Busam: Funktionentheorie 1 (= Springer-Lehrbuch). 3., neu bearbeitet und erweiterte Auflage. Springer Verlag, Berlin (u.a.) 2000, ISBN 3-540-67641-4.
Konrad Knopp: Theorie und Anwendung der unendlichen Reihen (= Die Grundlehren der Mathematischen Wissenschaften. Band 2). 5., berichtigte Auflage. Springer Verlag, Berlin (u.a.) 1964, ISBN 3-540-03138-3.

Anmerkungen

↑ Mathematisch streng gilt $\pi >3{,}14$ .
↑ Einen einfachen Irrationalitätsbeweis lieferte im Jahre 1947 der Zahlentheoretiker Ivan Niven. (Ivan Niven: A simple proof that π is irrational. In: Bulletin of the American Mathematical Society. Band 53, 1947, S. 509.
↑ Hier sind alle Teilzähler gleich 1.
↑ Hier sind alle Teilzähler gleich −1.
↑ Dabei ist $n=2{,}84438\dotso \cdot 10^{226}.$
↑ Die Euler-Identität wird als Kombination der Kreiszahl $\pi$ , der ebenfalls transzendenten eulerschen Zahl , der imaginären Einheit $\mathrm {i}$ und der beiden algebraischen Basisgrößen $0$ und als eine der „schönsten mathematischen Formeln“ angesehen.

Basierend auf einem Artikel in:

Wikipedia.de