Riemannsche ζ-Funktion
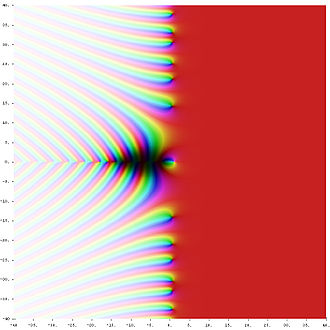
Die riemannsche ζ-Funktion (Zeta-Funktion nach Bernhard Riemann) ist eine spezielle mathematische Funktion, die in der analytischen Zahlentheorie, einem Teilgebiet der Mathematik, eine zentrale Rolle spielt. Ihre entscheidende Bedeutung erlangt die riemannsche ζ-Funktion durch den Zusammenhang zwischen der Lage ihrer komplexen Nullstellen und der Verteilung der Primzahlen. Die genaue Lage dieser Nullstellen ist Gegenstand der riemannschen Vermutung, eines der wichtigsten ungelösten Probleme der Mathematik. Ausgehend von einer Definition als Dirichlet-Reihe findet die riemannsche ζ-Funktion in zahlreichen mathematischen Disziplinen Anwendung:
- in der analytischen Zahlentheorie im Zusammenhang mit Primzahlen, zahlentheoretischen Funktionen und weiteren Dirichlet-Reihen,
- in der Analysis durch besondere Funktionswerte und das Auftreten in unendlichen Reihen sowie
- in der Wahrscheinlichkeitstheorie, zum Beispiel bei der Zeta-Verteilung.
Erstmals untersucht wurde die Zeta-Funktion im 18. Jahrhundert von Leonhard Euler, der bedeutende Aussagen bezüglich ihrer fundamentalen Eigenschaften treffen konnte. In der Zeit danach folgten viele weitere Entdeckungen, die bedeutendsten unter ihnen von Riemann im Jahr 1859, der den tiefgründigen Zusammenhang zwischen der Zeta-Funktion und den Primzahlen erheblich erweiterte. Entscheidende Fortschritte erzielten Mathematiker wie zum Beispiel Ernst Leonard Lindelöf, Jacques Hadamard, Charles-Jean de La Vallée Poussin, Godfrey Harold Hardy, John Edensor Littlewood, Atle Selberg, Sergei Michailowitsch Woronin und John Brian Conrey. Wegen der überragenden Bedeutung der riemannschen Vermutung für die Zahlentheorie und deren Anwendungen bleibt der Themenkreis der riemannschen ζ-Funktion ein Gebiet intensiver mathematischer Forschung.
Einordnung ohne mathematisches Vorwissen
Im Zentrum der Zahlentheorie, jenes Zweiges der Mathematik, der sich mit den Eigenschaften der ganzen Zahlen 1, 2, 3, 4 ... beschäftigt, stehen die Primzahlen 2, 3, 5, 7, 11, .... Diese sind ausgezeichnet durch die Eigenschaft, genau zwei Teiler zu haben, nämlich die 1 und sich selbst. Die 1 ist keine Primzahl. Bereits Euklid konnte zeigen, dass es unendlich viele Primzahlen gibt, weshalb die Liste 2, 3, 5, 7, 11, ... niemals enden wird.
Die Primzahlen sind gewissermaßen die Atome
der ganzen Zahlen, da sich jede positive ganze Zahl eindeutig in solche zerlegen
lässt. Zum Beispiel ist
und
.
Trotz dieser elementaren Eigenschaft ist nach mehreren Jahrtausenden
Mathematikgeschichte bis heute kein einfaches Muster bekannt, dem sich die
Primzahlen in ihrer Folge unterwerfen. Ihre Natur ist eines der größten
mathematischen Rätsel.
Auch wenn das detaillierte Verständnis der Sequenz 2, 3, 5, 7, ... unerreichbar fern ist, kann man nach Mustern suchen, wenn man den Blick ausweitet. Zum Vergleich stelle man sich vor, dass mit Hilfe statistischer Methoden das Verhalten sehr vieler Menschen (zum Beispiel bezüglich Konsum- und Wahlverhalten) oft überraschend präzise beschrieben werden kann, obgleich ein einzelner Mensch äußerst komplex ist. Das hat grob gesagt damit zu tun, dass größer werdende relevante Datenmengen immer zuverlässigere Informationen liefern. Im Falle der Primzahlen führt eine solche Ausweitung unter anderem zu der Frage, wie viele Primzahlen es unter einer fest gewählten Zahl gibt.
Zum Beispiel sind nur 4 Primzahlen, nämlich 2,3,5 und 7, kleiner als die Zahl 10. Im Falle von 50 sind es schon 15 kleinere Primzahlen, sie sind gegeben durch
Ende des 19. Jahrhunderts konnte ein verblüffend einfaches (allerdings grobes) Beschreibungsmuster für das quantitative Verhalten der Primzahlen unter einer Größe bewiesen werden. Dieses wurde bereits im 18. Jahrhundert vom 15-jährigen Gauß vermutet. Aus diesem lässt sich aus einer gegebenen Zahl die Anzahl der Primzahlen, die kleiner als diese Zahl sind, schätzen. Das Muster wird relativ betrachtet immer genauer, je größer die obere Schranke gewählt wird. Beispielsweise liefert es für den Wert 50 die Prognose 18 (es sind tatsächlich 15 Primzahlen, siehe oben). Weiter sagt es rund 1246 Primzahlen unter der Zahl 10.000 voraus - tatsächlich sind es 1229.
Das entscheidende Werkzeug zum Beweis dieses schätzungsweise richtigen Musters ist die riemannsche Zeta-Funktion. Das besondere an dieser Funktion ist, dass sie das Gesetz der eindeutigen Primfaktorzerlegung in der Sprache der Analysis ausdrückt. Interessanterweise erhöht sich mit dem Wissen um die Zeta-Funktion auch unser Wissen um die Primzahlen, sogar in detaillierteren Fragestellungen. So können viele Primzahltests, wie der von Miller-Rabin unter Annahme der riemannschen Vermutung bewiesen bzw. verbessert werden. Die Nullstellen der Zeta-Funktion implizieren zudem einen Korrekturterm oberen Musters, der es in einen exakten Ausdruck umwandelt. Jedoch sind praktische Berechnungen mit dieser Formel numerisch nicht sinnvoll.
Die Primzahlen sind nicht nur Gegenstand der mathematischen Grundlagenforschung, sondern haben auch Anwendung. So kommen beispielsweise bei diversen Kryptosystemen wie der RSA-Verschlüsselung sehr große Primzahlen zum Einsatz.
Geschichte
Im Gegensatz zu den Primzahlen oder der euklidischen Geometrie ist die mathematische Entdeckungsgeschichte der riemannschen Zetafunktion sehr jung. So sind alle bis heute wesentlichen Entdeckungen zu dieser Funktion in den letzten 350 Jahren gemacht worden. Dies liegt zum einen daran, dass in der Zeit davor die notwendigen mathematischen Methoden noch nicht ausgereift waren. Die Zeta-Funktion besaß zum Zeitpunkt ihrer Entdeckung noch keinerlei offensichtliche Anwendung in der Praxis. Ein Grund, weshalb sie trotzdem die Aufmerksamkeit vieler Mathematiker erhielt, war, dass sie trotz ihrer sehr simpel wirkenden Struktur nicht so triviale Eigenschaften besitzt wie beispielsweise die geometrische Reihe.

Einer der ersten Mathematiker, der sich mit einem Vorläufer der heute definierten Zeta-Funktion intensiv und ausführlich auseinandersetzte, war Leonhard Euler. Seit Beginn des 18. Jahrhunderts versuchten Mathematiker, den exakten Grenzwert der unendlichen Reihe
zu bestimmen. Leonhard Euler, der im Jahre 1735 dieses schwierige Basler Problem mit Hilfe eigener neuartiger Techniken löste, untersuchte anschließend den verallgemeinerten Ausdruck
(Euler verwendete das „reelle “,
die Schreibweise mit komplexer Variablen
wurde erst über Riemann populär) in der Hoffnung, weitere und außerdem weit
bedeutendere Aussagen über diese Reihe treffen zu können.
Da die Methoden der komplexen Analysis
Euler zu seinen Lebzeiten weitestgehend noch nicht bekannt waren, war er auch
noch nicht im Stande, das Problem der Primzahlen in der Weise anzugehen wie
später Riemann. Jedoch gelangen ihm einige wichtige Aussagen.

So fand er zum Beispiel die Lösung des Basler Problems und die allgemeine Formel
(Euler selbst verwendete noch nicht das
als Funktionssymbol) und berechnete neben
per Hand
den Wert
Auch entdeckte Euler das nach ihm benannte Euler-Produkt
und konnte mit seiner Hilfe die Divergenz der Reihe der Kehrwerte aller Primzahlen
nachweisen. Diese Tatsache war für ihn ein Indikator dafür, dass Primzahlen wesentlich dichter liegen müssten als Quadratzahlen, da er im Basler Problem ja gezeigt hatte, dass die unendliche Summe der Kehrwerte aller Quadratzahlen gegen einen endlichen Grenzwert strebt. Auch die von Riemann später bewiesene Funktionalgleichung soll Euler schon bekannt gewesen sein.

Im Jahr 1859 setzte Bernhard Riemann in seiner
Arbeit Über die Anzahl der Primzahlen unter einer gegebenen Größe die
Zeta-Funktion in zentralen Zusammenhang zu den Primzahlen. Zwar hatte Euler
schon ein Jahrhundert zuvor die Gültigkeit des Euler-Produktes aufgezeigt,
jedoch war es erst mit Riemanns Herangehensweise möglich geworden, daraus
konkrete Informationen über Primzahlen selbst zu gewinnen. Riemann, der selbst
ein Schüler von Gauß
war, schrieb in seiner achtseitigen Arbeit eine funktionentheoretische
Interpretation und Auswertung des Euler-Produkts, die einen Zusammenhang
zwischen Primzahlen und den nicht-trivialen Nullstellen der Zeta-Funktion
schaffte. Damit war ihm ein völlig neuer Zugang zu dem Primzahl-Rätsel gelungen.
In ihr führte er auch zum ersten Mal das griechische
(Zeta) als
Funktionssymbol ein. In seiner Arbeit formulierte er außerdem seine bis heute
unbewiesene berühmte riemannsche
Vermutung, die eine wichtige Aussage über die genaue Lage der Nullstellen
der Zeta-Funktion macht. Daher beschäftigte sich Riemann ebenfalls mit der
numerischen Berechnung seiner Zeta-Funktion und fand sogar die ziemlich genaue
Lage einiger nicht-trivialer Nullstellen in der komplexen Ebene, ohne dafür eine
Rechenmaschine zu benutzen. Seine Formel wurde später von dem deutschen
Mathematiker Carl Ludwig Siegel bei der Auswertung seiner Dokumente wiederentdeckt und wird
seit diesem Zeitpunkt Riemann-Siegel-Formel
genannt.
Da viele von Riemanns Aufzeichnungen nach seinem Ableben von seiner Haushälterin verbrannt wurden, kann bis heute nur spekuliert werden, wie weit seine Untersuchungen tatsächlich gingen.
Im Jahre 1910 veröffentlichte der indische Mathematiker S. Ramanujan im Journal of the Indian Mathematical Society einen Artikel, in dem unter anderem die folgende Gleichung behauptet wurde:
Die meisten Mathematiker, die diese Gleichung zu Gesicht bekamen, hatten sie als offensichtlichen Schwachsinn gewertet. So kam es, dass Professor Hill vom University College in London schrieb:
„Mr. Ramanujan ist ein Opfer der Fallstricke des sehr schwierigen Gebietes der divergenten Reihen geworden.“
Als Ramanujan jedoch den britischen Mathematiker Godfrey Harold Hardy in Cambridge
brieflich auf seine Theorie aufmerksam machte, wurde diesem in der Gleichung die
korrekte Auswertung des Werts
bewusst, auch wenn sie bezüglich ihrer mathematischen Formalität natürlich
inkorrekt war. Hardy war sich sicher, dass Ramanujan, trotz seiner fremden Art,
Mathematik zu betreiben, ein Genie sein müsse.
Definition
Die Zeta-Funktion wird in der Literatur generell über ihre Darstellung als Dirichlet-Reihe definiert.
Für komplexe
Zahlen ,
deren Realteil
größer als 1 ist, ist die Zeta-Funktion definiert durch die Dirichlet-Reihe
Wie man leicht über das Integralkriterium
für unendliche Reihen beweist, ist diese Reihe im angegebenen Bereich absolut
konvergent. Zudem ist die Konvergenz auf kompakten Teilmengen
gleichmäßig, weshalb nach dem Satz
von Weierstraß die dargestellte Funktion holomorph ist.
Wegen der Divergenz der harmonischen
Reihe ist diese Darstellung für alle komplexen Zahlen mit Realteil kleiner
oder gleich 1 jedoch ungültig. In besonderem Maße wird dies für negative
Argumente ersichtlich, wenn man zum Beispiel versuchte, die -Funktion
an der Stelle
über die Dirichlet-Reihe auszuwerten. Man hätte dann
und diese Reihe hat offensichtlich keinen endlichen Grenzwert.
Die Dirichlet-Reihe wird aufgrund ihrer Einfachheit und ihrer
zahlentheoretischen Relevanz (siehe Euler-Produkt) als Basisdefinition
verwendet. Mittels analytischer
Fortsetzung wird eine sinnvolle Berechnung für alle komplexen Zahlen mit
Ausnahme der Zahl
möglich. Damit können schließlich auch scheinbar unendlich großen Werten wie
einen Sinn gegeben werden, es gilt zum Beispiel
.
Euler-Produkt
Eine wesentliche Eigenschaft der Zeta-Funktion ist ihre Verbindung zu den Primzahlen.
Euler, der als Erster
diesen Zusammenhang entdeckte, betrachtete dafür das später nach ihm benannte
Euler-Produkt,
welches für alle
mit
gültig ist:
Hierbei stellt jeder einzelne Faktor des Produktes eine geometrische
Reihe
gebildet über den Wert
dar, während sich das gesamte Produkt über alle Primzahlen
erstreckt. Das Euler-Produkt ist deshalb so erstaunlich, da Primzahlen aufgrund
ihrer chaotischen Verteilung sehr schwer in analytischen Ausdrücken
unterzubringen sind. Jedoch stellt es eine überraschend einfache Identität
zwischen den „chaotischen Primzahlen“ und einer wohlgeordneten Reihe dar. In der
Tat, lässt sich das Euler-Produkt als analytische Version des Gesetzes der
eindeutigen Primfaktorzerlegung interpretieren.
Zum Beweis betrachtet man für eine Schranke
zunächst
Da jeder Faktor eine geometrische Reihe ist, gilt
für alle Primzahlen .
Dann gilt aber auch
wobei der Strich an der zweiten Summe anzeigt, dass nur über alle
summiert wird, deren Primteiler sämtlich
sind. Daraus folgt:
und mit
und
folgt die Behauptung.
Aus der unbedingten Konvergenz des Euler-Produktes folgt unmittelbar, dass
auf der Halbebene
keine Nullstellen besitzt. Ferner gilt dort die Identität
woraus Riemann schließlich den für alle
gültigen, zahlentheoretisch sehr wichtigen Ausdruck
hervorbringen
konnte. Hierbei bezeichnet
die Primzahlfunktion, welche zählt, wie viele Primzahlen kleiner als
sind. Die Summe auf der linken Seite liefert für jede Primzahlpotenz
jeweils den Beitrag
,
kann also mit
identifiziert werden.
Analytische Fortsetzung
Eine analytische
Fortsetzung der im Gebiet
durch die Reihe
definierten holomorphen
Funktion ist eine auf einem größeren Gebiet
holomorphe Funktion, welche auf ganz
mit dieser übereinstimmt. Nach dem Identitätssatz
für holomorphe Funktionen ist eine solche Fortsetzung stets eindeutig
bestimmt.
Obwohl es für den ganz allgemeinen Fall kein konstruktives Verfahren gibt,
analytische Fortsetzungen anzugeben, ist es durch die Einfachheit der
Dirichlet-Reihe
nicht schwierig, eine solche zu finden. Besonders einfach erweist sich dies für
die gelochte Halbebene
,
mittels der Beobachtung
Die Reihe zur rechten konvergiert nachweislich in besagter erweiterten
Halbebene und wird in der Literatur auch manchmal als dirichletsche
Eta-Funktion
bezeichnet. Für eine weitere holomorphe Ausdehnung des Definitionsbereiches
eignen sich nun viele Methoden, welche jedoch nach dem Identitätssatz alle
dieselbe Funktion darstellen. Eine davon bietet die Anwendung der
eulerschen
Reihentransformation auf die obere alternierende Reihe. Man erhält damit
eine 1930 von Konrad Knopp veröffentlichte und auf ganz
definierte Reihenidentität
Diese wurde von Helmut Hasse bewiesen. Es ist zu beachten, dass die anderen Singularitäten
mit
sämtlich hebbar
sind.
Funktionalgleichung
Im Folgenden bezeichnet
die Gammafunktion, die die Fakultät
auf komplexe Zahlen verallgemeinert. Auf ganz
gilt als Identität zwischen meromorphen
Funktionen
Aus dieser geht durch einfache Umformung die alternative Darstellung
für alle
hervor. Oft wird auch die symmetrische Variante der Funktionalgleichung,
nämlich
in der Literatur zitiert. Man beachte die Invarianz, die unter der
Variablentransformation
entsteht.
Die Funktionalgleichung schafft einen Zusammenhang zwischen bedeutenden mathematischen Funktionen und zieht wichtige Resultate nach sich. So bietet sie beispielsweise wertvolle Erkenntnisse über die Lage der Nullstellen der Zeta-Funktion, die in direktem Zusammenhang zu den Primzahlen stehen.
Alternativ zu der obigen Funktionalgleichung definierte Riemann in seiner Arbeit die Funktion
für die
gilt. Sie wird auch als riemannsche Xi-Funktion bezeichnet.
Ein Herleitungsansatz für die Funktionalgleichung befindet sich im Abschnitt Beziehung zur Thetafunktion.
Eigenschaften
Meromorphie, Singularitäten und Laurent-Reihe
Die -Funktion
ist eine in ganz
holomorphe
Funktion, das bedeutet, dass sie an allen Stellen außer
komplex
differenzierbar ist.
Ihre
-te Ableitung besitzt für Argumente
mit Realteil größer als 1 die Darstellung:
An der Stelle
besitzt sie, aufgrund der Divergenz der harmonischen
Reihe, einen Pol
erster Ordnung mit Residuum
1, das heißt, es gilt:
Also ist sie eine in ganz
meromorphe
Funktion. Insbesondere kann sie um
in eine Laurent-Reihe
mit Konvergenzradius
entwickelt werden, diese hat die Form
Bei den Koeffizienten
handelt es sich um die Stieltjes-Konstanten,
wobei
die Euler-Mascheroni-Konstante
ist,
für die sich daraus insbesondere der Ausdruck
ergibt.
Asymptotisches Verhalten
Für unbegrenzt größer werdende Realteile hat die Zeta-Funktion ein leicht zu bestimmendes asymptotisches Verhalten, es gilt
Dies folgt unmittelbar aus der gleichmäßigen Konvergenz der Dirichlet-Reihe
in den Bereichen
und Vertauschung von Limes und Summation:
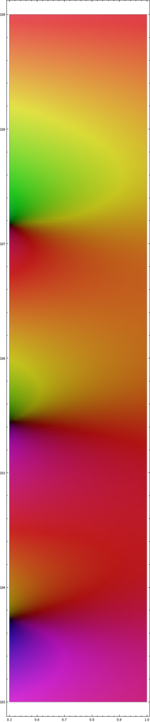
Vergleiche hierzu auch den komplexen Graphen der Zeta-Funktion zu Beginn des Artikels, der in Richtung der positiven reellen Achse zunehmend konstant rot gefärbt ist.
Wachstumsgesetze entlang der vertikalen imaginären Achse sind, falls vorhanden, deutlich schwerer zu sondieren. Jedoch sind einige Abschätzungen bekannt. Mit Hilfe des Phragmen-Lindelöf Prinzips zeigt man
für feste Werte
und alle
.
Dabei ist
eine positive Konstante. Diese Abschätzung kann jedoch vermutlich weiter
verbessert werden. Setzt man zu diesem Zweck
so wird zum Beispiel vermutet, dass
ist. Diese lindelöfsche
Vermutung folgt aus der Richtigkeit der riemannschen Vermutung, ist aber bis
heute unbewiesen.
Spiegelung konjugierter Argumente
Hinweis: Diese ist keine nur für die Zeta-Funktion spezifische Eigenschaft, spielt aber bezüglich der Verteilung der Nullstellen eine wichtige Rolle, weshalb sie trotzdem ausführlicher erwähnt wird.
Zu einer komplexen Zahl
definiert man ihre Konjugation
über
.
Es gilt nun für alle
:
Das bedeutet: Wenn für ein reelles Zahlenpaar
mit
mit
gilt, so gilt gleichzeitig
Das sieht man unmittelbar mit
- im Falle der analytischen Fortsetzung ist dies mit der Reihentransformation
weiterhin erfüllt. Ist nun
eine Nullstelle, so gilt insbesondere
weshalb
ebenfalls Nullstelle ist.
Charakterisierung durch Hamburger
Im Jahre 1921 gelang es Hans Hamburger, die riemannsche Zeta-Funktion anhand ihrer Funktionalgleichung wie folgt zu charakterisieren.
Es sei ,
wobei
eine ganze Funktion endlicher Ordnung und
ein Polynom ist, für
durch die Dirichlet-Reihe
darstellbar. Ferner gelte die Funktionalgleichung
wobei
ebenfalls auf der Halbebene
als Dirichlet-Reihe
darstellbar sei. Dann folgt bereits die Identität
.

Universalitätssatz von Woronin
Nach dem Universalitätssatz von Sergei Michailowitsch Woronin
ist die riemannsche -Funktion
imstande, jede beliebige (holomorphe) Funktion in einer nullstellenfreien
Kreisscheibe mit Radius 1/4 beliebig genau zu approximieren.
Als anschaulichen Vergleich stelle man sich dafür vor, dass es für jede (holomorphe) Funktion eine Art „Landkarte“ gibt, die Höhen und Tiefen sowie Himmelsrichtung der Funktionswerte in der komplexen Ebene darstellt. Der Universalitätssatz besagt nun, dass man, wenn man die Landkarte der Zeta-Funktion in einem bestimmten unendlichen Bereich scannen würde, früher oder später auf Gebiete stieße, die Ausschnitten der Landkarten anderer Funktionen, also mitsamt allen darin eingetragenen „Bergen“ und „Tälern“, sehr ähneln – ja, sogar beliebig genau ähneln. Als einzige Voraussetzung gelte hierbei jedoch, dass auf dem Kartenausschnitt der fremden Funktion nie der Wert 0 eingetragen sei.
Formal ausgedrückt: sei
eine zusammenhängende, kompakte
Teilmenge des Streifens
.
Sei
nun eine in ganz
holomorphe Funktion, die außerdem für kein
verschwinde. Es existiert dann für jedes
ein
,
sodass
für alle .
Wenn es nun kein
gibt, derart dass
ist, die Approximation also nicht perfekt möglich ist und trotzdem immer besser
werden soll, indem
immer kleiner wird, muss
immer größer werden. Dabei kann
nicht den Limes
haben, sondern höchstens ein Häufungspunkt
sein.
Es gilt sogar noch mehr: die Dichte aller ,
die eine Approximation erfüllen, ist positiv, wie folgende Ungleichung
beweist. Hier ist
das Standard-Lebesgue-Maß
auf den reellen Zahlen.
Mellin-Transformation - die Verbindung zur Gamma-Funktion
Die nach der Definition als Dirichlet-Reihe und dem Euler-Produkt wohl elementarste und wichtigste Darstellung der Zeta-Funktion ist die sogenannte Mellin-Transformation. Dabei wird die Zeta-Funktion über ein unendliches Integral ausgedrückt.
Grundlage dieser Darstellung ist das eulersche Integral für die Gamma-Funktion
aus welchem nach der Substitution
mit
und Division durch
nach beidseitigem Summieren der Ausdruck
hervorgeht. Dieser gilt naturgemäß nur auf der Halbebene .
Zu beachten ist jedoch, dass der Integrand neben der Kernfunktion
eine um
analytische Funktion ist:
Diese Tatsache schafft eine enge Beziehung zwischen Zeta-Funktion und den Bernoulli-Zahlen .
Durch sukzessives Abspalten der Taylor-Polynome von
im Integrationsintervall von 0 bis 1 kann die Zeta-Funktion auf ganz
fortgesetzt werden:
Dabei wird ausgenutzt, dass
eine ganze
Funktion ist. Wertet man die hebbaren
Singularitäten (durch Limesbildung) and den Stellen
aus, offenbart sich der enge Zusammenhang zwischen
und den Bernoulli-Zahlen.
Eng verwandt zur oberen Transformation ist eine Kurvenintegraldarstellung.
Diese wurde von Riemann selbst verwendet, um die Zeta-Funktion in die komplexe
Ebene fortzusetzen. Indem er den Integrationsweg des Mellin-Integrals aus dem
oberen Abschnitt modifizierte, konnte Riemann für alle
herleiten, wobei "der Integrationsweg
von +∞ nach +∞ verläuft und den Ursprung einmal umläuft". Gemeint ist damit ein
Weg, der von +∞ knapp über der reellen Achse parallel Richtung Ursprung
verläuft, diesen entgegen Uhrzeigerrichtung
umkreist, und anschließend unterhalb der reellen Achse wieder zu +∞ strebt.
Über eine inverse Mellin-Transformation lässt sich oberer Integrand aus der
Zeta-Funktion zurück gewinnen. Es gilt für jede reelle Zahl
und alle
:
Der tiefe Zusammenhang zwischen der Zeta-Funktion und der Fakultät wurde bereits von Euler beobachtet, jedoch nicht mathematisch rigoros ausgearbeitet.
Spezielle Funktionswerte
Funktionswerte für gerade natürliche Zahlen
Die Funktionswerte der riemannschen Zeta-Funktion für positive gerade Zahlen
haben eine enge Beziehung zur Kreiszahl
.
Für eine positive ganze Zahl
ist
wobei
die
-te
Bernoulli-Zahl
bezeichnet. Somit lässt sich jeder Funktionswert
in der Form
schreiben, wobei
und
ganze Zahlen sind. Daraus folgt auch sofort, dass jeder Wert
für natürliche Zahlen
irrational
und sogar transzendent
ist.
Beispielsweise ist
Diese Formeln wurden von Euler
entdeckt und 1735 in seiner Arbeit De Summis Serierum Reciprocarum
erstmals veröffentlicht. Das Auffinden des Werts von
ist auch als das Basler
Problem bekannt.
Daneben gibt es auch die bemerkenswerte Rekursionsformel
für natürliche Zahlen ,
die Euler noch nicht bekannt war.
Funktionswerte für ungerade natürliche Zahlen
Über den Wert der Zeta-Funktion für ungerade natürliche Zahlen ist nur sehr
wenig bekannt. Beispielsweise weiß man, dass die Apéry-Konstante
irrational ist, was 1979 von dem französischen Mathematiker Roger Apéry bewiesen
wurde.
Sein Beweis fand große Achtung in den Mathematikerkreisen – z.B. zitierte
Carl Ludwig Siegel:
„Man kann den Beweis nur wie einen Kristall vor sich hertragen“
Im Wesentlichen verwendete Apéry die Reihe
mit rationalen Gliedern. Es gilt hingegen auch .
Somit geriet die Frage nach der Existenz rationaler Zahlen
mit
oder auch
zunehmend in den Mittelpunkt, um Aperys Beweismethode gegebenenfalls auch auf andere Zeta-Werte anwenden zu können. Diese ist bis heute nicht geklärt, aber Gegenstand intensiver Forschung.
Es ist hingegen sehr wohl bekannt, dass unendlich viele Werte
irrational sind.
Außerdem konnte Wadim Zudilin als Spezialfall zeigen, dass mindestens einer der
Werte
,
,
und
irrational sein muss.
Um 1900 fand Matyáš Lerch
einen besonders eleganten Ausdruck für :
Durch Arbeiten von Lerch und S. Ramanujan inspiriert, entwickelte der Kanadier Simon Plouffe ab 1995 weitere Ausdrücke dieser Art:
Diese Ausdrücke eignen sich für eine effiziente Berechnung der Zetawerte sehr gut, da die einbezogenen Reihen äußerst schnell konvergieren.
Eine allgemeine Formel für alle ungeraden positiven ganzen Zahlen der Form
mit
ist:
wobei
die
-te
Bernoulli-Zahl ist. Dies
vereinfacht sich zu einer alternativen Darstellung, die Zeta-Werte gerader
Argumente mit einschließt:
Somit lässt sich jeder Wert
in der Form
mit ganzen Zahlen
und
schreiben, was, ähnlich bei den Werten gerader Funktionsargumente, eine engere
Verwandtschaft zwischen
und
impliziert. Es ist jedoch bis heute ungeklärt, ob einer der Werte
als rationales Vielfaches von
darstellbar ist.
Es gibt noch eine Multiintegraldarstellung für natürliche Argumente. Für alle
erhält man:
So bekommt man unter anderem:
Dies beweist man leicht durch die Auffassung des Integranden als Grenzwert der geometrischen Reihe und Vertauschung von Integration und Summation.
| 2n + 1 | ζ(2n + 1) | OEIS Folge |
|---|---|---|
| 3 | 1,2020569031595942853997381… | Folge A002117 in OEIS |
| 5 | 1,0369277551433699263313654… | Folge A013663 in OEIS |
| 7 | 1,0083492773819228268397975… | Folge A013665 in OEIS |
| 9 | 1,0020083928260822144178527… | Folge A013667 in OEIS |
| 11 | 1,0004941886041194645587022… | Folge A013669 in OEIS |
| 13 | 1,0001227133475784891467518… | Folge A013671 in OEIS |
| 15 | 1,0000305882363070204935517… | Folge A013673 in OEIS |
| 17 | 1,0000076371976378997622736… | Folge A013675 in OEIS |
| 19 | 1,0000019082127165539389256… | Folge A013677 in OEIS |
Funktionswerte für nichtpositive ganze Zahlen
Im Gegensatz zu den Zeta-Werten positiver ganzer Argumente, über die im Falle der ungeraden Werte bis heute nahezu nichts bekannt ist, sind die Funktionswerte für nichtpositive ganze Zahlen sämtlich bekannt. Insbesondere sind sie alle rational. Sie hängen, wie die Zeta-Werte gerader positiver Zahlen, sehr eng mit den Bernoulli-Zahlen zusammen.
Aus der Funktionalgleichung und Eulers Formel für gerade Zeta-Werte gelangt
man für eine natürliche Zahl
zu:
Aus
für ungerade n sowie
was ebenfalls aus der Funktionalgleichung folgt, geht schließlich die für
alle natürlichen Zahlen
gültige Darstellung
hervor. Weitere Werte sind:
Bezüglich des Wertes
schrieb der indische Mathematiker S. Ramanujan in einem seiner Artikel die
(formal natürlich inkorrekte) Gleichung:
siehe auch im Abschnitt Geschichte.
Funktionswerte für halbzahlige Argumente
Für die Funktionswerte für halbzahlige Argumente gilt:
(Folge A059750 in OEIS),
(Folge A078434 in OEIS).
Dieser Wert wird u.a. in der Physik bei der Berechnung der kritischen Temperatur für die Ausbildung eines sogenannten Bose-Einstein-Kondensats und in der Spinwellen-Theorie bei magnetischen Systemen benötigt.
2017 gab Franke folgende Identität für halbzahlige Funktionswerte:
mit ,
,
,
und
.
Spezielle Werte der Ableitung
Für alle negativen ganzen Zahlen
erhält man insbesondere:
Daraus ergeben sich unter anderem die Werte:
Andere Werte sind:
wobei
hier die Glaisher-Kinkelin-Konstante
bezeichnet.
Nullstellen
Die Lage der Nullstellen der riemannschen Zeta-Funktion hängt stark mit der
Verteilung der Primzahlen zusammen. Beispielsweise folgt aus der Aussage, dass
für alle
bereits der Primzahlsatz.
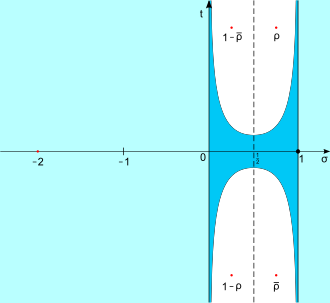
Triviale Nullstellen
Aus der Darstellung als Euler-Produkt kann man leicht folgern, dass
für
gilt. Zusammen mit der Funktionalgleichung
ergibt sich, dass die einzigen Nullstellen außerhalb des kritischen
Streifens
die „trivialen“ Nullstellen
sind.
Nicht-triviale Nullstellen
Neben den trivialen Nullstellen besitzt die Zeta-Funktion weitere Nullstellen
im kritischen Streifen .
Diese werden auch als nicht-triviale Nullstellen bezeichnet. Das hat den
Grund, dass bis heute nur sehr wenig über die genaue Lage dieser Nullstellen
bekannt ist. Dies hat unter anderem den Grund, dass das Euler-Produkt in dieser
Region nicht mehr konvergiert.
Nullstellenfreie Regionen
Bereits Ende des 19. Jahrhunderts konnte mit Hilfe eines einfachen Widerspruchsbeweises
gezeigt werden, dass die Zeta-Funktion keine Nullstellen auf der Geraden
besitzt. Diese nullstellenfreie Region konnte (teils mit großem analytischen
Aufwand) verbessert werden. Das bis heute schärfste nullstellenfreie Gebiet ist
für
gegeben durch:
Solche Verbesserungen führen (in verallgemeinerter Form für Dirichletsche L-Funktionen) unter anderem zum Satz von Siegel-Walfisz.
Spiegelung der Nullstellen
Die Funktionalgleichung der Zeta-Funktion und ihre grundlegende
Spiegelungseigenschaft bezüglich konjugierter Argumente implizieren ein
paarweises Auftreten der nicht-trivialen Nullstellen. Ist z.B.
eine Nullstelle im kritischen Streifen, so ist aufgrund der Funktionalgleichung
auch
Nullstelle. Zusätzlich aber ist
,
weshalb auch
Nullstelle ist; analog aber auch
Zu bemerken ist, dass alle Werte
und
im kritischen Streifen liegen, dort zu einem Rechteck verbunden werden können
und somit quasi ein Nullstellen-Doppelpaar bilden.
Ist jedoch die riemannsche
Vermutung richtig, so liegen alle Nullstellen auf der Geraden ,
wobei dann stets
bzw.
gilt.
Asymptotische Verteilung
Das Verteilungsmuster der Nullstellen entlang des kritischen Streifens ist
nicht vollkommen zufällig. Ähnlich wie bei den Primzahlen, die auf den ersten
Blick völlig willkürlich unter den natürlichen Zahlen verstreut sind, lässt sich
auch hier eine einfache Funktion finden, die zumindest asymptotisch die Streuung
darstellt und nachvollzieht. So kann man für eine gegebene Zahl
ein annäherndes Ergebnis auf die Frage finden, wie viele Nullstellen sich im
Bereich zwischen der reellen Achse und der Gerade
werden finden lassen. Riemann gab in seiner Arbeit diese Formel zur
asymptotischen Verteilung der nicht-trivialen Nullstellen erstmals an. Er
behauptete, die Anzahl
der Nullstellen innerhalb des Rechtecks
erfülle die asymptotische Äquivalenz
wobei der relative Fehler die Größenordnung
besitzt. Seinen Gedankengang begründete er über eine Auswertung des nullstellenzählenden
Integrals
wobei
die riemannsche
Xi-Funktion bezeichnet, die insbesondere dieselben Nullstellen im kritischen
Streifen besitzt wie die Zeta-Funktion. Unglücklicherweise fand sich in seinen
Aufzeichnungen aber kein einziger Hinweis, wie er dieses Integral berechnet
hatte. Da Riemann ein Genie auf dem Gebiet funktionentheoretischer Umformungen
war, geht man davon aus, dass er die Auswertung schlicht für zu trivial hielt,
um sie detailliert zu erklären. Das hatte zur Folge, dass Riemanns Herleitung
noch Jahre nach ihrer Veröffentlichung nur als Vermutung akzeptiert werden
konnte. Auch bezüglich anderer Aussagen fehlte es der Nachwelt an Beweisen.
Riemann ging nämlich noch weiter und behauptete die wesentlich stärkere Aussage,
dass die Anzahl der Nullstellen auf der kritischen Geraden
ebenfalls ungefähr bei seiner Auswertung von
läge. Bis heute kann nur spekuliert werden, wie er es schaffen konnte, solch
eine starke Aussage mit seinen Mitteln herzuleiten. Erst über 50 Jahre später
konnte Hans von Mangoldt
beweisen, dass Riemann zumindest bei seiner Angabe der Nullstellen im Rechteck
recht gehabt hatte.
Riemanns Aussagen über die Verteilung der Nullstellen auf der kritischen Gerade
sind jedoch wesentlich schwerer zu beweisen. Erst durch Arbeiten von Hardy,
Littlewood, Selberg und Levinson im 20. Jahrhundert gelangen erste wichtige
Einblicke und Erfolge.
Lage auf der kritischen Geraden


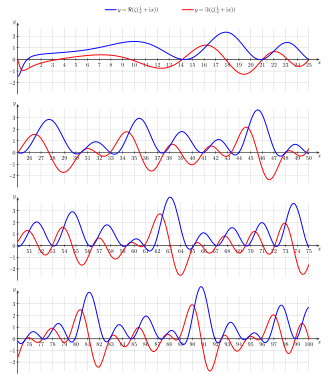
Im Jahr 1914 konnte Godfrey Harold Hardy zeigen, dass unendlich viele nicht-triviale Nullstellen auf der
kritischen Geraden
liegen. In seinem damals revolutionären Beweis machte er sich zu nutze, dass für
alle reellen Zahlenwerte
der Ausdruck
nur reelle Funktionswerte annimmt. Dies vereinfachte das Problem auf die zu
klärende Existenz unendlich vieler Nullstellen einer reellwertigen Funktion. Der
durch
Widerspruch geführte Beweis zeigt auf, dass
für
unendlich oft sein Vorzeichen wechseln muss, was schon zeigt, dass
unendlich viele Nullstellen auf
besitzt.
1921 verbesserte Hardy zusammen mit seinem Freund und Kollegen John Edensor Littlewood die Aussage auf das wesentlich stärkere Resultat, dass für
ausreichend große Werte
die Anzahl der Nullstellen auf der kritischen Geraden im Segment
mindestens
beträgt, wobei
eine positive Konstante bezeichnet. Atle Selberg
verbesserte dieses Ergebnis 1942 auf
.
Für diesen und andere Beiträge wurde er im Jahre 1950 mit der Fields-Medaille geehrt.
Anfang der 1970er konnte Norman Levinson zeigen, dass mindestens ein Drittel der nicht-trivialen Nullstellen auf der kritischen Geraden liegen muss. Sein nur knapp dreiseitiger Beweis wird als wichtiger Schritt in Richtung einer noch unbekannten Lösung der riemannschen Vermutung gesehen.
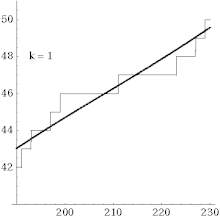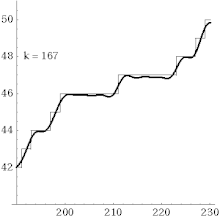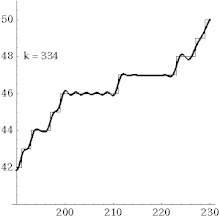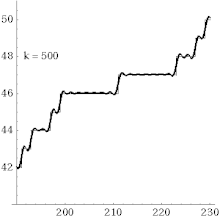
Explizite Berechnung der Primzahlfunktion
Über die nicht-trivialen Nullstellen kann der Wert der Primzahlfunktion
an der Stelle
explizit und exakt berechnet werden. Riemann führt die zahlentheoretische
Funktion
ein (in seinem Artikel ,
in anderer Literatur auch
),
wandelt sie um in
und kommt zu
wobei
den Integrallogarithmus
und
die Möbiusfunktion
bezeichnet. Bezüglich Konvergenz ist zu beachten, dass die Summe
die Nullstellen nach ihrer Konjugation paarweise addiert. Des Weiteren sind die
Terme in der Summe als
zu verstehen (hier bezeichnet
die (komplexe) Integralexponentialfunktion),
denn: Verwechslungen können bei der Auswertung von
über den Hauptzweig des komplexen Logarithmus entstehen!
Numerische Werte der frühen Nullstellen
Die Imaginärteile der „ersten“ Nullstellen sind beispielsweise
| ±k | ±Im ρk | ±k | ±Im ρk |
|---|---|---|---|
| 1 | 14,134725141734693790… | 11 | 52,970321477714460644… |
| 2 | 21,022039638771554993… | 12 | 56,446247697063394804… |
| 3 | 25,010857580145688763… | 13 | 59,347044002602353079… |
| 4 | 30,424876125859513210… | 14 | 60,831778524609809844… |
| 5 | 32,935061587739189690… | 15 | 65,112544048081606660… |
| 6 | 37,586178158825671257… | 16 | 67,079810529494173714… |
| 7 | 40,918719012147495187… | 17 | 69,546401711173979252… |
| 8 | 43,327073280914999519… | 18 | 72,067157674481907582… |
| 9 | 48,005150881167159727… | 19 | 75,704690699083933168… |
| 10 | 49,773832477672302181… | 20 | 77,144840068874805372… |
Über die Eigenschaften dieser Imaginärteile (Irrationalität, Transzendenz, …) ist bis heute nichts bekannt.
Hadamard-Produktentwicklung
Neben dem Euler-Produkt gibt es eine weitere Produktdarstellung der Zeta-Funktion, die erstmals ihre Nullstellen in eine mögliche Definition direkt mit einschließt. Diese ist deshalb so bedeutend, weil sie der Schlüssel für den Zusammenhang zwischen Primzahlen und Nullstellen ist. Der entscheidende Schritt in Bernhard Riemanns Arbeit war nämlich der „Vergleich“ dieser beiden Produkte, was schließlich ein enges Verhältnis zwischen den Produktelementen (in diesem Falle Primzahlen und Nullstellen) impliziert.
Über den Produktsatz von Weierstraß für holomorphe Funktionen ist es möglich, die Zeta-Funktion anhand ihrer Nullstellen über ein Produkt der Form
explizit zu rekonstruieren, wobei
eine meromorphe und nullstellenfreie (meist elementare)
Funktion darstellt. Im Falle der Zeta-Funktion ergibt sich für
die Funktion
und somit unter Verwendung der trivialen sowie nicht-trivialen Nullstellen:
Unter Zuhilfenahme der Produktentwicklung der Gamma-Funktion
erhält man das Hadamard-Produkt,
benannt nach seinem Entdecker Jacques Hadamard, das global in
konvergiert:
Eine etwas einfachere Form des Hadamard-Produktes ist:
Besonders diese letzte Darstellung verdeutlicht, dass sich die -Funktion
im Prinzip komplett aus ihren Nullstellen und ihrer Singularität bei
konstruieren lässt. Dieses Produkt ist jedoch nur bedingt konvergent.
Absolute
Konvergenz ergibt sich, wenn man die Nullstellen „paarweise“ ordnet.
und
sind ein solches Paar. Also:
Aufgrund ihrer langsamen Konvergenzgeschwindigkeit ist die Produktdarstellung jedoch in der Praxis nicht als Grundlage für einen numerischen Berechnungsalgorithmus für die Zeta-Funktion geeignet.
Die riemannsche Vermutung
Die Lage der Nullstellen im kritischen Streifen hängt eng mit Aussagen über
die Verteilung der Primzahlen zusammen. Beispielsweise ist die Aussage, dass auf
dem Rand des kritischen Streifens keine Nullstellen liegen, ein möglicher
Zwischenschritt beim Beweis des Primzahlsatzes.
Weitere Vergrößerungen des „nullstellenfreien Bereiches“ implizieren
Restgliedabschätzungen im Primzahlsatz. Riemann vermutete im Jahr 1859, dass
alle Nullstellen auf der parallel zur imaginären Achse verlaufenden Geraden
liegen. Diese so genannte riemannsche
Vermutung konnte bislang weder bewiesen noch widerlegt werden.
Der Verlauf der Zeta-Funktion in der komplexen Ebene, besonders entlang von
parallel zur imaginären Achse verlaufenden Streifen, wird wegen des
Zusammenhangs mit der Primzahlverteilung und des davon unmittelbar betroffenen
sogenannten Faktorisierungsproblems
seit kurzem auch gezielt mit physikalischen Methoden untersucht, und zwar mit Interferenz-Methoden
analog zur Holographie.
Man teilt dazu die definierende Summe in zwei Teile mit positiver bzw. negativer
Phase auf,
bzw.
,
die man anschließend zur Interferenz bringt.
Zusammenhänge zur Theorie der Automorphen Formen
In der Theorie der für die Zahlentheorie wichtigen Modulformen taucht die riemannsche Zeta-Funktion an einigen Stellen auf.
Zeta-Werte als Koeffizienten von Eisensteinreihen
Für die Gewichte
sind die sog. Eisensteinreihen
Modulformen bezüglich der vollen Modulgruppe .
Als solche besitzen sie auf der oberen Halbebene eine Fourierentwicklung. Diese
ist explizit gegeben durch
Unter Einsatz von Euler's Formel für positive, gerade ganzzahlige Funktionswerte kann jedoch die folgende, für die Zahlentheorie enorm wichtige, Normalisierung vorgenommen werden:
Die zu
zugehörige L-Funktion ist ferner gegeben durch
Dieses Prinzip verallgemeinert sich für Eisensteinreihen zu Kongruenzuntergruppen. Hier hängen die konstanten Koeffizienten mit Werten von L-Funktionen zu Dirichlet-Charakteren zusammen.
Beziehung zu nicht-holomorphen Eisensteinreihen
Für komplexe Zahlen
mit
und
mit
konvergiert die Eisensteinreihe
absolut. Die dadurch definierte Funktion ist nicht-holomorph und zudem (für
fixierte )
invariant in
unter Wirkung der vollen Modulgruppe. Zudem lässt sie sich (für fixierte
)
in
meromorph in die gesamte Ebene fortsetzen mit einfachen Polen in
und
,
es gilt die Funktionalgleichung
Diese Parallele zur Theorie der Zeta-Funktion lässt bereits einen Zusammenhang vermuten. Es gilt die Darstellung
wobei
die Untergruppe der Translationen von
bezeichnet. Betrachtet man zudem die Fourierentwicklung
so gilt
Nicht-holomorphe Eisensteinreihen, und damit auch die Zeta-Funktion selbst, spielen eine fundamentale Rolle bei der sogenannten Ranking-Selberg Methode.
Beziehung zur Thetafunktion
Eine sehr wichtige Eigenschaft der riemannschen Zeta-Funktion ist ihre Funktionalgleichung. Diese drückt sich am einfachsten über
aus und es ist zu bemerken, dass auf der rechten Seite erstaunlicherweise die
komplexe Variable
einfach durch
ersetzt wird.
Es gibt mehrere Herleitungsvarianten zum Auffinden dieser Gleichung. Zwei
verschiedene zeigte bereits Riemann. Eine davon schließt einen einfachen
Spezialfall der jacobischen
Theta-Reihe direkt mit ein, nämlich .
Von Vorteil ist die Modifizierung
,
es gilt
.
Die Theta-Funktion ist dabei eine Modulform halbganzen Gewichts: Mit der poissonschen
Summenformel fand bereits Carl Gustav Jacob Jacobi
die Identität
,
woraus sofort
folgt.
Ausgangspunkt ist die Integraldarstellung
Der folgende Trick ist eine Standard-Umformung beim Beweis des heckeschen
Umkehrsatzes. Durch eine Aufspaltung des Integrals in die Intervalle
und
,
wobei in letzteres die Substitution
vorgenommen wird:,
folgt
Das zweite Integral kann elementar berechnet werden:
Wie man leicht erkennt, ist die rechte Seite unter der Abbildung
unverändert, woraus schon die Funktionalgleichung folgt. Diese Argumentation ist
deshalb gerechtfertigt, da das Integral auf der rechten Seite nun für alle
existiert.
Beukers'
Beweis der Irrationalität von 
1987 konnte Frits Beukers die Irrationalität von
mit Hilfe der Theorie der Modulformen
beweisen. Dafür betrachtete er die Funktion
welche eine Modulform zum Gewicht 4 für die Kongruenzuntergruppe
ist. Die zu diesem
korrespondierende L-Funktion
ist dann
Das Argument bezieht sich letztlich auf eine Technik, welche Konvergenzradien
von Umkehrfunktionen lokal injektiver, meromorpher Funktionen ausnutzt.
Nach heutigem Wissensstand lässt sich der Ansatz von Beukers jedoch nicht auf
die Fälle
übertragen.
Anwendung in der analytischen Zahlentheorie
Im Wesentlichen gibt es zwei Anwendungstypen.
- Typ 1: Man hat eine zahlentheoretische Funktion, d.h. Zahlen
die interessante arithmetische Informationen enthalten. Zum Beispiel könnte
die Anzahl aller ganzen Zahlen
darstellen, die teilerfremd zu
sind. Man will nun das Verhalten der Summe
für größer werdende
untersuchen. Dabei kann eine Möglichkeit sein, die von den
erzeugte Dirichlet-Reihe
zu betrachten. Hat diese gute analytische Eigenschaften, hängt also zum Beispiel stark mit der riemannschen Zeta-Funktion zusammen, kann mit Hilfe von Taubertheorie das Problem angegangen werden. Dabei gilt: je detaillierter die eingehenden Informationen sind, desto bessere Rückschlüsse können gezogen werden. Dies ist ein weiterer Hinweis auf die Bedeutung der riemannschen Vermutung.
Da Taubersätze meistens nicht geeignet sind, Restglieder abzuschätzen, kommen oft auch feinere Methoden zum Einsatz. In diesem Kontext ist zum Beispiel auf die Selberg-Delange Methode verwiesen.
- Typ 2: Hat man umgekehrt gewisse Informationen über die Zahlen
gesammelt, so kann man diese in manchen Fällen auf die erzeugte Dirichlet-Reihe
anwenden, um so Informationen über deren Verhalten zu treffen. In diesem Kontext sei zum Beispiel auf die Mertenssche Vermutung verwiesen, die allerdings bereits widerlegt wurde.
Im Folgenden werden einige wichtige Beispiele gegeben.
Zusammenhang zum Primzahlsatz
Wie bereits der 15-jährige Gauß
vermutete, wächst die Anzahl aller Primzahlen
unter einer gegebenen Schranke
asymptotisch gleich wie der Ausdruck
.
Es gilt also
Dieser sogenannte Primzahlsatz wurde jedoch erst hundert Jahre später unabhängig von Jacques Hadamard und Charles-Jean de La Vallée Poussin bewiesen. Dafür betrachtet man die sog. Mangoldt-Funktion
Der Primzahlsatz ist nun äquivalent zu der Aussage
Dies wurde von Pafnuti Lwowitsch Tschebyschow
gezeigt. Betrachtet man die von
erzeugte Dirichlet-Reihe, ergibt sich
Aus
für alle
folgt, dass die Funktion
auf dem ganzen Streifen
(außer im Punkt
)
holomorph ist, was wegen
den Einsatz eines Taubersatzes
ermöglicht. Damit folgt
und der Primzahlsatz ist bewiesen.
Erstaunlicherweise ist im Beweis des Primzahlsatzes absolut entscheidend,
dass die Zeta-Funktion auf der Geraden
keine Nullstellen besitzt. Bereits hier ist also zu erkennen, dass es einen
Zusammenhang zwischen Primzahlen und den Nullstellen der Zeta-Funktion gibt. In
der Tat, durch die Angabe nullstellenfreier Gebiete lässt sich das Restglied
in
weiter verbessern.
In Verbindung mit zahlentheoretischen Funktionen
Es existieren Zusammenhänge zwischen einigen zahlentheoretischen
Funktionen und der -Funktion.
Diese Verbindungen drücken sich in Dirichlet-Reihen aus, die über die
betreffenden zahlentheoretischen Funktionen gebildet werden. Hierbei macht man
sich zu Nutze, dass das Produkt zweier (oder generell mehrerer) konvergenter
Dirichlet-Reihen eine wiederum konvergente Dirichlet-Reihe ergibt. Man spricht
auch von der sogenannten Dirichlet-Faltung
zweier (oder mehrerer) Dirichlet-Reihen. In diesem Zusammenhang kann man sich
zum Beispiel die Dirichlet-Reihen von
,
oder auch
ansehen.
Teilerfunktionen
Man findet beispielsweise die Relation:
wobei
die Teileranzahlfunktion
darstellt, die zählt, wie viele natürliche Teiler
eine Zahl
besitzt. Zu diesem Ergebnis gelangt man durch systematisches Ausmultiplizieren
des Quadrates der Dirichlet-Reihe der Zeta-Funktion. Da es sich dabei um das
Produkt zweier (konvergenter) Dirichlet-Reihen handelt, kann es, wie oben
beschrieben, wiederum über eine Dirichlet-Reihe dargestellt werden.
Die aus dieser Faltung erzeugte Dirichlet-Reihe hat nun eine neue
zahlentheoretische Funktion, die als
bezeichnet wird. Der Summenindex wird als
gewählt, um Verwechslungen zu vermeiden. Der vorletzte Schritt der Auswertung
zeigt nun, dass man den Wert von
über die Anzahl aller natürlichen Zahlenpaare
gewinnen kann, für die
gilt. Somit reduziert sich die Frage nach dem Wert von
darauf, wie viele Teiler die betroffene Zahl
besitzt.
Allgemeiner hat man:
wobei
die verallgemeinerte Teilerfunktion
ist.
Möbiusfunktion
Mit der Möbiusfunktion
erhält man eine Dirichlet-Reihe, die den Kehrwert der -Funktion
erzeugt. Es gilt dann:
Zur Erklärung dieses Zusammenhangs betrachtet man
also einfach den Kehrwert des Euler-Produkts, und bildet durch konsequentes Ausmultiplizieren die dazugehörige Dirichlet-Reihe, die sich dann definitionsgemäß über die Möbiusfunktion erstreckt.
Eulersche Phi-Funktion
Die Dirichlet erzeugende Funktion für die Eulersche -Funktion
ist gegeben durch
Damit folgt unter anderem
Summe von Quadraten
Die Dirichlet-Reihe der Quadratsummen-Funktion
,
die angibt, auf wie viele Arten eine natürliche Zahl
als Summe von
Quadraten ganzer Zahlen geschrieben werden kann, lässt sich ebenfalls auf die
riemannsche Zetafunktion überleiten. So erhält man beispielsweise zusammen mit
der dirichletschen
Betafunktion:
Insbesondere lässt sich über diesen Ansatz zeigen, dass sich der Limes
einer festen Konstanten
nähert. Diese Sierpiński-Konstante
(benannt nach Wacław Sierpiński) lässt sich in Abhängigkeit von der Kreiszahl, der
Euler-Mascheroni Konstante und logarithmierten Werten der Gammafunktion auch
schreiben als:
Mittels eines Taubersatzes findet man außerdem
was jedoch auch mittels elementarer Geometrie (durch Zählen von Gitterpunkten in Kreisen mit dem Ursprung als Mittelpunkt) gezeigt werden kann!
Ähnliche Ausdrücke finden sich für 4 bzw. 8 Quadrate:
.
Daraus folgt unter anderem unmittelbar der Satz von Jacobi.
Anwendung in der algebraischen Zahlentheorie und Verallgemeinerungen
Dirichletsche L-Funktionen
Die riemannsche Zeta-Funktion ist eine spezielle dirichletsche L-Funktion.
Sie korrespondiert zum sog. trivialen Charakter
für alle Werte
.
Aus diesem Grunde ist sie zentraler Gegenstand der algebraischen Zahlentheorie,
die sich mit der Struktur von Charakteren zu gewissen Gruppen befasst.
Verwandtschaft zur dedekindschen Zeta-Funktion von Zahlkörpern
Beziehung zum Zahlkörper 
Im Falle
ist die dedekindsche Zeta-Funktion
gerade die riemannsche Zeta-Funktion. Insbesondere hängt diese mit den
Primelementen in deren Ganzheitsring
zusammen.
Beziehung zu quadratischen Zahlkörpern
Ist
eine quadratische Erweiterung von
mit Diskriminante
,
so hängt ihre dedekindsche Zeta-Funktion eng mit der riemannschen Zeta-Funktion
zusammen. Es gibt dann nämlich einen Dirichlet-Charakter
modulo
,
so dass
wobei
die zu
gehörige dirichletsche L-Funktion bezeichnet. Die Funktion
hat einen Pol erster Ordnung in
und erfüllt eine Funktionalgleichung.
Verwendet werden kann die dedekindsche Zetafunktion unter anderem zur
Berechnung der Klassenzahl
von .
Dafür wird die sogenannte Klassenzahlformel
verwendet.
Ein wichtiger Spezialfall ist .
Die dazu korrespondierende Zeta-Funktion ist gegeben durch
wobei die dirichletsche
Betafunktion
zum Charakter
modulo 4 korrespondiert. Daraus ergeben sich relativ direkt Formeln für die
Summe von zwei Quadraten.
Abelsche Erweiterungen
Im Falle, dass
eine abelsche
Erweiterung ist, ist der Quotient
eine ganze
Funktion. D.h. gewissermaßen, dass die riemannsche Zeta-Funktion in diesem
Falle ein "Teiler von
"
ist. Dass dies auch für nicht-abelsche Erweiterungen richtig ist, ist Gegenstand
tiefer zahlentheoretischer Vermutungen (Artinsche
Vermutung).
Beziehungen zu anderen speziellen Funktionen
Als Taylor-Koeffizienten von Kotangens und Digamma-Funktion
In der Analysis tritt die Zeta-Funktion unter anderem als Koeffizientenfolge in den Taylor-Reihen des Kotangens und der Digamma-Funktion auf.
Die erzeugende
Funktion der Folge
mit
für alle
ist:
wobei
hier die Digamma-Funktion und
die Euler-Mascheroni-Konstante
bezeichnet.
Summiert man außerdem in einer Potenzreihe, die die Zetafunktionswerte als Koeffizienten hat, nur über die geradzahligen Exponenten bzw. Folgeglieder, so ergibt sich:
ebenfalls mit Konvergenzradius 1.
Diese Identität bietet einen Beweisansatz für Euler's Formel für .
Beziehung zur Polygammafunktion
Espinosa und Moll haben 2003 die Relation
mit der Digammafunktion
und der auf komplexe Ordnungen
verallgemeinerten
Polygammafunktion
aufgezeigt.
Unter Ausnutzung der Beziehung
zur hurwitzschen Zeta-Funktion und Einsetzen in die allgemeinere Relation
gelangt man zu
Damit sind die Nullstellen der ζ-Funktion Lösungen ρ der Gleichung
Wegen der „Multiplikationsformel“
lässt sich für ,
sogar die allgemeinere Beziehung
herleiten.
Beziehung zur Primzetafunktion
Es gilt für alle
mit
:
wobei
mit
die Primzetafunktion bezeichnet. Mit Hilfe von Möbius-Inversion lässt sich daraus eine Möglichkeit ableiten, die Primzetafunktion schnell aus einer Reihe über logarithmierte Zeta-Funktionen zu gewinnen.
Diese kuriose Formel kann dazu verwendet werden, die Primzetafunktion extrem effizient zu berechnen. Zum Beispiel fand Henri Cohen innerhalb weniger Millisekunden
Ferner ist es möglich zu zeigen, dass die Reihe
der reziproken Primzahlen divergiert.
Sonstiges Auftreten
In der Analysis
Es gibt eine reichhaltige Fülle an unendlichen Reihen mit besonderen Grenzwerten, die die Zeta-Funktion beinhalten. Zwei Beispiele für Reihen mit rationalen Grenzwerten sind:
und
Zusammen mit der Euler-Mascheroni-Konstante
hat man:
und auch:
Auch für die catalansche
Konstante
existieren solche Reihen:
In der Wahrscheinlichkeitstheorie
Die Zeta-Funktion spielt eine zentrale Rolle bei der sogenannten Zipf-Verteilung. Es
gilt für eine Zufallsvariable
:
Auch einige Wahrscheinlichkeitsgesetze aus der Zahlentheorie stehen in engem Zusammenhang zu der Zeta-Funktion. Die Wahrscheinlichkeit, dass eine zufällig gewählte Zahl quadratfrei ist, und ebenso die Wahrscheinlichkeit, dass zwei zufällig gewählte Zahlen teilerfremd sind, ist gleich
(Folge A059956 in OEIS).
Allgemeiner ist
die Wahrscheinlichkeit, dass n positive ganze Zahlen keine k-te
Potenz größer 1 als gemeinsamen Teiler haben.
Als Funktionswert spezieller Funktionen
Die riemannsche Zeta-Funktion taucht ebenfalls bei der Auswertung bestimmter Funktionswerte anderer spezieller Funktionen auf, was nicht zuletzt durch ihre Verbindung zur Gamma-Funktion (beispielsweise in der Funktionalgleichung) begründet werden kann. Zum Beispiel ergibt sich mit der Polygamma-Funktion:
Numerische Berechnung
Für eine schnelle numerische Berechnung der Funktion
sind viele klassische Darstellungsformen eher unbrauchbar. Dazu zählen in etwa
im Besonderen die Dirichlet-Reihe, das Euler-Produkt, die Mellin-Transformation
und das Hadamard-Produkt. Für effiziente Leistung ist ein endlicher
approximativer Summenausdruck mit hoher Konvergenzgeschwindigkeit
am geeignetsten.
Als gute Methode erweist sich die „abgebrochene“ Summenformel, die mit Hilfe der Euler-MacLaurin-Summenformel,
gewonnen wird, wobei f als Mindestvoraussetzung eine auf dem Intervall
q-mal differenzierbare
Funktion ist,
die Bernoulli-Polynome
sind und
den ganzzahligen Anteil von
darstellt.
Setzt man hier
ergibt sich beispielsweise die in der Literatur häufig zitierte Darstellung
die für
gültig ist.
Hierfür wird zunächst eine beliebige natürliche Zahl
festgelegt, für die außerdem
gelten sollte. Es gilt dann:
wobei das Restglied
durch
gegeben ist. Bei der (freien) Wahl von
ist zu beachten, dass das Restglied nur auf der Halbebene
konvergiert. Daher muss stets
gelten. Für größer werdende Werte von
verkleinert sich der Fehler
unabhängig von
rapide.
Durch Anwendung der Funktionalgleichung (eine schnelle Berechnung der
Gamma-Funktion und der Exponentialfunktion
ist leicht zu implementieren), kann zudem ohne Einschränkung
angenommen werden. Hier ist die Summenformel deutlich schneller.
Die Nützlichkeit dieser Approximation ist bereits länger bekannt.
Beispielsweise ermittelte Leonhard Euler 1735 den Wert von
auf etwa 20 Stellen genau, bevor er das Basler Problem, das sich mit dem
analytisch „exakten“ Wert von
befasste, löste. Diese numerische Auswertung war für ihn die praktische
Bestätigung für die Richtigkeit seines exakt ermittelten Wertes.
Weiter fand der dänische Mathematiker Jørgen Pedersen Gram im Jahr 1903 numerische Werte der ersten 15 nicht-trivialen Nullstellen, wobei er die ersten zehn Nullstellen auf sechs und die weiteren fünf auf jeweils eine Stelle nach dem Komma ermittelte.
Beispiele
Als ein Beispiel bietet sich die numerische Annäherung des Zahlenwertes von
an. Für eine sehr gute Approximation reichen die Werte
und
vollkommen aus. Einsetzen ergibt:
Die folgende Tabelle zeigt die numerische Auswertung dieser Rechnung.
| Term | Numerischer Wert |
|---|---|
Diese mit wenig Aufwand gewonnene Approximation stimmt mit dem tatsächlichen Wert
bereits in sechs Dezimalstellen (gerundet) nach dem Komma überein.
Zur Unterstreichung der Effektivität sei bemerkt: hätte Euler stattdessen die
Formel
benutzt, so wären für die gleiche Approximation ca. 1.000.000 Summanden nötig
gewesen. Geht man davon aus, dass Euler per Hand pro Term durchschnittlich 20
Sekunden Rechenzeit benötigte, wären dies ca. zwei Drittel Jahre
ununterbrochenes Rechnen gewesen.
Analog kann der Dezimalwert von
angenähert werden. Hier reicht die Wahl von
und
.
| Term | Numerischer Wert |
|---|---|
Auch dieser Wert stimmt auf sechs Dezimalstellen genau.
Andere Ausdrücke für die ζ-Funktion
Neben ihrer elementaren Reihendarstellung besitzt die Zeta-Funktion eine reiche Fülle an weiteren Ausdrücken, von denen einige im Folgenden aufgeführt werden. Hierbei sei jedoch zu bemerken, dass sich die allermeisten dieser Formeln für eine effiziente numerische Berechnung eigentlich nicht eignen. Viele dieser Ausdrücke spielen jedoch in der reinen Mathematik eine Rolle.
Erwähnenswert ist der interessante Ausdruck
,
der für
(also wiederum auch im kritischen Streifen) konvergiert.
Ein interessanter und exotischer Ausdruck ergibt sich, wenn man direkt die elementare Reihendarstellung der Zeta-Funktion in die Abel-Plana-Summenformel einsetzt:
Fasst man dabei die beiden Terme auf der rechten Seite zusammen, erhält man
,
wobei das Integral allerdings einschränkend nur für
konvergiert.
Eine erwähnenswerte Formel für die Ableitung der -Funktion
lässt sich mittels logarithmischer
Ableitung gewinnen, also über die Identität:
Setzt man hier
für die
-te
Primzahl (Euler-Produkt), ergibt sich:
Verallgemeinerungen und andere Zeta-Funktionen
In dem Wunsch, die Definition der riemannschen Zeta-Funktion zu verallgemeinern oder zu variieren, wurden zahlreiche verwandte Funktionen eingeführt und untersucht. Häufig tragen diese ebenfalls den Namen „Zeta-Funktion“, verbunden mit dem Namen ihres „Entdeckers“. Insbesondere seien hier die dedekindsche Zeta-Funktion, die hurwitzsche Zeta-Funktion und die lerchsche Zeta-Funktion genannt, siehe auch Liste aller Zeta-Funktionen. Dabei verallgemeinert die dedekindsche Zeta-Funktion die riemannsche vom Körper der rationalen Zahlen auf beliebige algebraische Zahlkörper. Mit Hilfe der hurwitzschen Zeta-Funktion lassen sich die riemannsche Zeta-Funktion und die dirichletschen L-Funktionen einheitlich behandeln. Die weit reichende Definition der lerchschen Zeta-Funktion gestattet nicht nur Spezialisierungen zur hurwitzschen und somit auch zur riemannschen Zeta-Funktion, sondern beinhaltet noch zahlreiche weitere, wichtige Funktionen als Spezialfälle. Ähnlich definierte „verallgemeinerte Zeta-Funktionen“ werden auch in der theoretischen Physik verwendet, und zwar im Zusammenhang mit der systematischen sogenannten semiklassischen Näherung quantenmechanischer Resultate.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 30.12. 2021