Konvergenzradius

Der Konvergenzradius ist in der Analysis eine Eigenschaft einer Potenzreihe der Form

$f(x)=\sum _{{n=0}}^{\infty }a_{n}(x-x_{0})^{n}$ ,

die angibt, in welchem Bereich der reellen Gerade oder der komplexen Ebene für die Potenzreihe Konvergenz garantiert ist.

Definition

Der Konvergenzradius ist als das Supremum aller Zahlen $\rho \geq 0$ definiert, für welche die Potenzreihe für (mindestens) ein mit $|x-x_{0}|=\rho$ konvergiert:

$r:=\sup \left\{|x-x_{{0}}|\ \left|\ \sum _{{n=0}}^{{\infty }}a_{{n}}(x-x_{{0}})^{{n}}\ {\text{konvergiert}}\right.\right\}$

Falls die Potenzreihe für alle reellen Zahlen bzw. auf der ganzen komplexen Zahlenebene konvergiert, also diese Menge der $\rho$ (nach oben) unbeschränkt ist, sagt man, der Konvergenzradius ist unendlich: $r = \infty$ .

Folgerungen aus dem Konvergenzradius

Für eine Potenzreihe mit Konvergenzradius gilt:

Ist $|x-x_{0}|<r$ , so ist die Potenzreihe absolut konvergent.
Ist $|x-x_{0}|>r$ , so ist die Potenzreihe divergent.
Ist $|x-x_{0}|=r$ , so kann keine allgemeine Aussage getroffen werden, in manchen Situationen hilft aber der Abelsche Grenzwertsatz.

Wird eine reelle Potenzreihe betrachtet, deren Koeffizienten $a_{n}$ reelle Zahlen sind, und sind auch $x,~x_{0}$ reell, so ist der Konvergenzbereich nach Auflösung der Betragsungleichungen das Intervall $(x_{0}-r,~x_{0}+r)$ sowie möglicherweise einer der oder beide Randpunkte. Für Potenzreihen im Komplexen, das heißt, alle diese Größen können komplexe Zahlen sein, besteht der Konvergenzbereich dieser Funktionenreihe aus dem Inneren der Kreisscheibe um den Mittelpunkt $x_{0}$ und mit Radius , dem Konvergenzkreis, sowie möglicherweise aus einigen seiner Randpunkte.

Außerdem gilt für alle $r^{{\prime }}<r$ , dass die Potenzreihe gleichmäßig für alle mit $|x-x_{0}|\leq r^{{\prime }}$ konvergiert. Auf einem inneren Kreis oder Teilintervall liegt also auch stets eine gleichmäßige Konvergenz vor.

Bestimmung des Konvergenzradius

Der Konvergenzradius lässt sich mit der Formel von Cauchy-Hadamard berechnen: Es gilt

$r={\frac {1}{\limsup \limits _{{n\rightarrow \infty }}\left({\sqrt[ {n}]{|a_{n}|}}\right)}}.$

Dabei gilt r = 0 , falls der Limes superior im Nenner gleich $+\infty$ ist, und $r=+\infty$ , falls er gleich $0$ ist.

Wenn ab einem bestimmten Index alle $a_{n}$ von 0 verschieden sind und der folgende Limes existiert, dann kann der Konvergenzradius einfacher durch

$r=\lim _{{n\rightarrow \infty }}{\bigg |}{\frac {a_{{n}}}{a_{{n+1}}}}{\bigg |}$

berechnet werden. Diese Formel ist aber nicht immer anwendbar, zum Beispiel bei der Koeffizientenfolge $a_{{2n}}=1,~a_{{2n+1}}=1/n$ : Die zugehörige Reihe hat den Konvergenzradius 1, aber der angegebene Limes existiert nicht. Die Formel von Cauchy-Hadamard ist dagegen immer anwendbar.

Beispiele für unterschiedliches Randverhalten

Die folgenden drei Beispiele reeller Potenzreihen haben jeweils Konvergenzradius 1, konvergieren also für alle im Intervall (-1,1) ; das Verhalten an den Randpunkten ist jedoch unterschiedlich:

$\sum _{{n=0}}^{\infty }x^{n}$ konvergiert an keinem der Randpunkte $\pm 1$ .
$\sum _{{n=1}}^{\infty }{\frac {x^{n}}{n^{2}}}$ konvergiert an beiden Randpunkten und .
$\sum _{{n=1}}^{\infty }{\frac {x^{n}}{n}}$ konvergiert nicht am rechten Randpunkt (harmonische Reihe), wohl aber am linken Randpunkt (alternierende harmonische Reihe).

Einfluss des Entwicklungspunktes auf den Konvergenzradius

Die drei Konvergenzkreise der Funktion

in Abhängigkeit vom Entwicklungspunkt. Sie schneiden sich im Punkt

da hier die Funktion eine Singularität besitzt

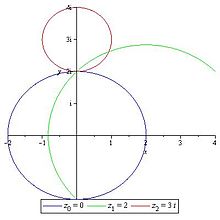
Der Entwicklungspunkt $z_{0}$ einer Potenzreihe hat einen direkten Einfluss auf die Koeffizientenfolge $(a_{n})_{{n\in \mathbb{N} }}$ und damit auch auf den Konvergenzradius. Betrachtet man beispielsweise die Analytische Funktion

$f(z)={\frac {1}{2i-z}}$

in ihrer Potenzreihendarstellung

$f(z)={\frac {1}{2i}}\cdot {\frac {1}{1-({\frac {z}{2i}})}}={\frac {1}{2i}}\cdot \sum _{{n=0}}^{\infty }\left({\frac {z}{2i}}\right)^{n}$ .

Diese Umformungen folgen direkt mittels der geometrischen Reihe. Diese Darstellung entspricht der Potenzreihe um den Entwicklungspunkt z_0=0 und mit dem Wurzelkriterium folgt für den Konvergenzradius $r_{0}=2$ .

Wählt man dagegen $z_{1}=2$ als Entwicklungspunkt, so folgt mit einigen algebraischen Umformungen

$f(z)={\frac {1}{-(z-2)-2+2i}}=-{\frac {1}{2i-2}}\cdot {\frac {1}{1-({\frac {z-2}{2i-2}})}}={\frac {1}{2i-2}}\cdot \sum _{{n=0}}^{\infty }\left({\frac {z-2}{2i-2}}\right)^{n}$ .

Auch hier folgt mittels des Wurzelkriteriums der Konvergenzradius $r_{1}={\sqrt {8}}$ .

Ein dritter Entwicklungspunkt $z_{2}=3i$ liefert mit analogem Vorgehen

$f(z)={\frac {1}{-(z-3i)-3i+2i}}={\frac {1}{-i}}\cdot {\frac {1}{1-({\frac {z-3i}{i}})}}={\frac {1}{-i}}\cdot \sum _{{n=0}}^{\infty }\left({\frac {z-3i}{i}}\right)^{n}$

als Potenzreihendarstellung mit dem Konvergenzradius $r_{2}=1$ . Zeichnet man diese drei Konvergenzradien um ihre Entwicklungspunkte, so schneiden sie sich alle im Punkt z'=2i da hier die Funktion f eine Singularität besitzt und nicht definiert ist. Anschaulich dehnt sich also der Konvergenzkreis um einen Entwicklungspunkt aus, bis er an eine nicht definierte Stelle der Funktion stößt.

Herleitung

Die Formeln für den Konvergenzradius lassen sich aus den Konvergenzkriterien für Reihen herleiten.

Wurzelkriterium

Die Formel von Cauchy-Hadamard ergibt sich aus dem Wurzelkriterium. Nach diesem Kriterium konvergiert die Potenzreihe

$\sum \limits _{{n=0}}^{{\infty }}{a_{n}}\left(x-x_{0}\right)^{n},$

absolut wenn

${\underset {n\to \infty }{{\mathop {\lim \sup }}}}\,{\sqrt[ {n}]{\left|a_{n}\left(x-x_{0}\right)^{n}\right|}}=\left|x-x_{0}\right|{\underset {n\to \infty }{{\mathop {\lim \sup }}}}\,{\sqrt[ {n}]{|a_{n}|}}<1.$

Auflösen nach $\left|x-x_{0}\right|$ liefert den Konvergenzradius

$\left|x-x_{{0}}\right|<{\frac {1}{{\underset {n\to \infty }{{\mathop {\lim \sup }}}}{\sqrt[ {n}]{|a_{{n}}|}}}}=\liminf _{{n\rightarrow \infty }}\,|a_{{n}}|^{{-1/n}}=r.$

Quotientenkriterium

Sofern fast alle $a_{n}$ ungleich Null sind, konvergiert die Potenzreihe $\sum \limits _{{n=0}}^{{\infty }}{a_{n}}\left(x-x_{0}\right)^{n}$ nach dem Quotientenkriterium, wenn folgende Bedingung erfüllt ist:

$\limsup _{{n\rightarrow \infty }}\left|{\frac {a_{{n+1}}\left(x-x_{0}\right)^{{n+1}}}{a_{n}\left(x-x_{0}\right)^{n}}}\right|=\limsup _{{n\rightarrow \infty }}\left|{\frac {a_{{n+1}}}{a_{n}}}\left(x-x_{0}\right)\right|=\left|x-x_{0}\right|\limsup _{{n\rightarrow \infty }}\left|{\frac {a_{{n+1}}}{a_{n}}}\right|<1.$

Auflösen nach $\left|x-x_{0}\right|$ liefert:

$\left|x-x_{{0}}\right|<{\frac {1}{{\underset {n\to \infty }{{\mathop {\lim \sup }}}}\left|{\frac {a_{{n+1}}}{a_{{n}}}}\right|}}=\liminf _{{n\rightarrow \infty }}\left|{\frac {a_{{n}}}{a_{{n+1}}}}\right|=:r.$

Die Potenzreihe konvergiert also für $\left|x-x_{0}\right|<r$ . Dies ist im Allgemeinen aber nicht der Konvergenzradius. Das liegt daran, dass das Quotientenkriterium im folgenden Sinne echt schwächer ist als das Wurzelkriterium: Ist

${\underset {n\to \infty }{{\mathop {\lim \sup }}}}\left|{\frac {b_{{n+1}}}{b_{{n}}}}\right|>1$ ,

so kann im Allgemeinen nicht darauf geschlossen werden, dass die Reihe $\sum \limits _{{n=0}}^{\infty }{b_{n}}$ divergiert. Die Divergenz erhält man aber aus

${\underset {n\to \infty }{{\mathop {\liminf }}}}\left|{\frac {b_{{n+1}}}{b_{{n}}}}\right|>1$ .

Ähnlich wie oben schließt man also, dass die Potenzreihe $\sum \limits _{{n=0}}^{{\infty }}{a_{n}}\left(x-x_{0}\right)^{n}$ für $\left|x-x_{0}\right|>R$ divergiert, wobei

$R:={\frac {1}{\liminf _{{n\to \infty }}{\left|{\frac {a_{{n+1}}}{a_{n}}}\right|}}}$ .

Man kann im Allgemeinen folglich nur aussagen, dass der Konvergenzradius zwischen und liegt.

Daraus folgt aber insbesondere: Aus der Existenz von $\lim _{{n\to \infty }}|a_{{n+1}}/a_{n}|$ folgt r=R und in diesem besonderen Falle ist

$r=R={\frac {1}{\lim \limits _{{n\to \infty }}|a_{{n+1}}/a_{n}|}}=\lim \limits _{{n\to \infty }}\left|{\frac {a_{n}}{a_{{n+1}}}}\right|$

der gesuchte Konvergenzradius.

Basierend auf einem Artikel in:

Wikipedia.de