Beschränktheit

Eine beschränkte Menge mit oberen und unteren Schranken.

Eine nach oben beschränkte Menge mit Supremum.

Die Eigenschaft der Beschränktheit wird in verschiedenen Bereichen der Mathematik einer Menge zugeordnet. Die Menge wird dann als (nach unten oder oben) beschränkte Menge bezeichnet. Damit ist zunächst gemeint, dass alle Elemente der Menge bezüglich einer Ordnungsrelation $\leq$ nicht unterhalb bzw. nicht oberhalb einer bestimmten Schranke liegen. Genauer spricht man dann davon, dass die Menge bezüglich der Relation $\leq$ (nach unten oder oben) beschränkt ist. Die Begriffe obere und untere Schranke werden im Artikel Supremum ausführlich beschrieben.

Viel häufiger wird der Begriff in einem übertragenen Sinn gebraucht. Dann heißt eine Menge (nach oben) beschränkt, wenn eine Abstandsfunktion zwischen ihren Elementen, die als Wertevorrat meist die nichtnegativen reellen Zahlen hat, nur Werte nicht oberhalb einer bestimmten reellen Zahl annimmt. Hier versteht sich die Beschränktheit nach unten (nämlich durch 0) meist von selbst, daher wird hier einfach nur von einer beschränkten Menge gesprochen. Genauer müsste man sagen: Die Menge ist bezüglich der Abstandsfunktion (und der natürlichen Anordnung von deren Wertevorrat) beschränkt.

Daneben gibt es den Begriff einer (nach oben oder unten) beschränkten Funktion. Darunter ist eine Funktion zu verstehen, deren Bildmenge (als Teilmenge einer halbgeordneten Menge) die entsprechende Eigenschaft hat oder im übertragenen Sinn: Die Menge der Bilder der Funktion hat bezüglich einer Abstandsfunktion die entsprechende Beschränktheitseigenschaft.

Definitionen

Beschränktheit bezüglich einer Ordnungsrelation

Sei eine durch die Relation $\leq$ halbgeordnete Menge und eine Teilmenge von .

Ein Element $b \in M$ heißt obere Schranke von , wenn gilt: $\forall x \in S : x\leq b$ . Das bedeutet: Alle Elemente von sind kleiner oder gleich der oberen Schranke . Falls eine solche obere Schranke existiert, heißt nach oben beschränkt (bezüglich der Relation $\leq$ ).
Ein Element $a \in M$ heißt untere Schranke von , wenn gilt: $\forall x \in S : a\leq x$ . Das bedeutet: Alle Elemente von sind größer oder gleich der unteren Schranke . Falls eine solche untere Schranke existiert, heißt nach unten beschränkt (bezüglich der Relation $\leq$ ).
Eine Menge , die in diesem Sinn sowohl nach oben als auch nach unten beschränkt ist, wird als beschränkte Menge (bezüglich der Relation $\leq$ ) bezeichnet.
Eine Menge, die nicht beschränkt ist, heißt unbeschränkt.
Eine Funktion $f: X\rightarrow M$ in eine halbgeordnete Menge heißt nach oben bzw. unten beschränkt, wenn in eine obere bzw. untere Schranke für die Bildmenge $S=f(X)=\{f(x)|x\in X\}$ existiert. Ist sowohl nach oben als auch nach unten beschränkt, nennt man beschränkt, sonst unbeschränkt.

Übertragung auf Mengen, auf denen eine Abstandsfunktion definiert ist

Die Begriffe beschränkt und unbeschränkt, die so für eine halbgeordnete Menge definiert sind, werden nun im übertragenen Sinn auch für Mengen mit einer Abstandsfunktion verwendet, wenn die Werte, die diese Funktion annimmt, in der geordneten Bildmenge (meistens nichtnegative reelle Zahlen) die entsprechenden Schranken hat (bzw. nicht hat).

Übertragung auf Funktionen, auf deren Wertevorrat eine Abstandsfunktion definiert ist

Sei eine Menge und $d: X\times X \rightarrow \mathbb{R}$ eine Abstandsfunktion auf , eine beliebige Menge. Eine Funktion $f: N\rightarrow X$ heißt beschränkt (bezüglich der Abstandsfunktion ), wenn die Menge $\left\{d(f(n_1),f(n_2))|n_1,n_2\in N\right\}$ in $\mathbb{R}$ beschränkt ist, sonst unbeschränkt.

Analysis

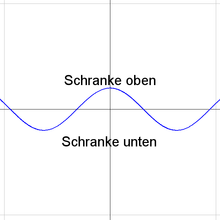
Die Bildmenge der abgebildeten Funktion ist beschränkt, damit ist auch die Funktion beschränkt.

In der Analysis heißt eine Teilmenge der reellen Zahlen nach oben beschränkt, genau dann wenn es eine reelle Zahl mit $k \geq s$ für alle aus gibt. Jede solche Zahl heißt obere Schranke von . Die Begriffe nach unten beschränkt und untere Schranke sind analog definiert.

Die Menge heißt beschränkt, wenn sie nach oben beschränkt und nach unten beschränkt ist. Folglich ist eine Menge beschränkt, wenn sie in einem endlichen Intervall liegt.

Daraus ergibt sich der Zusammenhang: Eine Teilmenge der reellen Zahlen ist genau dann beschränkt, wenn es eine reelle Zahl gibt, so dass |x| < R für alle aus gilt. Man sagt dann, läge in der offenen Kugel (d.h. einem offenen Intervall) um 0 mit Radius .

Im Falle ihrer Existenz nennt man die kleinste obere Schranke das Supremum von , die größte untere Schranke das Infimum.

Eine Funktion $f : X \to \R$ heißt beschränkt auf , wenn ihre Bildmenge f(X) eine beschränkte Teilmenge von $\mathbb R$ ist.

Eine Teilmenge der komplexen Zahlen heißt beschränkt, wenn die Beträge jedes Elementes von eine bestimmte Schranke nicht überschreiten. Das heißt, die Menge ist in der abgeschlossenen Kreisscheibe $K_R(0)=\{z\in\mathbb{C}| |z|\leq R\}$ enthalten. Eine komplexwertige Funktion heißt beschränkt, wenn ihre Bildmenge beschränkt ist.

Ganz entsprechend wird der Begriff in den -dimensionalen Vektorräumen $\mathbb{R}^n$ bzw. $\mathbb{C}^n$ definiert: Eine Teilmenge dieser Räume heißt beschränkt, wenn die Norm ihrer Elemente eine gemeinsame Schranke nicht überschreitet. Diese Definition ist unabhängig von der speziellen Norm, da alle Normen in endlichdimensionalen normierten Räumen zum gleichen Beschränktheitsbegriff führen.

Metrische Räume

Beschränkte Menge (oben) und unbeschränkte Menge (unten)

Eine Menge S aus einem metrischen Raum (M, d) heißt beschränkt, wenn sie in einer Kugel mit endlichem Radius enthalten ist, d.h. wenn ein x aus M und r > 0 existieren, so dass für alle s aus S gilt: $d(x, s) \leq r$ .

Funktionalanalysis

Beschränkte Mengen in topologischen Vektorräumen

Eine Teilmenge eines topologischen Vektorraums heißt beschränkt, wenn es zu jeder Umgebung von 0 ein k>0 gibt, so dass $S\subseteq kU$ gilt.

Ist E ein lokalkonvexer Raum, so ist dessen Topologie durch eine Menge $\mathcal P$ von Halbnormen gegeben. Die Beschränktheit lässt sich dann wie folgt durch Halbnormen charakterisieren: $S\subset E$ ist genau dann beschränkt, wenn $\sup_{x\in S}p(x) < \infty$ für alle Halbnormen $p\in {\mathcal P}$ .

Beispiele beschränkter Mengen

Kompakte Mengen sind beschränkt.
Die Einheitskugel in einem unendlich-dimensionalen normierten Raum ist beschränkt aber nicht kompakt.
Sei $c_{00}$ der Vektorraum aller endlichen Folgen, d.h. aller Folgen , so dass $x_n\in {\mathbb R}, x_n = 0$ für fast alle n. Sei weiter $S:=\{(x_n)_n\in c_{00}; |x_n|\le 1 \, \forall n\}$ . Dann ist S bzgl. der durch $\|(x_n)_n\|_\infty = \sup_{n\in{\mathbb N}}|x_n|$ definierten Norm beschränkt, nicht aber bzgl. der durch $\|(x_n)_n\|_1 = \sum_{n\in {\mathbb N}}|x_n|$ definierten Norm.
Betrachtet man auf dem Raum $c_{00}$ der endlichen Folgen des vorangegangenen Beispiels die durch die Halbnormen definierte lokalkonvexe Topologie, so ist $S:=\{(x_n)_n \in c_{00}; |x_n|\le n \, \forall n\}$ beschränkt. Diese Menge ist für keine der beiden genannten Normen beschränkt.

Permanenzeigenschaften

Teilmengen beschränkter Mengen sind beschränkt.
Endliche Vereinigungen beschränkter Mengen sind beschränkt.
Der topologische Abschluss einer beschränkten Menge ist beschränkt.
Sind S und T beschränkt, so auch $S+T := \{s+t; s\in S, t\in T\}.$
Eine stetige, lineare Abbildung zwischen lokalkonvexen Räumen bildet beschränkte Mengen auf beschränkte Mengen ab (siehe dazu auch: Bornologischer Raum).
Ist E lokalkonvex, so sind die konvexe Hülle und die absolutkonvexe Hülle einer beschränkten Menge wieder beschränkt.

Beschränkte Abbildungen

Sind und topologische Vektorräume, so heißt eine Abbildung $T\colon V\to W$ beschränkt, wenn das Bild jeder beschränkten Teilmenge beschränkt ist.

Sind und normierte Räume, so ist diese Bedingung äquivalent dazu, dass eine Konstante c>0 existiert, so dass

$\|Tx\|\leq c\cdot\|x\|$ für alle $x\in V$

gilt. Die Menge dieser ist nach unten beschränkt und nach oben unbeschränkt, daher existiert das Infimum dieser Menge – es ist identisch mit der Operatornorm von . Man kann zeigen, dass jeder beschränkte lineare Operator zwischen normierten Räumen stetig ist und umgekehrt.

Beschränkte Funktionen und gleichmäßige Beschränktheit

Gleichmäßige Beschränktheit

Der Begriff gleichmäßige Beschränktheit wird nur auf Mengen von Funktionen $f\colon X\rightarrow M$ angewandt, also Mengen von Funktionen mit derselben Definitionsmenge und demselben Wertevorrat . Meist spricht man dann von Familien von Funktionen oder, falls die Familie abzählbar unendlich ist, von einer Funktionenfolge.

Sei eine beliebige Menge. Dann heißt eine Familie $\mathcal{F}$ von auf definierten, reellwertigen Funktionen gleichmäßig beschränkt, wenn es eine reelle Zahl gibt, für die gilt: $\forall x\in X\;\forall f\in \mathcal{F}\colon |f(x)|\leq S$ . Das heißt, ist eine gemeinsame obere Schranke für die Werte der Beträge aller Funktionen aus $\mathcal{F}$ .

Offensichtlich kann eine Familie von Funktionen höchstens dann gleichmäßig beschränkt sein, wenn jede einzelne Funktion der Familie beschränkt ist. Für jede einzelne Funktion $f\in\mathcal{F}$ existiert daher die Supremumsnorm $\|f\|_{\infty}=\sup\{|f(x)| : x\in X\}$ . Eine Familie von Funktionen ist nun genau dann gleichmäßig beschränkt, wenn sie als Menge von Funktionen bezüglich der Supremumsnorm beschränkt ist.

Dies wird auf vektorwertige Funktionen verallgemeinert: Dabei ist eine beliebige Menge, ein reeller oder komplexer normierter Raum mit der Norm $\|\cdot\|_V \colon V\rightarrow\mathbb{R}^{+}$ . Man bezeichnet die Menge der auf definierten Funktionen, die bezüglich der Norm in beschränkt sind, als B(X) und führt auf B(X) mit $\|f\|_{\infty}:=\sup\{\|f(x)\|_V : x\in X\}$ eine Norm ein, die B(X) wiederum zu einem normierten Raum macht. Dann ist eine Familie von auf definierten Funktionen genau dann gleichmäßig beschränkt, wenn sie eine Teilmenge von B(X) ist und als Teilmenge von $(B(X),\|\cdot\|_{\infty})$ beschränkt ist.

Punktweise Beschränktheit

Eine Familie von Funktionen $\mathcal{F}$ auf einer Menge deren Wertevorrat ein normierter Raum ist, heißt punktweise beschränkt, wenn für jeden Punkt $x\in X$ die Menge $\mathcal{F}|_x:=\{f(x)|f \in \mathcal{F}\}$ beschränkt ist. $\mathcal{F}|_x$ ist also die Menge aller Werte, die an der Stelle von irgendeiner Funktion der Familie angenommen werden.

Man beachte:

Eine gleichmäßig beschränkte Familie ist notwendig punktweise beschränkt.
Eine punktweise beschränkte Familie kann unbeschränkte Funktionen enthalten.
Jede gleichmäßig beschränkte Familie besteht aus beschränkten Funktionen, aber nicht jede Familie von beschränkten Funktionen ist gleichmäßig beschränkt.
Eine Familie von beschränkten Funktionen muss nicht punktweise beschränkt sein.

Beispiele

Alle Familien in den Beispielen sind als Funktionenfolgen $(f_n)_{n\in\mathbb{N}}$ definiert. Die Familie ist hier immer $\mathcal{F}=\{ f_n| n\in\mathbb{N}\}$ .

Die Folge der auf $X=\left]0,1\right[$ definierten reellwertigen Funktionen $f_n\colon x\mapsto \tfrac{1}{nx}$ ist punktweise beschränkt. Keine der Funktionen der Familie ist beschränkt, damit ist sie auch nicht gleichmäßig beschränkt.
Die Folge $f_n\colon z\mapsto z^n$ ist auf der Menge $X_0=\{z\in\mathbb{C}| |z|\leq 1\}$ gleichmäßig beschränkt (durch 1). Auf einer beschränkten Teilmenge der komplexen Zahlenebene, die Punkte mit einem Betrag größer 1 enthält, ist die Folge immer noch eine Folge von beschränkten Funktionen aber weder punktweise noch gleichmäßig beschränkt. Auf der Menge $X_2=\mathbb{C}$ ist keine der Funktionen beschränkt und die Folge auch nicht punktweise beschränkt.
Die Folge der konstanten und damit beschränkten reellwertigen Funktionen $f_n \colon x\mapsto n$ auf einer beliebigen nichtleeren Menge ist punktweise unbeschränkt.

Basierend auf einem Artikel in:

Wikipedia.de