Wurzelkriterium
Das Wurzelkriterium ist ein mathematisches Konvergenzkriterium für unendliche Reihen. Es basiert, wie das Quotientenkriterium, auf einem Vergleich mit einer geometrischen Reihe.
Die Grundidee ist folgende: Eine geometrische Reihe mit positiven, reellen
Gliedern konvergiert
genau dann, wenn der Quotient
aufeinanderfolgender Glieder kleiner als 1 ist. Die
-te
Wurzel des
-ten
Summanden dieser geometrischen Reihe strebt gegen
.
Verhält sich eine andere Reihe genauso, ist auch sie konvergent. Da es sich
sogar um absolute
Konvergenz handelt, kann die Regel verallgemeinert werden, indem man die
Beträge betrachtet.
Das Wurzelkriterium wurde zuerst 1821 vom französischen Mathematiker Augustin Louis Cauchy in seinem Lehrbuch „Cours d'analyse“ veröffentlicht. Deswegen wird es auch „Wurzelkriterium von Cauchy“ genannt.
Formulierungen
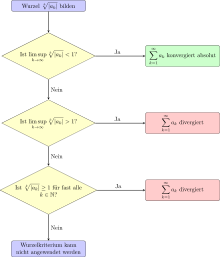
Sei eine unendliche Reihe
mit reellen oder komplexen Summanden
gegeben. Falls man nun
(
steht hier für den Limes superior) oder
für ein
und fast alle Indizes
nachweisen kann, so ist die Reihe
absolut
konvergent. D.h. die Reihe
selbst und auch die Reihe
konvergiert.
Ist jedoch
oder
für unendlich viele Indizes
,
so divergiert die Reihe, da die Reihenglieder keine Nullfolge bilden.
Im Fall
und
für fast alle Indizes
lässt sich nichts über die Konvergenz der Reihe aussagen. So lässt sich
beispielsweise mit dem Wurzelkriterium
keine Aussage über die Konvergenz der allgemeinen
harmonischen Reihe
für
machen, da
.
Für
ist die allgemeine harmonische Reihe divergent, für
konvergent; das Wurzelkriterium kann aber die beiden Fälle nicht unterscheiden.
Beispiele
Beispiel 1. Wir untersuchen die Reihe
auf Konvergenz. Über das Wurzelkriterium erhalten wir:
mit der eulerschen
Zahl .
Somit ist diese Reihe konvergent.
Beispiel 2. Wir prüfen nun die Reihe
auf Konvergenz. Wir erhalten:
Somit ist diese Reihe divergent.
Beweisskizze
Das Wurzelkriterium wurde erstmals von Augustin Louis Cauchy bewiesen. Es folgt mit dem Majorantenkriterium aus Eigenschaften der geometrischen Reihe:
- Denn gilt für alle
, so ist das Majorantenkriterium
mit einer konvergenten geometrischen Reihe
als Majorante erfüllt.
- Daran ändert sich auch nichts, falls dieses Kriterium für die ersten N Glieder der Reihe nicht erfüllt ist.
- Gilt
, so ist
für fast alle n erfüllt, nach Definition des größten Häufungspunktes, womit wieder eine Majorante konstruiert werden kann.
Restgliedabschätzung
Ist die Reihe nach dem Wurzelkriterium konvergent, erhält man noch eine Fehlerabschätzung, d.h. eine Abschätzung des Restglieds der Summe nach N Summanden:
.
Das Wurzelkriterium ist schärfer als das Quotientenkriterium
Sei
eine positive Folge und sei
.
Liefert bei einer Reihe das
Quotientenkriterium
eine Entscheidung (das heißt
im Falle der Konvergenz bzw.
im Falle der Divergenz),
so liefert auch das Wurzelkriterium eine Entscheidung (das heißt
im Falle der Konvergenz bzw.
im Falle der Divergenz).
Dies wird induziert durch die Ungleichungskette
Ist ohne Einschränkung
und
,
so gibt es zu jedem noch so kleinen, aber positiven
(
)
eine Indexschranke
,
ab der gilt:
Multipliziert man die Ungleichung von
bis
durch, so erhält man in der Mitte ein Teleskopprodukt:
Multipliziert man anschließend mit
durch und zieht die
-te
Wurzel, so ist
Für
konvergiert die linke Seite gegen
und die rechte Seite gegen
.
Daher ist
und
Da
beliebig klein gewählt werden kann, folgt daher
und
Sind beispielsweise die Reihenglieder
und
,
dann ist
und
.
Hier ist
und
,
wonach das Quotientenkriterium keine Entscheidung liefert.
Das Wurzelkriterium liefert hier aber eine Entscheidung, weil
ist.
Aus
folgt die Konvergenz von
.
Das Wurzelkriterium ist also echt schärfer als das Quotientenkriterium.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 04.06. 2019