Wurzel (Mathematik)

Grafische Darstellung der Quadratwurzel-Funktion $y={\sqrt {x}}$

In doppeltlogarithmischer Auftragung werden die -ten Wurzeln zu Geraden.

In der Mathematik versteht man unter Wurzelziehen oder Radizieren die Bestimmung der Unbekannten in der Potenz

$a=x^{n}\,$

Hierbei ist eine natürliche Zahl (meist größer als 1) und ein Element aus einem Körper (häufig eine nichtnegative reelle Zahl). Das Ergebnis des Wurzelziehens bezeichnet man als Wurzel oder Radikal (von lat. radix „Wurzel“). Das Radizieren ist eine Umkehrung des Potenzierens.^[1] Im Fall n=2 spricht man von Quadratwurzeln, bei n=3 von Kubikwurzeln. Wurzeln werden mit Hilfe des Wurzelzeichens notiert, im Beispiel ist $x:={\sqrt[{n}]{a}}$ die Wurzel bzw. das Radikal.

Definition, Sprech- und Schreibweisen

Es sei $n\geq 1$ eine natürliche Zahl. Ist eine nichtnegative reelle Zahl, so besitzt die Gleichung

$x^{n}=a$

genau eine nichtnegative reelle Lösung. Diese wird als -te Wurzel aus bezeichnet. Man schreibt dafür:

$x={\sqrt[{n\,}]{a}}$

Hierbei bezeichnet man

${\sqrt[{n\,}]{a}}$ als Wurzel, Radikal oder Radix,
${\sqrt {\;\;}}$ als Wurzelzeichen,
als Wurzelexponent,
als Radikand.^[2]

Im Spezialfall n=1 erhält man ${\sqrt[{1\,}]{a}}=a$ .

Quadrat- und Kubikwurzel

Üblicherweise wird die zweite Wurzel als Quadratwurzel oder einfach nur als die Wurzel bezeichnet und der Wurzelexponent weggelassen:

${\sqrt {a}}={\sqrt[{2}]{a}}$

Die Wurzel mit dem Wurzelexponenten 3 (dritte Wurzel) bezeichnet man auch als Kubikwurzel.

Beispiel:

${\sqrt[{3}]{8}}=2$

(Sprich: Die dritte Wurzel aus 8 ist 2 oder Die Kubikwurzel aus 8 ist 2)

Mathematische Grundlagen

Die folgende Beschreibung des Radizierens als einer rechtseindeutigen Wurzelfunktion bezieht sich auf den angeordneten Körper $\mathbb{R}$ der reellen Zahlen, also gewissermaßen auf die Schulmathematik. Ein allgemeinerer Wurzelbegriff, der den hier beschriebenen umfasst, wird im Artikel Adjunktion (Algebra) behandelt.^[3]

Zusammenhang mit Potenzen

Das Radizieren mit dem Wurzelexponenten und das Potenzieren mit dem Exponenten heben sich gegenseitig auf. Gemäß obenstehender Definition der Wurzel gilt für alle reellen Zahlen $a\geq 0$ und für alle natürlichen Zahlen $n\geq 1$ :

$\left({\sqrt[{n}]{a}}\right)^{n}=a$

Das Radizieren mit dem Wurzelexponenten wirkt wie das Potenzieren mit dem Exponenten ${\tfrac {1}{n}}$ . Nach den Rechenregeln für Potenzen gilt nämlich:

$\left(a^{\frac {1}{n}}\right)^{n}=a^{\frac {n}{n}}=a^{1}=a$

Daher kann das Radizieren mit dem Wurzelexponenten n auch als Potenzieren mit dem Exponenten 1/n interpretiert werden:

${\sqrt[{n}]{a}}=a^{\frac {1}{n}}$

Eindeutigkeit von Wurzeln aus positiven Zahlen

Obwohl die eingangs genannte Fragestellung bei geradzahligen Wurzelexponenten und positiven Radikanden zwei Lösungen mit unterschiedlichen Vorzeichen besitzt, steht die Schreibweise mit dem Wurzelzeichen ${\sqrt[{}]{}}$ grundsätzlich für die positive Lösung.^[4]^[5] Beispielsweise hat die Gleichung $x^{2}=4$ die beiden Lösungen $x=+2$ und x=-2 . Der Term ${\sqrt[{2}]{4}}$ hat jedoch den Wert +2 und nicht den Wert −2. Allgemein gilt daher für geradzahlige Wurzelexponenten

${\sqrt[{2n}]{x^{2n}}}=|x|\,.$

Wurzeln aus negativen Zahlen

Die Behandlung von Wurzeln aus negativen Zahlen ist nicht einheitlich. Es gilt beispielsweise

$(-2)^{3}=-8\,,$

und ist die einzige reelle Zahl, deren dritte Potenz ist. Allgemein ergeben sich für ungerade Potenzen negativer Zahlen wieder negative Zahlen.

Bezüglich der ungeraden Wurzeln aus negativen Zahlen werden folgende Positionen vertreten:

Wurzeln aus negativen Zahlen sind generell nicht definiert. Beispielsweise ist ${\sqrt[{3}]{-8}}$ also undefiniert. Die Lösung der Gleichung $x^{3}=-8$ wird geschrieben als $x=-{\sqrt[{3}]{8}}$ .
Wurzeln aus negativen Zahlen sind definiert, wenn der Wurzelexponent eine ungerade Zahl ist (3, 5, 7, …). Für ungerade Zahlen gilt generell

${\sqrt[{2n+1}]{-a}}=-{\sqrt[{2n+1}]{a}}$ .

Diese Festlegung ist mit manchen Eigenschaften der Wurzeln, die für positive Radikanden gelten, nicht vereinbar. Beispielsweise ist

$-2={\sqrt[{3}]{-8}}\neq {\sqrt[{6}]{(-8)^{2}}}={\sqrt[{6}]{64}}=+2.$

Auch funktioniert diese Festlegung nicht mit der Gleichung ${\sqrt[{k}]{a}}=a^{\frac {1}{k}}=\exp \left({\tfrac {1}{k}}\ln(a)\right)$ , da der (natürliche) Logarithmus von negativen Zahlen nicht definiert ist ( darf also nicht negativ sein).

Wurzeln zu geraden Exponenten aus negativen Zahlen können keine reellen Zahlen sein, weil gerade Potenzen reeller Zahlen nie negativ sind. Es gibt keine reelle Zahl , sodass $x^{2}=-1$ , somit kann man auch keine Wurzel $x={\sqrt[{2}]{-1}}$ finden, die in den reellen Zahlen liegt. Der Bedarf für Wurzeln aus negativen Zahlen führte zur Einführung der komplexen Zahlen; allerdings gibt es beim Wurzelbegriff im Bereich der komplexen Zahlen gewisse Schwierigkeiten mit der eindeutigen Auszeichnung einer der Wurzeln, siehe unten.

Irrationale Wurzeln aus ganzen Zahlen

Ist eine nichtnegative ganze Zahl und eine positive ganze Zahl, so ist ${\sqrt[ {k}]{n}}$ entweder eine ganze oder eine irrationale Zahl. Das beweist man durch Anwendung der Eindeutigkeit der Primfaktorzerlegung:

Ist $n\leqq 1$ , so ist ${\sqrt[{k}]{n}}=n$ , also eine ganze Zahl. Sonst gibt es eine bis auf die Reihenfolge der Faktoren eindeutige Primfaktorzerlegung $n=p_{1}^{e_{1}}\dotsm p_{r}^{e_{r}}$ mit paarweise verschiedenen Primzahlen $p_{1},\dotsc ,p_{r}$ und positiven ganzen Exponenten $e_{1},\dotsc ,e_{r}$ . Sind alle $e_{j}$ für $1\leqq j\leqq r$ durch teilbar, so ist ${\sqrt[{k}]{n}}=p_{1}^{e_{1}/k}\dotsm p_{r}^{e_{r}/k}$ , also eine ganze Zahl.

Zu zeigen ist jetzt noch: Gibt es mindestens ein mit $1\leqq j\leqq r$ , so dass $e_{j}$ nicht durch teilbar ist, so ist ${\sqrt[ {k}]{n}}$ irrational. Der Beweis für die Irrationalität erfolgt indirekt, also durch Widerlegen der gegenteiligen Annahme wie beim Beweis der Irrationalität der Wurzel aus 2 bei Euklid, der im Wesentlichen der Spezialfall n=k=2 dieses Beweises ist.

Angenommen, ${\sqrt[ {k}]{n}}$ wäre rational. Dann könnte man die Zahl als Bruch zweier natürlicher Zahlen und schreiben:

${\sqrt[{k}]{n}}={\frac {a}{b}}$ .

Durch Potenzieren der Gleichung erhält man

$n={\frac {a^{k}}{b^{k}}}$

und daraus folgt

$nb^{k}=a^{k}$ .

Der Primfaktor $p_{j}$ kommt in $a^{k}$ bzw. $b^{k}$ jeweils -mal so oft vor wie in bzw. , jedenfalls in einer durch teilbaren Vielfachheit, wobei natürlich auch das 0-malige Auftreten zugelassen ist. In kommt er voraussetzungsgemäß in der nicht durch teilbaren Vielfachheit $e_{j}$ vor. Also kommt er auf der linken Seite dieser Gleichung nicht in einer durch teilbaren Vielfachheit vor, auf der rechten hingegen schon, und wir erhalten einen Widerspruch zur Eindeutigkeit der Primfaktorzerlegung. Daher ist ${\sqrt[ {k}]{n}}$ irrational.

Die Wurzelgesetze

Die Rechenregeln für Wurzeln ergeben sich aus jenen für Potenzen.

Für positive Zahlen und und $n,m,k\in \mathbb {N}$ gelten die folgenden Rechengesetze:

Produktregel: ${\sqrt[{n}]{a}}\cdot {\sqrt[{n}]{b}}={\sqrt[{n}]{a\cdot b}}$
Quotientenregel: ${\frac {\sqrt[{n}]{a}}{\sqrt[{n}]{b}}}={\sqrt[{n}]{\frac {a}{b}}}$
"Verschachtelungsregel" oder Iterationsregel: ${\sqrt[ {m}]{{\sqrt[ {n}]{a}}}}={\sqrt[ {m\cdot n}]{a}}$
Definition für gebrochenen Exponenten: $a^{\frac {k}{n}}={\sqrt[{n}]{a^{k}}}=\left({\sqrt[{n}]{a}}\right)^{k}$
Definition für negativen Exponenten: $a^{-{\frac {k}{n}}}={\frac {1}{a^{\frac {k}{n}}}}$
Bei gleichem Radikand gilt: ${\sqrt[{m}]{a}}\cdot {\sqrt[{n}]{a}}=a^{{\frac {1}{m}}+{\frac {1}{n}}}={\sqrt[{mn}]{a^{m+n}}}$

Bei negativen Zahlen und dürfen diese Rechengesetze nur angewendet werden, wenn und ungerade Zahlen sind. Bei komplexen Zahlen sind sie gänzlich zu vermeiden, bzw. gilt die Gleichheit nur bei geeigneter Wahl der Nebenwerte. Anders gesagt: werden in einem Beispiel auf der linken Seite irgendwelche Wurzeln (bspw. nur Hauptwerte) ausgewählt, so gibt es für die rechte Seite geeignete Nebenwerte, die die Gleichheit erfüllen – linke und rechte Seite unterscheiden sich um eine Einheitswurzel.

Grenzwerte

Es gelten die folgenden Grenzwerte:

$\lim _{n\rightarrow \infty }{\sqrt[{n}]{a}}=1$ für
$\lim _{n\rightarrow \infty }{\sqrt[{n}]{n}}=1$

Dies folgt aus der Ungleichung $n<\left(1+{\sqrt[{2}]{\tfrac {2}{n}}}\right)^{n}$ , die man mit Hilfe des binomischen Lehrsatzes zeigen kann.

$\lim _{n\to \infty }{\sqrt[{n}]{n^{k}}}=1$ , wobei eine beliebige, aber feste natürliche Zahl ist.
$\lim _{n\rightarrow \infty }{\frac {\ln(n)}{n}}=0$ ,

wie aus der Exponentialdarstellung von ${\sqrt[{n}]{n}}$ hervorgeht.

Wurzelfunktionen

Funktionen der Form

$f\colon \mathbb {R} _{0}^{+}\to \mathbb {R} _{0}^{+},x\mapsto {\sqrt[{n}]{x}}$ oder allgemeiner $x\mapsto {\sqrt[{n}]{x^{m}}}$

heißen Wurzelfunktionen. Sie sind Potenzfunktionen, es gilt ${\sqrt[{n}]{x^{m}}}=x^{\frac {m}{n}}$ .

Berechnung

Wurzeln können durch schriftliches Wurzelziehen bestimmt werden. Dieses Verfahren ähnelt der schriftlichen Division und basiert auf den binomischen Formeln. Es wurde bis in die 1960er Jahre am Gymnasium noch gelehrt, ist heute jedoch von geringer praktischer Bedeutung.

Rückführung auf andere Funktionen

Höhere Wurzeln aus positiven Zahlen kann man wie jede Potenz durch Exponentialfunktion und Logarithmus ausdrücken:

${\sqrt[{n}]{x}}=x^{1/n}=\exp \left({\frac {\ln(x)}{n}}\right)$

Numerische Berechnung

Um einen Näherungswert für eine Wurzel zu erhalten, kann man mehrere Verfahren anwenden. Dazu gehören unter anderem das Intervallhalbierungsverfahren.

Ein weiteres Näherungsverfahren zur Berechnung von ${\sqrt[{n}]{x}}$ ergibt sich, indem man mit dem Newton-Verfahren eine Nullstelle der Funktion

$y\mapsto y^{n}-x,\quad n\geq 1$ annähert:

Wähle einen (möglichst guten) Startwert
Iteriere nach der Vorschrift

$y\mapsto {\frac {(n-1)y^{n}+x}{n\cdot y^{n-1}}}$

Für n=2 erhält man gerade das Heron-Verfahren.

Beispiel für eine Näherung für ${\sqrt[{3}]{2}}$ nach dem obigen Iterationsverfahren:

Die Iterationsvorschrift lautet mit x=2 und n=3

$y\mapsto {\frac {2\,y^{3}+2}{3\,y^{2}}}$ .

Mit dem Startwert y=2 erhält man:

Startwert:	2,000000000000
Schritt 1:	1,500000000000
Schritt 2:	1,296296296296
Schritt 3:	1,260932224741
Schritt 4:	1,259921860565
Schritt 5:	1,259921049895
Schritt 6:	1,259921049894

Methode der „Rechenkünstler“

Man kann, wie es Rechenkünstler machen, eine Wurzel auch durch Abschätzung und Anwendung elementarer Zahlentheorie bestimmen, sofern bekannt ist, dass die Wurzel eine natürliche Zahl ist. Das lässt sich besonders gut am Beispiel der dritten Wurzel zeigen. Dazu muss man zwei Dinge wissen, nämlich die Größenordnung der Kubikzahlen, und die letzte Ziffer der Zahl:

1	1
8	2
27	3
64	4
125	5
216	6
343	7
512	8
729	9
1.000	10

1.000	10
8.000	20
27.000	30
64.000	40
125.000	50
216.000	60
343.000	70
512.000	80
729.000	90
1.000.000	100

Beispiele:

Die dritte Wurzel von 103.823:
Die Zahl liegt zwischen 64.000 und 125.000, deshalb muss die Zehnerstelle der dritten Wurzel 4 sein. Die letzte Ziffer der Zahl ist eine 3, demnach ist die dritte Wurzel von 103.823 abgeschätzt 47.
Die dritte Wurzel von 12.167:
Die Zahl liegt zwischen 8.000 und 27.000, deshalb muss die Zehnerstelle der dritten Wurzel 2 sein. Die letzte Ziffer der Zahl ist eine 7, demnach ist die dritte Wurzel von 12.167 abgeschätzt 23.

Das Ganze funktioniert aber nur dann, wenn man davon ausgehen kann, dass es sich bei der vorgegebenen Zahl um die dritte Potenz einer natürlichen Zahl handelt.

Bei den Aufgaben der Rechenkünstler geht es natürlich um viel höhere Potenzen mehrstelliger Zahlen – zum Beispiel die Berechnung der 25. Wurzel aus 880.794.982.218.444.893.023.439.794.626.120.190.780.624.990.275.329.063.400.179.824.681.489.784.873.773.249 (Lösung: 1729) und extremere Aufgaben.

Wurzeln aus komplexen Zahlen

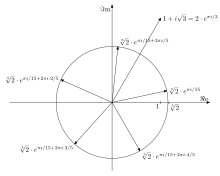
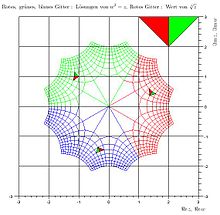
Die fünf fünften Wurzeln aus 1 + i√3 = 2 · e^{π · i/3}

Die drei Lösungen der Gleichung $w^{3}=z$ in der komplexen -Ebene (rotes, grünes, blaues Gitter). Das rote Netz bildet außerdem die Funktion ${\sqrt[{3}]{z}}$ ab. Das große farbige -Dreieck und seine drei -Bilder dienen als Orientierungshilfe.

Die komplexen Zahlen $\mathbb {C}$ werden definiert durch die Adjunktion $\mathbb {C} :=\mathbb {R} (\mathrm {i} )$ der Lösung (Wurzel) $\mathrm {i} :={\sqrt {-1}}$ der Gleichung $\mathrm i^2 = -1$ zu den reellen Zahlen $\mathbb {R}$ . Fasst man die komplexen Zahlen als Ebene $\mathbb{R} \times \mathbb{R}$ auf, in der die reellen Zahlen als eine ausgezeichnete Gerade $\mathbb {R} \times {0}$ die Ebene in zwei Halbebenen teilt und die positiven Zahlen sich rechts befinden, dann wird die Zahl $\mathrm {i}$ in die obere und $-\mathrm i$ in die untere Halbebene platziert. Gleichzeitig mit dieser Orientierung wird der Nullpunkt $(0,0)$ durch die Funktion $\mathrm {e} ^{\mathrm {i} \varphi }$ für wachsendes reelles $\varphi$ im mathematisch positiven Sinn (also entgegen dem Uhrzeigersinn) umlaufen, so dass $\scriptstyle \mathrm {e} ^{\pm {\frac {\pi }{2}}\mathrm {i} }=\pm \mathrm {i}$ ist. Mit dieser Maßgabe lassen sich inhärent mehrdeutige Wurzeln im Komplexen auf eindeutige Real- und Imaginärteile (Hauptwerte) festlegen. Gleichwohl ist bei der Anwendung der Wurzelgesetze die dort erwähnte Sorgfalt zu beachten.

Als die -ten Wurzeln einer komplexen Zahl $a\in \mathbb {C}$ bezeichnet man die Lösungen der Gleichung

$z^{n}=a$ .

Ist $a\neq 0$ in der Exponentialform $a=|a|\,\mathrm {e} ^{\mathrm {i} \varphi }$ dargestellt, so sind die -ten Wurzeln aus genau die komplexen Zahlen

$z_{k}={\sqrt[{n}]{|a|}}\cdot \exp \left({\frac {\mathrm {i} \varphi }{n}}+k\cdot {\frac {2\pi \mathrm {i} }{n}}\right)\quad (k=0,1,\dots ,n-1)$

Der Sonderfall a=1 wird als -te Kreisteilungsgleichung bezeichnet, die Lösungen als -te Einheitswurzeln. Die Bezeichnung „Kreisteilungsgleichung“ erklärt sich, wenn man ihre Lösungen in der Gaußschen Ebene betrachtet: die -ten Einheitswurzeln teilen den Kreis mit dem Radius und dem Koordinatenursprung als Mittelpunkt in gleiche Teile, sie bilden die Eckpunkte eines in den Kreis einbeschriebenen regulären -Ecks.

Anders als bei reellen Zahlen kann man nicht so einfach eine der Wurzeln als die Wurzel auszeichnen; dort wählt man die einzige nichtnegative Wurzel. Man kann jedoch eine (holomorphe) -te Wurzelfunktion für komplexe Zahlen, die keine nichtpositiven reellen Zahlen sind, über den Hauptzweig des komplexen Logarithmus definieren:

$z^{1/n}=\exp {\frac {\ln z}{n}}\quad (z\in \mathbb {C} \setminus \{x\in \mathbb {R} \mid x\leq 0\})$

Die so ausgezeichnete Wurzel bezeichnet man auch als Hauptwert, die anderen als Nebenwerte.

Man kann den Logarithmus auch (unstetig) auf die negative reelle Achse fortsetzen, es gilt dann aber mit der so definierten Wurzelfunktion beispielsweise ${\sqrt[{3}]{-8}}=2\,\exp {{\bigl (}\mathrm {i} \,{\tfrac {\pi }{3}}{\bigr )}}=1+\mathrm {i} {\sqrt {3}}$ und nicht =-2 .^[6]

Literatur

Hans Kreul, Harald Ziebarth: Mathematik leicht gemacht. 7. Auflage. Verlag Harri Deutsch, 2009, ISBN 978-3-8171-1836-6.

Anmerkungen

↑ Die andere Umkehrung ist das Logarithmieren.
↑ Der Wurzelexponent beim Radizieren entspricht dem Logarithmus beim Logarithmieren und dem Exponenten beim Potenzieren. Der Radikand entspricht dem Numerus (Logarithmand) beim Logarithmieren und dem Ergebnis des Potenzierens
↑ Für die Schwierigkeiten mit der Rechtseindeutigkeit s.a. den Wurzeln aus komplexen Zahlen.
↑ DIN 1302:1999 Allgemeine mathematische Zeichen und Begriffe
↑ EN ISO 80000-2:2020 Größen und Einheiten – Teil 2: Mathematik

↑ Dies lässt sich vermeiden mit der Auszeichnung derjenigen Wurzel unter allen, deren Argument $\arg({\sqrt[{n}]{z}})$ modulo $\pi$ den absolut kleinsten Rest liefert. Bei Gleichheit zweier Werte ist dann der in der rechten (positiver Realteil) und der in der oberen Halbebene (positiver Imaginärteil) auszuwählen. Diese Regel ist mit den oben aufgestellten Regeln für reelle Radikanden voll kompatibel. Einige Beispiele:

${\sqrt[{2}]{-1}}=+\mathrm {i} \qquad \qquad {\sqrt[{3}]{-1}}=-1\qquad \qquad {\sqrt[{4}]{-1}}={\frac {{\sqrt {2}}+\mathrm {i} {\sqrt {2}}}{2}}$

Als weiteres Beispiel sei ${\sqrt[{3}]{-\mathrm {i} }}$ angegeben:

Obwohl	$\mathrm {i} ^{3}=-\mathrm {i}$	und	${\biggl (}{\frac {{\sqrt {3}}-\mathrm {i} }{2}}{\biggr )}^{3}=-\mathrm {i}$	und	${\biggl (}{\frac {-{\sqrt {3}}-\mathrm {i} }{2}}{\biggr )}^{3}=-\mathrm {i} ,$
ist	$\mathrm i$	$\neq$	${\sqrt[{3}]{-\mathrm {i} }}={\frac {{\sqrt {3}}-\mathrm {i} }{2}}$	$\neq$	${\frac {-{\sqrt {3}}-\mathrm {i} }{2}}$	mit den absoluten Resten ${\text{mod }}\pi$
des Arguments	$\|\arg(\mathrm {i} )\|={\frac {\pi }{2}}$		${\biggl \|}\arg {\frac {{\sqrt {3}}-\mathrm {i} }{2}}{\biggr \|}={\frac {\pi }{6}}$	$\equiv$	${\frac {\pi }{6}}-\pi =\arg {\frac {-{\sqrt {3}}-\mathrm {i} }{2}}{\text{ mod }}\pi ,$

weil die mittlere Wurzel ${\frac {{\sqrt {3}}-\mathrm {i} }{2}}$ bei dem gleichen absoluten Rest ${\text{mod }}\pi$ einen positiven Realteil hat.

Außerdem bleiben bei dieser Definition die Wurzelgesetze für viele Wurzelexponenten auch bei komplexen Radikanden erhalten, solange für die so ausgewählten Wurzeln die Summen der Reste modulo $\pi$ der Argumentwerte absolut unterhalb ${\tfrac {\pi }{2}}$ bleiben.

Basierend auf einem Artikel in:

Wikipedia.de