Definitionslücke
In dem mathematischen Teilgebiet der Analysis hat eine Funktion Definitionslücken, wenn einzelne Punkte aus ihrem Definitionsbereich ausgeschlossen sind. Üblicherweise geht es dabei um reelle, stetige bzw. differenzierbare Funktionen. Die Definitionslücken sind die Stellen, an denen man durch null teilen müsste oder Ähnliches, beispielsweise bei gebrochenrationalen Funktionen. Die Definitionslücken einer Funktion lassen sich klassifizieren und gegebenenfalls „reparieren“, so dass die Funktion dort mit den gewünschten Eigenschaften fortgesetzt werden kann. In diesem Fall ist die Funktion stetig fortsetzbar und hat stetig hebbare Definitionslücken.
Insbesondere wenn eine Definitionslücke nicht stetig hebbar ist, zum Beispiel weil die Funktion dort gegen unendlich strebt oder sehr schnell oszilliert, wird die Lücke auch als Singularität bezeichnet, wobei der Sprachgebrauch in diesen Fällen nicht immer einheitlich ist. Oft werden Definitionslücke und Singularität als Synonyme verwendet.
Bei komplexwertigen Funktionen, die in einer Umgebung einer Definitionslücke holomorph sind, spricht man von isolierten Singularitäten. Dort ist die Klassifikation einfacher und es gelten weitreichende Aussagen, für die es keine Entsprechungen bei reellen Funktionen gibt.
Definition
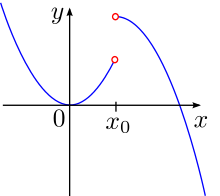
Sei
ein Intervall,
ein Punkt aus dem Inneren des Intervalls und
eine Obermenge
von
.
Eine stetige Funktion
,
die überall auf der Obermenge
außer an der Stelle
definiert ist, hat in
eine Definitionslücke.
Stetig hebbare Definitionslücke
Sei
eine Definitionslücke der stetigen Funktion
.
Existiert eine stetige Funktion
mit
für alle
,
dann ist
eine stetige
Fortsetzung von
.
Die Definitionslücke wird dann stetig hebbar oder stetig behebbar
und die Funktion
stetig ergänzbar oder stetig fortsetzbar genannt.
Existiert der Grenzwert
dann ist
eine stetig hebbare Definitionslücke von
.
In diesem Fall wird durch
eine stetige Fortsetzung
von
ohne Definitionslücke definiert.
Eigenschaften stetiger Fortsetzungen
- Wenn eine stetige Fortsetzung existiert, dann ist sie eindeutig, weil der Grenzwert
-
- eindeutig ist.
- Daraus folgt das Kriterium:
ist genau dann in
stetig fortsetzbar, wenn der Grenzwert
existiert.
- Kann eine Funktion als Bruch dargestellt werden, deren Zähler- und
Nennerfunktion an einer gemeinsamen Nullstelle
differenzierbar sind, so gilt die Regel von de l’Hospital:
- Eine allgemeinere Möglichkeit, um eine stetige Fortsetzung zu finden, bietet der Einschnürungssatz. Er gilt auch für nicht stetige Funktionen.
- Eine Fortsetzung ist zwar immer stetig, aber gegebenenfalls nicht
differenzierbar. Die Betragsfunktion
ist auf
differenzierbar aber kann auf null nicht differenzierbar fortgesetzt werden. Selbst wenn eine Fortsetzung glatt ist, muss sie nicht analytisch sein.
- Im Komplexen gelten aufgrund der Eigenschaften holomorpher Funktionen weitergehende Aussagen: Eine stetige Fortsetzung ist schon eine analytische Fortsetzung. Der Riemannsche Hebbarkeitssatz sagt aus, dass die Definitionslücke einer holomorphen Funktion schon hebbar ist, wenn die Funktion in einer passenden Umgebung der Definitionslücke beschränkt ist. Im Reellen gilt keine vergleichbare Aussage; es könnte dort auch eine nicht hebbare Sprungstelle vorliegen.
Weitere Arten von Definitionslücken
Neben den stetig hebbaren Definitionslücken gibt es noch verschiedene Arten von Sprungstellen sowie Polstellen und wesentliche Singularitäten. Funktionen mit solchen Definitionslücken können nicht stetig fortgesetzt werden.
Beispiele
- Die Funktion
ist in ihrem gesamten Definitionsbereich
stetig, hat aber an der Stelle 0 eine Definitionslücke. Dies ist eine Polstelle.
- Gegeben sei
- Die Funktion
ist in
stetig fortsetzbar, denn für den Grenzwert gilt
- und somit lautet die Fortsetzung
.
- An diesem Beispiel kann man noch bemerken, dass
auch ohne Fallunterscheidung geschrieben werden kann, es gilt nämlich
für alle
.
- In anderen Fällen kann es sein, dass die Fallunterscheidung unumgänglich ist. So hat etwa
-
- die stetige Fortsetzung
.
Gebrochenrationale Funktionen
Eine gebrochenrationale Funktion ist der Quotient
aus zwei ganzrationalen
Funktionen
und
.
Eine gebrochenrationale Funktion hat genau dann eine Definitionslücke, wenn die rationale Funktion im Nenner eine Nullstelle hat. Funktionen dieser speziellen Klasse können als Definitionslücken nur Polstellen oder stetig hebbare Definitionslücken aufweisen.
Die Definitionslücke kann nur dann stetig hebbar sein, wenn die
ganzrationalen Funktionen im Nenner und Zähler an derselben Stelle eine
Nullstelle haben. Für die ganzrationalen Funktionen
und
ist das Verhalten an den Nullstellen bekannt:
Die Nullstellen der Zähler- und Nennerfunktionen lassen sich
ausfaktorisieren. Wenn also
und
an der Stelle
eine Nullstelle haben, so ist immer
und
wobei
.
Die natürlichen
Zahlen
und
bezeichnet man auch als die Ordnung (oder Vielfachheit) der jeweiligen
Nullstelle.
Offensichtlich kann man die gemeinsamen Faktoren der Nullstellen (zumindest
für )
kürzen. Das Ergebnis der Kürzung ist der einzige Kandidat für eine stetige
Fortsetzung nach
.
- Wenn
, dann liegt eine stetig behebbare Definitionslücke vor, wobei der Grenzwert durch 0 gegeben ist.
- Wenn
, dann liegt eine stetig behebbare Definitionslücke vor, wobei der Grenzwert durch
gegeben ist.
- Wenn
, dann liegt eine Polstelle vor.
Beispiel
Die Funktion
hat für
eine Lücke, die sich durch Kürzen mit dem Wert
beheben lässt, wodurch sich die Funktion
als auch bei
stetige Fortsetzung ergibt. Es ist wohlgemerkt
ebenso wie
für
undefiniert, dort liegt eine Polstelle vor.
Ein Beispiel, um die Unterscheidung zwischen einer Polstelle und einer behebbaren Definitionslücke zu veranschaulichen. Die Funktion
hat für
eine Definitionslücke, die durch Kürzen mit dem Wert
auf die Funktion
führt.
Da
ebenso wie
für
undefiniert ist, wurde die Lücke durch das Kürzen nicht behoben. Daher liegt
bei
eine Polstelle und keine behebbare Definitionslücke vor.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.04. 2021