Ganzrationale Funktion
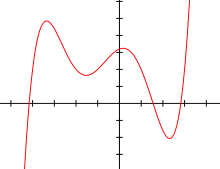
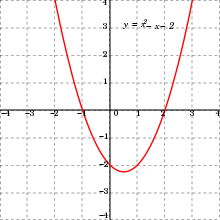
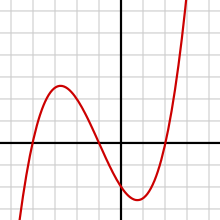
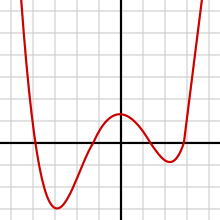
Eine ganzrationale Funktion oder Polynomfunktion ist in der Mathematik eine Funktion, die als Summe von Potenzfunktionen mit natürlichen Exponenten beschrieben werden kann. Somit können solche Funktionen ausschließlich mittels der Operationen Addition, Subtraktion und Multiplikation beschrieben werden. Ganzrationale Funktionen gehören zu den rationalen Funktionen und enthalten ihrerseits als Spezialfälle die linearen und quadratischen Funktionen.
Dieser Artikel beschäftigt sich hauptsächlich mit den in der Schulmathematik üblichen ganzrationalen Funktionen über den reellen Zahlen. Weiterführende Informationen zu möglichen Verallgemeinerungen des Konzepts finden sich im Artikel Polynom.
Definition
Eine ganzrationale Funktion ist eine reelle Funktion, die sich in der Gestalt
schreiben lässt, wobei
eine natürliche
Zahl und
reelle
Zahlen sind und
gilt.
Die Zahl
heißt Grad der Funktion, die Zahlen
sind ihre Koeffizienten.
Der Koeffizient
wird als Leitkoeffizient bezeichnet. Der Summand
heißt Absolutglied, die Summanden
und
werden manchmal als lineares beziehungsweise quadratisches Glied bezeichnet.
Außerdem ist auch die reelle Funktion
eine ganzrationale Funktion; sie wird auch das Nullpolynom genannt. Auf diese
Weise sind alle endlichen Summen von Summanden der Gestalt
mit beliebigen reellen Zahlen
ganzrationale Funktionen. Da bei der konstanten Nullfunktion keines der
ungleich Null ist, ist für diese ganzrationale Funktion kein Grad definiert.
Die hier angegebene Darstellung der ganzrationalen Funktion ist ihre Normalform. Beispielsweise kann man eine ganzrationale Funktion auch mittels Linearfaktoren oder mittels des Horner-Schemas darstellen.
Beispiele
- Die Funktion mit dem Term
ist eine ganzrationale Funktion vom Grad 3 mit den Koeffizienten
und
.
- Bei der Funktion
muss der Funktionsterm zunächst durch Auflösen der Klammern in eine Summe umgeschrieben werden:
-
- der Grad ist also 4 und die Koeffizienten sind
und
.
- Bei einer ganzrationalen Funktion vom Grad
mit den Koeffizienten
kann der Funktionsterm geschrieben werden als
.
Spezialfälle
- Ohne einen definierten Grad gibt es das Nullpolynom
, eine konstante Funktion
- Für
und
ergeben sich weitere konstante Funktionen
- Für
ergeben sich lineare Funktionen
(statt
schreibt man für die Steigung hier also
, und statt
für den
>-Achsenabschnitt also
).
- Für
ergeben sich quadratische Funktionen
(statt
und
schreibt man hier also
,
und
).
- Für
ergeben sich kubische Funktionen
.
- Für
spricht man manchmal von quartischen Funktionen.
- Ist nur
und alle anderen Koeffizienten sind gleich
, so ergibt sich eine Potenzfunktion
mit natürlichem Exponenten.
Algebraische Eigenschaften
Die Addition und die Multiplikation zweier ganzrationaler Funktionen ergeben
wieder ganzrationale Funktionen. Somit bildet die Menge der ganzrationalen
Funktionen eine Algebra
über .
Für den Grad ganzrationaler Funktionen
und
gelten die Abschätzung beziehungsweise Gleichheit
und
.
Dabei bezeichnet
den Grad von
.
Außerdem ist auch die Verkettung zweier ganzrationaler Funktionen wieder eine ganzrationale Funktion, das heißt, man erhält wieder eine ganzrationale Funktion, wenn man für die Funktionsvariable eine ganzrationale Funktion einsetzt.
Symmetrie
- Sind alle Exponenten
gerade
Zahlen, so ist der Graph der Funktion achsensymmetrisch
zur y-Achse. Die Funktion heißt dann auch gerade; es gilt
.
- Sind alle Exponenten
ungerade
Zahlen, so ist der Graph der Funktion punktsymmetrisch
zum Ursprung. Die Funktion heißt dann auch ungerade; es gilt
.
- Treten sowohl gerade als auch ungerade Exponenten auf, so hat der Graph keine einfache Symmetrie; er kann aber dennoch symmetrisch zu anderen Achsen oder Punkten sein.
Beispiele:
- Der Graph der Funktion
ist symmetrisch zur
-Achse (nur gerade Exponenten: 6, 4 und 2).
- Der Graph der Funktion
ist symmetrisch zum Ursprung (nur ungerade Exponenten: 7 und 1).
- Der Graph der Funktion
hat keine einfache Symmetrie (ungerade und gerade Exponenten: 3 und 0), ist aber punktsymmetrisch zu seinem Wendepunkt
.
- Der Graph jeder ganzrationalen Funktion zweiten Grades ist achsensymmetrisch zur senkrechten Achse durch seinen Scheitelpunkt.
- Der Graph jeder ganzrationalen Funktion dritten Grades ist punktsymmetrisch zu seinem Wendepunkt.
Grenzverhalten
Allgemein wird das Verhalten für
durch den Summanden mit dem höchsten Exponenten, das Verhalten für
durch die Summanden mit den niedrigsten Exponenten bestimmt.
Wachstum
Ganzrationale Funktionen können als Linearkombinationen von Potenzen aufgefasst werden. Daher wachsen sie (für hinreichend große Werte) langsamer als jede exponentielle Funktion, deren Basis größer als 1 ist, unabhängig von den Koeffizienten.
Verhalten für sehr große und sehr kleine x-Werte
Alle ganzrationalen Funktionen divergieren
für .
Das genaue Verhalten hängt davon ab, ob der Grad n gerade oder ungerade
ist, und welches Vorzeichen
der Leitkoeffizient
hat; der Graph verhält sich dabei genauso wie der Graph einer Potenzfunktion mit dem
Term
.
Angegeben ist im Folgenden außerdem die daraus folgende Wertemenge
für den Fall, dass die Definitionsmenge
ist.
| n gerade | n ungerade | |
|---|---|---|
| Der Graph verläuft von links oben nach
rechts oben, also: |
Der Graph verläuft von links unten nach
rechts oben, also: | |
| Der Graph verläuft von links unten nach
rechts unten, also: |
Der Graph verläuft von links oben nach
rechts unten, also: |
Verhalten für x-Werte nahe null
Alle ganzrationalen Funktionen sind für
endlich. Genauer gilt: der Graph schneidet die
-Achse
bei
,
die Steigung an dieser Stelle ist durch
gegeben. Die Tangente im Schnittpunkt mit
der
-Achse
hat also immer die Gleichung
Beispiel
Der Graph der Funktion
verläuft für
wie der Graph der Funktion
,
also von links oben nach rechts unten (Grad
ungerade, Leitkoeffizient
).
Für die Funktionswerte gilt also:
für
und
für
.
Für
verläuft er dagegen wie der Graph von
,
er schneidet die
-Achse
also bei
und hat dort die Steigung
.
Nullstellen
Als Nullstellen einer
ganzrationalen Funktion
werden jene Werte
bezeichnet, für die der Funktionswert null ist, das heißt, die die Gleichung
erfüllen. Eine ganzrationale Funktion hat stets höchstens so viele Nullstellen,
wie ihr Grad angibt. Die konstante Funktion
,
das Nullpolynom, hat unendlich viele Nullstellen. Die ganzrationalen Funktionen
vom Grad 0, nämlich die konstanten Funktionen
für ein
,
haben dagegen keine Nullstellen, so wie es ihrem Grad entspricht.
Linearfaktorzerlegung
Ist der Funktionsterm einer ganzrationalen Funktion als Produkt von linearen Faktoren (von denen manche auch mehrfach auftreten können) und evtl. einer ganzrationalen Funktion g ohne Nullstellen gegeben, also
so sind
die Nullstellen. Die natürlichen
Zahlen
heißen die Vielfachheiten der Nullstellen.
Beispiel: Die Funktion
hat die dreifache Nullstelle ,
die einfache Nullstelle
und die doppelte/zweifache Nullstelle
;
die Faktoren
und
können dagegen für kein
zu null werden, liefern also keine weiteren Nullstellen.
Die Linearfaktorzerlegung einer ganzrationalen Funktion kann man beispielsweise mit Hilfe der Polynomdivision bestimmen. Aus dem Fundamentalsatz der Algebra folgt, dass sich so jede ganzrationale Funktion über den komplexen Zahlen in ein Produkt aus Linearfaktoren zerlegen lässt. Hat die Funktion nur reelle Koeffizienten, so folgt, dass mit jeder komplexen Nullstelle auch die jeweils konjugiert komplexe Zahl eine Nullstelle ist. Damit ergibt sich: jede ganzrationale Funktion über den reellen Zahlen kann (bis auf die Reihenfolge) eindeutig als ein Produkt aus linearen und quadratischen Termen dargestellt werden.
Die Vielfachheit von Nullstellen hängt auch direkt mit den Ableitungen der
Funktion zusammen:
ist genau dann eine
-fache
Nullstelle von
,
wenn gilt
und
.
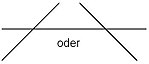
Verlauf des Graphen bei den Nullstellen
- Bei jeder Nullstelle von ungerader Vielfachheit
schneidet der Graph die
-Achse. Die Funktionswerte wechseln dort also ihr Vorzeichen. Bei einfachen Nullstellen wird die
-Achse in einem Winkel größer als 0° geschnitten. Bei jeder Nullstelle ungerader Vielfachheit größer gleich drei ist die Steigung an der Nullstelle 0; der Funktionsgraph hat einen Terrassenpunkt.
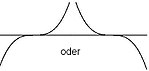
- Bei jeder Nullstelle von gerader
Vielfachheit berührt der Graph die
-Achse. Die Funktionswerte wechseln dort also ihr Vorzeichen nicht. Bei jeder solchen Nullstelle hat der Funktionsgraph einen Extrempunkt.
graphische Veranschaulichung:
| einfache Nullstelle | drei-, fünf-, 2k+1-fache Nullstelle | doppelte, vier-, 2k-fache Nullstelle |
|---|---|---|
 |
 |
 |
Berücksichtigt man außerdem noch das Verhalten für ,
so ergibt sich für das obige Beispiel
folgender Graph:
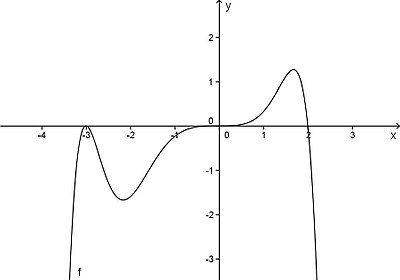
Anzahl von Nullstellen
Mit Hilfe der Polynomdivision
kann man zeigen, dass eine ganzrationale Funktion vom Grad
höchstens
Nullstellen haben kann (Vielfachheiten mitgezählt).
Betrachtet man zusätzlich auch noch das Verhalten des Graphen für ,
das Verhalten an den Nullstellen (Vorzeichenwechsel)
und die Stetigkeit,
so folgt außerdem: ist der Grad gerade bzw. ungerade, so ist die gesamte Anzahl
der Nullstellen (Vielfachheiten mitgezählt) gerade bzw. ungerade. Insbesondere
folgt: Jede ganzrationale Funktion von ungeradem Grad hat mindestens eine
Nullstelle.
Außerdem gibt es noch andere, weiterführende Regeln für die Anzahl der Nullstellen wie beispielsweise die Vorzeichenregel von Descartes und die sturmsche Kette.
Der Fundamentalsatz
der Algebra besagt, dass ein ganzrationale Funktion vom Grad
mindestens eine komplexe
Nullstelle hat (reiner Existenzsatz). Dann hat es genau
Nullstellen, wenn die Nullstellen entsprechend ihrer Vielfachheit gezählt
werden. So ist beispielsweise die Nullstelle
der Funktion
eine doppelte. Im Ergebnis lässt sich jede ganzrationale Funktion
positiven Grades in ein Produkt
von Linearfaktoren
zerlegen.
Nullstellenschranken
Die Lage aller Nullstellen einer ganzrationalen Funktion vom Grad
lässt sich durch Nullstellenschranken, in deren Berechnung nur die
Koeffizienten und der Grad des Polynoms eingehen, abschätzen.
Reelle Nullstellenschranken
Ein wichtiger Spezialfall sind reelle Nullstellenschranken. Eine Zahl
heißt reelle Nullstellenschranke einer ganzrationalen Funktion
,
wenn alle reellen Nullstellen von
im Intervall
liegen; sie heißt obere reelle Nullstellenschranke von
,
wenn alle reellen Nullstellen von
kleiner oder gleich
sind. Analog sind untere Nullstellenschranken erklärt.
Es folgen Beispiele reeller Nullstellenschranken für ganzrationale Funktionen
,
deren führender Koeffizient eins ist. Jede ganzrationale Funktion kann durch
eine Division auf diese Form gebracht werden. Für einige reelle
Nullstellenschranken spielt die Teilindexmenge
der echt negativen Koeffizienten von
eine besondere Rolle,
bezeichnet deren Anzahl.
ist eine obere reelle Nullstellenschranke (Cauchy-Regel),
ist eine obere reelle Nullstellenschranke (Newton-Regel),
ist eine obere reelle Nullstellenschranke (Regel von Lagrange und Maclaurin), dabei bezeichnet
den Betrag des betragsgrößten negativen Koeffizienten und
den Exponenten des höchsten Gliedes mit negativem Koeffizienten;
- Jedes
, das die Ungleichung
-
- erfüllt, ist eine reelle Nullstellenschranke (solche
> sind sogar Schranken für die Beträge komplexer Nullstellen komplexer Polynome). Spezialfälle hiervon sind (siehe auch Satz von Gerschgorin)
-
und
.
Komplexe Nullstellenschranken
Betrachtet man Polynomfunktionen
mit komplexen Koeffizienten, deren Definitionsbereich
ist, dann sind Kreise um den Nullpunkt der komplexen
Zahlenebene das Pendant zu den reellen Nullstellenschranken, deren Radius so
groß zu wählen ist, dass alle (bzw. je nach Anwendung auch nur „einige“)
komplexen Nullstellen der Polynomfunktion auf der Kreisscheibe mit diesem Radius
liegen. Eine Zahl
heißt komplexe Nullstellenschranke der Polynomfunktion
,
wenn alle Nullstellen von
auf der Kreisscheibe um den Nullpunkt mit Radius
liegen (oder anders formuliert: wenn der Betrag jeder Nullstelle kleiner oder
gleich
ist). Ein Ergebnis für komplexe Polynomfunktionen ist:
- Jedes
, das die Ungleichung
- erfüllt, definiert einen Kreis in der komplexen Ebene mit Radius
um den Nullpunkt, der genau
komplexe Nullstellen enthält. Diese Ungleichung ist für
immer lösbar, aber nicht notwendig für jeden Index
.
- Im Fall
ergibt sich die schon für reelle Polynome angegebene Schranke für den Betrag aller Nullstellen. Alle dort angegebenen direkten Berechnungen von
gelten weiter.
- Im Fall
ergibt sich ein Kreis, der keine Nullstellen enthält.
ist dann eine Schranke für alle Nullstellen des „reziproken“ Polynoms
.
Lösungsformeln
Prinzipiell gibt es mehrere Möglichkeiten, die Nullstellen einer ganzrationalen Funktion zu bestimmen. Allgemeine Iterationsverfahren, wie das Newton-Verfahren und die Regula falsi oder auf Polynomfunktionen spezialisierte Iterationsverfahren, wie das Bairstow-Verfahren oder das Weierstraß-(Durand-Kerner)-Verfahren sind einerseits auf jede Polynomfunktion anwendbar, verlieren allerdings bei mehrfachen oder dicht beieinanderliegenden Nullstellen an Genauigkeit und Konvergenzgeschwindigkeit.
Lineare Gleichungen können direkt durch Äquivalenzumformungen gelöst werden. Die Nullstellen sind dann immer einfach. Für quadratische Gleichungen, kubische Gleichungen und quartische Gleichungen gibt es allgemeine Lösungsformeln.
Für Polynome höheren Grades gibt es Lösungsformeln, sofern diese spezielle Formen haben:
- Reziproke Polynomfunktionen haben die Form
-
- das heißt, für den
-ten Koeffizienten gilt
; anders gesagt: die Koeffizienten sind symmetrisch. Für diese Funktionen und solche, die eine leichte Modifikation dieser Symmetriebedingung erfüllen, kann die Nullstellenbestimmung mit Hilfe der Substitution
(bzw.
) auf eine Polynomgleichung reduziert werden, deren Grad halb so groß ist.
- Binome haben die Form
- Setzt man den Koeffizienten
als reell voraus, so sind die
Lösungen Vielfache der komplexen
-ten Einheitswurzeln:
,
- wobei
durchläuft.
- Kann man eine Nullstelle durch ein beliebiges Verfahren oder durch Ausprobieren herausfinden, so kann man den zugehörigen Linearfaktor mit Hilfe einer Polynomdivision herausdividieren und erhält eine algebraische Gleichung niedrigeren Grades. Die Vielfachheiten der Nullstellen ergeben sich hier einfach, indem man abzählt, wie häufig eine Nullstelle jeweils in der Rechnung herauskommt. Für das Finden einer Nullstelle durch Probieren sind dabei folgende Sätze hilfreich:
- Polynomfunktionen, die nur gerade Potenzen von
enthalten, haben die Form:
- Die Lösung erfolgt durch die Substitution
. Hat man eine Lösung für
gefunden, so ist zu berücksichtigen, dass daraus zwei Lösungen für
abzuleiten sind:
und
- Polynomfunktionen, die nur ungerade Potenzen von
enthalten, haben die Form:
-
- Hier ist offensichtlich 0 eine Nullstelle des Polynoms. Man dividiert das
Polynom durch
aus und behandelt es dann wie ein Polynomfunktion
-ten Grades, das nur gerade Potenzen von
enthält.
Differenzier- und Integrierbarkeit
Ableitungsfunktion
Ganzrationale Funktionen sind über ganz
stetig
differenzierbar. Funktionen, die über ganz
beziehungsweise über ganz
differenzierbar sind, heißen ganze
Funktionen. Die Ableitungsfunktion
kann mit Hilfe der Faktor-,
Summen- und Potenzregel bestimmt
werden. Damit erhält man für die Funktion mit der Vorschrift
die Ableitungsfunktion
.
Integrierbarkeit und Stammfunktion
Auf einem kompaktem Intervall ist jede ganzrationale Funktion integrierbar. Außerdem hat jede ganzrationale Funktion eine Stammfunktion. Diese kann mit den üblichen Integral-Regeln explizit angeben werden. Es gilt:
wobei
eine beliebige Konstante ist.
Beispiele
Für die Funktion mit dem Term
ergibt sich die Ableitungsfunktion mit dem Term
Für die Stammfunktionen erhält man in diesem Fall
Extremstellen
Zur Bestimmung der Extremstellen müssen zunächst die Stellen mit waagrechter
Tangente, also die Nullstellen der ersten Ableitung, berechnet werden. Die erste
Ableitung ist wieder eine ganzrationale Funktion, allerdings vom Grad ;
es können also dieselben Methoden wie bei der Nullstellenberechnung benutzt
werden.
Allgemeine Regeln
- Hat die Funktion selbst eine Nullstelle gerader Vielfachheit, so hat ihr Graph dort einen Extrempunkt (siehe oben bei Nullstellen).
- Wechselt die erste Ableitung an einer Stelle ihr Vorzeichen von - nach +, so ist dort eine Minimalstelle; wechselt es von + nach -, so ist dort eine Maximalstelle; wechselt das Vorzeichen nicht, so ist dort keine Extremstelle (aber ein Terrassenpunkt).
- Ist die zweite Ableitung bei einer Nullstelle der ersten Ableitung positiv bzw. negativ, so wechselt die erste Ableitung dort ihr Vorzeichen von - nach + (Minimalstelle) bzw. von + nach - (Maximalstelle). Ist die zweite Ableitung gleich null, so kann an dieser Stelle dennoch eine Extremstelle sein, es kann dort aber auch ein Terrassenpunkt sein. Zur Unterscheidung sind dann andere Mittel als die zweite Ableitung nötig.
- Hat eine Nullstelle der ersten Ableitung ungerade Vielfachheit, so hat die Funktion selbst dort eine Extremstelle; hat sie dagegen gerade Vielfachheit, so hat die Funktion an dieser Stelle einen Terrassenpunkt.
Anzahl
Aus dem Satz über die Anzahl der Nullstellen einer ganzrationalen Funktion
folgt, dass eine ganzrationale Funktion vom Grad
höchstens
Extremstellen haben kann.
Betrachtet man zusätzlich auch noch das Verhalten des Graphen für
und das Verhalten an den Nullstellen (Vorzeichenwechsel), so folgt außerdem: ist
der Grad gerade bzw. ungerade, so ist die gesamte Anzahl der Extremstellen
ungerade bzw. gerade.
Insbesondere folgt: Jede ganzrationale Funktion von geradem Grad hat ein
absolutes Minimum oder Maximum (je nachdem, ob der Leitkoeffizient
positiv oder negativ ist).
Wendestellen
Zur Bestimmung der Wendestellen müssen zunächst die Nullstellen der zweiten
Ableitung, die sogenannten Flachstellen, berechnet werden. Die zweite Ableitung
ist wieder eine ganzrationale Funktion, allerdings vom Grad ;
es können also dieselben Methoden wie bei der Nullstellenberechnung benutzt
werden.
Allgemeine Regeln
- Hat die Funktion selbst eine Nullstelle ungerader Vielfachheit größer gleich drei, so hat ihr Graph dort einen Terrassenpunkt, also auch einen Wendepunkt (siehe oben bei Nullstellen).
- Wechselt die zweite Ableitung an einer Stelle ihr Vorzeichen, so ist dort eine Wendestelle.
- Ist die dritte Ableitung bei einer Nullstelle der zweiten Ableitung ungleich Null, so wechselt die zweite Ableitung dort ihr Vorzeichen (Wendestelle). Ist die dritte Ableitung gleich null, so kann an dieser Stelle trotzdem eine Wendestelle sein, muss aber nicht. Zur Unterscheidung sind dann andere Mittel als die dritte Ableitung nötig.
- Hat eine Nullstelle der zweiten Ableitung gerade Vielfachheit, so hat die Funktion selbst dort keine Wendestelle; hat die Nullstelle der ersten Ableitung dagegen ungerade Vielfachheit, so hat die Funktion selbst dort eine Wendestelle. Ist zusätzlich auch die erste Ableitung an dieser Stelle gleich null, so hat der Graph der Funktion dort einen Terrassenpunkt.
- Insbesondere bei Funktionen dritten Grades gilt:
- Hoch- und Tiefpunkt (wenn vorhanden) liegen immer symmetrisch zum Wendepunkt (dies folgt, da die Graphen von Funktionen dritten Grades immer symmetrisch zu ihrem Wendepunkt sind, siehe oben).
- Hat die Funktion selbst drei (nicht notwendigerweise verschiedene) reelle Nullstellen, so ergibt sich die Wendestelle als ihr Mittelwert, gewichtet mit den Vielfachheiten. (Gibt es dagegen nur eine reelle Nullstelle, so müssen bei der Mittelwertbildung auch die komplexen Nullstellen mit berücksichtigt werden.)
Anzahl
Aus dem Satz über die Anzahl der Nullstellen einer ganzrationalen Funktion
folgt, dass eine ganzrationale Funktion vom Grad
höchstens
Wendestellen haben kann.
Betrachtet man zusätzlich auch noch das Verhalten des Graphen für
und das Verhalten an den Nullstellen (Vorzeichenwechsel), so folgt außerdem: ist
der Grad gerade bzw. ungerade, so ist die gesamte Anzahl der Wendestellen gerade
bzw. ungerade.
Insbesondere folgt: Jede ganzrationale Funktion von ungeradem Grad größer gleich drei hat mindestens eine Wendestelle.
Aufstellen von Funktionstermen
Oft ist ein Problem folgender Art zu lösen: Gegeben sind einige Punkte und
evtl. zusätzliche Bedingungen (wie beispielsweise Steigungen in diesen Punkten),
und es ist eine ganzrationale Funktion gesucht, deren Graph durch diese Punkte
verläuft und ggf. die zusätzlichen Bedingungen erfüllt. Um diese ganzrationale
Funktion zu finden, stellt man zunächst den Funktionsterm in der allgemeinst
möglichen Form auf (der Grad ist entweder direkt gegeben oder muss aus den
anderen gegebenen Angaben ermittelt werden), bildet evtl. notwendige Ableitungen
der Funktion in dieser allgemeinen Form und setzt dann die gegebenen Bedingungen
ein. Dies führt auf ein lineares
Gleichungssystem für die Koeffizienten der Funktion; diese bezeichnet man
statt ,
usw. hier meist mit
usw. Durch Lösen dieses Gleichungssystems erhält man dann den Term der gesuchten
Funktion.
Beispiel: Gesucht ist eine ganzrationale Funktion möglichst niedrigen Grades,
deren Graph symmetrisch zur -Achse
ist und im Wendepunkt
die Steigung 2 hat.
- Da der Graph symmetrisch zur
-Achse sein soll, muss der Grad gerade sein, und der Funktionsterm kann nur gerade Exponenten enthalten.
- Da es einen Wendepunkt geben soll, kann der Grad nicht 2 sein (eine Funktion zweiten Grades hat keinen Wendepunkt); der niedrigst mögliche Grad ist also 4.
- Der Funktionsterm in allgemeinster Form ist also:
- Da hier von einem Wendepunkt die Rede ist, benötigt man zwei Ableitungen:
- Der Graph verläuft durch den Punkt
, also gilt (
- und
-Koordinate in
einsetzen)
- Der Graph hat dort die Steigung 2, also gilt (>
-Koordinate und Steigung in
einsetzen)
- Der Punkt
ist ein Wendepunkt, also gilt (
muss bei Wendestelle gleich 0 sein)
- Insgesamt ergibt sich also das lineare Gleichungssystem
- Lösen dieses Gleichungssystems ergibt
. Der Term der gesuchten Funktion ist also:
Anwendungsbeispiele
- Viele in Natur und Technik vorkommende Kurven kann man durch ganzrationale Funktionen relativ gut beschreiben, beispielsweise Geländeformationen, Sprungschanzen oder die Durchbiegung von Balken.
- In geometrischen Anwendungen tauchen häufig ganzrationale Funktionen auf.
Beispiele:
- Schneidet man an den Ecken einer rechteckigen Pappe (Länge
, Breite
) jeweils Quadrate der Seitenlänge
aus und faltet die Pappe dann zu einer oben offenen Schachtel, so ist das Volumen der Schachtel
.
- Stapelt man Kugeln (z.B. Orangen im Supermarkt) zu einer
dreiseitigen Pyramide auf, wobei entlang einer Grundkante
Kugeln liegen, so enthält die Pyramide insgesamt
Kugeln.
- Schneidet man an den Ecken einer rechteckigen Pappe (Länge
- Steuertarife werden häufig durch ganzrationale Funktionen beschrieben.
- In wirtschaftlichen Anwendungen ist die Erlösfunktion häufig eine ganzrationale Funktion dritten Grades.
- Da ganzrationale Funktionen besonders einfach sind, werden oft kompliziertere Funktionen durch ganzrationale angenähert (vgl. Taylorreihe und Approximationssatz von Weierstraß). Dieses Vorgehen wird insbesondere in der Analysis und der Numerik eingesetzt. Alternativ gibt es auch Situationen, in denen eine endliche Anzahl von Funktionswerten vorgegeben sind und eine Funktion gesucht wird, die durch diese Punkte verläuft. Dazu kann die Polynominterpolation eingesetzt werden. Außerdem kann man eine endliche Menge von Funktionswerten auch stückweise durch ganzrationale Funktionen interpolieren. Dieses Vorgehen heißt Splineinterpolation. Möchte man eine ganzrationale Funktion an einem Punkt numerisch effizient (für Computer optimiert) auswerten, so kann das Horner-Schema eingesetzt werden.
Literatur
- H. Schneider, G. Stein: Mathematik 11 und Mathematik 12: Analysis für nichttechnische Ausbildungsrichtungen der Fachoberschule.
- R. Schöwe, J. Knapp, R. Borgmann: Analysis: Kaufmännisch-wirtschaftliche Richtung für Fachoberschule.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 21.01. 2021