
Kubische Gleichung
Kubische Gleichungen sind Polynomgleichungen dritten Grades, also algebraische Gleichungen der Form
wobei die
als Koeffizienten bezeichnet
werden, Elemente eines Ringes
sind und
ist. Bei den wichtigsten Anwendungen ist
der Körper der reellen
oder komplexen Zahlen. Im
letzteren Fall hat die kubische Gleichung nach dem Fundamentalsatz
der Algebra stets drei komplexe Lösungen
,
die auch zusammenfallen können. Mit ihrer Hilfe lässt sich das Polynom in faktorisierter
Form darstellen:
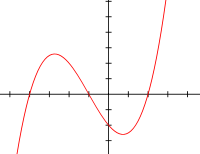
Im Falle reeller Koeffizienten stellt die Menge der Paare
geometrisch eine kubische Parabel in der
-
-Ebene
dar, also den Graph einer kubischen
Funktion. Dessen Nullstellen,
also seine Schnittpunkte mit der
-Achse,
sind die reellen Lösungen der kubischen Gleichung. Der Funktionsgraph hat nach
dem Zwischenwertsatz
stets mindestens eine reelle Nullstelle, jedoch höchstens drei.
Lösungsansätze
Raten einer Lösung
Verfahren
Kennt man eine Lösung
exakt, so kann man das kubische Polynom mit Hilfe der Polynomdivision oder
des Horner-Schemas durch
dividieren und erhält so eine quadratische
Gleichung. Diese kann man mit Hilfe einer Lösungsformel lösen und
erhält so die restlichen Lösungen der kubischen Gleichung. Dieses Verfahren ist
aber nur für eine rationale
Lösung
praktikabel. Bereits bei der irreduziblen
Gleichung
ist das Verfahren mit der noch relativ einfachen Lösung
nicht mehr praktikabel, da die Koeffizienten der verbleibenden quadratischen
Gleichung sehr kompliziert werden. In diesen Fällen lassen sich die Lösungen mit
der unten genannten Cardanischen
Formel leichter bestimmen.
Sind alle Koeffizienten der kubischen Gleichung ganzzahlig,
so kann man versuchen, eine rationale Lösung zu raten, das heißt, durch
Probieren zu finden. Ist der führende Koeffizient
vom Betrag gleich 1, so kann man die ganzzahligen Teiler des letzten
Koeffizienten
durchprobieren (auch negative Werte!). Ist
von eins verschieden, so müssen alle Brüche, deren Zähler ein Teiler von
und deren Nenner ein Teiler von
ist, durchprobiert werden. Der Satz
über rationale Nullstellen garantiert, dass man mit diesem endlichen Aufwand
eine rationale Nullstelle findet, falls eine solche existiert. Sind die
Koeffizienten rational, so kann man ganzzahlige Koeffizienten erreichen, indem
man die Gleichung mit dem Hauptnenner
aller Koeffizienten multipliziert.
Beispiel
Als rationale Lösungen der kubischen Gleichung
kommen nur die ganzzahligen Teiler
des letzten Koeffizienten sowie
in Frage. In der Tat ist
eine Lösung, wovon man sich durch Einsetzen überzeugt. Polynomdivision liefert
und mit der quadratischen Lösungsformel ergeben sich als weitere Lösungen
.
Algebraische Bestimmung
Im Folgenden wird angenommen, dass der Koeffizientenring
wenigstens ein Integritätsbereich
ist, zu dem ein Quotientenkörper
gebildet werden kann. In den besonders wichtigen Fällen ist
der angeordnete
Körper
der reellen Zahlen mit der Ordnungsrelation
.
Charakteristik 2 und 3
Hat der Koeffizientenring
die Charakteristik
oder
dann lassen sich die nachfolgenden Formeln, insbesondere die Cardanische, wegen
der Divisionen durch
nicht anwenden – im Fall
lässt sich die Gleichung nicht einmal auf die reduzierte
Form bringen.
Ein wichtiges Hilfsmittel zur Untersuchung der Nullstellen ist die formale Ableitung
,
die, wenn sie nicht konstant ist, eine einzige Wurzel hat, denn sie ist im Fall
linear und im Fall
vom Grad 2 mit einer zweifachen Nullstelle. Durch Bilden des größten
gemeinsamen Teilers
kann festgestellt werden, ob
mehrfache Nullstellen hat.
Reduktion der Gleichung auf eine Normalform
Es gibt eine Reihe äquivalenter Umformungen der kubischen Gleichung durch Lineartransformation
des Arguments, die es erlauben, diese für das nachfolgende Lösungsverfahren zu
vereinfachen (Tschirnhaus-Transformation).
Durch Division durch
kann das Polynom zunächst normiert
werden.
Durch Lineartransformation des Arguments mit Hilfe der Substitution
ergibt sich folgender Term:
Ist die Charakteristik
des Koeffizientenrings
von 3 verschieden, dann lässt sich das quadratische Glied durch die Wahl von
beseitigen und man erhält die reduzierte Form der kubischen Gleichung:
Die reduzierte Form mit
kann nun mit Hilfe der Cardanischen
Formeln aufgelöst und durch anschließende Rücksubstitution können die
Lösungen der ursprünglichen Gleichung bestimmt werden. Hierdurch ist die
Gesamtheit der reellen und komplexen Lösungen zugänglich.
Analytische Bestimmung der reellen Lösungen der reellen Gleichung
Im Fall, dass das ursprüngliche Polynom nur reelle Koeffizienten hat, kann
mithilfe der Diskriminante
überprüft werden, ob ausschließlich reelle Lösungen vorliegen:
Ist ,
so sind alle Lösungen reell. Andernfalls gibt es genau eine reelle Lösung, die
andern beiden sind komplex nicht-reell und konjugiert zueinander.
Der Fall p = 0
Fall 1:
- Hier wählt man
und erhält
. Nach Rücksubstitution ergibt sich eine einzige reelle Lösung zu
.
Unterfall 1a:
und
- Die einzige reelle Lösung
und
hat die Vielfachheit 3.
Die Fälle mit p ≠ 0
Eine Lösungsstrategie für die verbleibenden Lösungen, die ohne die Verwendung
komplexer Zahlen auskommt, ist die folgende:
Die reduzierte Form wird durch
Substitution mit Hilfe einer geeigneten trigonometrischen
oder hyperbolischen
Funktion so umgeformt, dass sie auf bekannte Additionstheoreme
zurückgeführt werden kann.
Geeignete Funktionen sind:
| Funktion |
Wertebereich | Additionstheorem | kubische Gleichung | Fall | |
| 2 | |||||
| 3 | |||||
| 3 | |||||
| beliebig reell | 4 |
Die aufgeführten Additionstheoreme sind so parametrisiert, dass sie sich in dieselbe kubische Gleichung überführen lassen, die sich mit der reduzierten Form der gegebenen Gleichung
zur Deckung bringen lässt. Mithilfe der Setzung
erhält man durch Koeffizientenvergleich
sofort
und
.
Somit lässt sich
durch die ursprünglichen Koeffizienten
und
ausdrücken:
,
wobei
gesetzt ist und
eine zugehörige Arkus-
oder Areafunktion bezeichnet.
Durch Rücksubstitution kann dann die endgültige Lösung der kubischen Gleichung
ermittelt werden. Aus
,
und
erhält man somit
.
Als erstes bestimmt das Vorzeichen von
die Wahl der Substitutionsfunktion
,
in zweiter Linie
,
das im reellen Wertebereich von
liegen muss.
Fall 2:
(woraus
und
folgt):
- Substitution mit
, entspricht
- Es ergeben sich drei mögliche Lösungen zu
mit
und
Unterfall 2a:
(woraus
folgt):
- Es gibt nur zwei Lösungen. Die reduzierte Form vereinfacht sich zu
. Aus den Linearfaktoren lassen sich nun direkt die zwei Lösungen
und
ablesen. Zum selben Ergebnis führt
, also
bzw.
. Entsprechend ist
und
. Die letztere Lösung hat die Vielfachheit 2.
Fall 3:
und
(woraus
und
folgt):
- Substitution mit
, entspricht
, also
- Zunächst hat man zwei Lösungen
, die wegen
wieder in eins geworfen werden. Also:
mit
.
Grenzfall 3a:
und
(woraus
folgt):
, also
und
.
Bemerkung:
Die zwei anderen (rein-imaginären) Lösungenvon
werden durch die Anwendung von
ins Reelle zurückgeworfen:
. Das Ergebnis ist wie im Unterfall 2a:
und
.
Fall 4:
und
:
- Substitution mit
, entspricht
- Als Ergebnis folgt:
mit
- Es ergibt sich eine reelle Lösung.
Schnelle numerische Berechnung
Die Methode von Deiters und Macías-Salinas
bringt die kubische Funktion zunächst einmal in die Form
und verwendet dann die Laguerre-Samuelson-Ungleichung,
um Schranken für die Lösungen zu finden.
.
Hierbei ist ,
und
ist der Abszissenwert des Wendepunkts. Dann sind folgende Fälle zu
unterscheiden:
: Dann ist die Wendestelle die erste Lösung,
.
: Dann ist
eine Lösung.
- Andernfalls wird iterativ eine Näherungslösung
bestimmt. Dies geschieht ausgehend vom Startwert
-
-
- mit dem Halley-Verfahren:
.
-
Anschließend wird durch Polynomdivision
die quadratische
Funktion
(mit kleinem
,
dessen Betrag von der erzielten Genauigkeit abhängt) gebildet, deren Nullstellen
(im Fall
)
direkt ausgerechnet werden können:
mit
und
.
Bei sorgfältiger Implementierung (siehe revidierte Zusatzinformationen zur Originalpublikation) ist dieses Verfahren auf modernen Prozessoren (2014, Architektur x86-64) um den Faktor 1,2 bis 10 schneller als die auf vergleichbare Genauigkeit ausgewerteten Cardanischen Formeln.
Siehe auch
Literatur
- Peter Gabriel: Matrizen, Geometrie, Lineare Algebra. Birkhäuser, Basel 1996, ISBN 3-7643-5376-7.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 10.12. 2025