Primzahlsatz
Der Primzahlsatz erlaubt eine Abschätzung der Verteilung der Primzahlen mittels Logarithmen. Der Zusammenhang zwischen Primzahlen und Logarithmen wurde bereits von dem 15-jährigen Carl Friedrich Gauß 1793 und unabhängig von ihm durch Adrien-Marie Legendre 1798 vermutet, aber erst 1896 unabhängig von Jacques Salomon Hadamard und Charles-Jean de La Vallée Poussin bewiesen.
Die Primzahlfunktion
Im Weiteren sei
die Primzahlfunktion, die für beliebige reelle Zahlen
definiert ist als die Anzahl der Primzahlen, die nicht größer als
sind. Formal kann man schreiben:
Dabei bezeichnet das Symbol
die Menge der Primzahlen, die Schreibweise
steht für die Anzahl
der Elemente der Menge
Der Primzahlsatz
Der Primzahlsatz besagt:
Nennt man zwei reelle Funktionen
und
asymptotisch
äquivalent, wenn der Quotient
für
gegen 1 konvergiert, so kann man den Primzahlsatz auch so formulieren: Die
Funktionen
und
sind asymptotisch äquivalent.
Der Primzahlsatz ist im Wesentlichen äquivalent dazu, dass die riemannsche
Zetafunktion keine Nullstellen
mit
hat.
Es gibt verschiedene analytische Beweise. Ein einfacher Beweis, der die Abschätzung der Zetafunktion im Unendlichen nach Hadamard und La Vallée Poussin vermeidet, wurde von Donald Newman gegeben. Ein dritter Weg innerhalb der analytischen Zahlentheorie benutzt die Taubersätze von Wiener-Ikehara, vermeidet ebenfalls die Abschätzung im Unendlichen, benutzt aber tieferliegende Ergebnisse aus der Theorie der Fourier-Transformation. Es gibt auch Beweise ohne Verwendung komplexer Funktionentheorie („elementare“ Beweise nach Paul Erdős und Atle Selberg).
Stärkere Formen des Primzahlsatzes
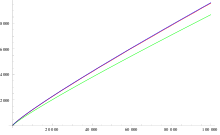
Bessere Approximationen
als
liefert der Integrallogarithmus
Die Integraldarstellung für
wird gewählt, weil die Stammfunktionen
von
nicht elementar
sind.
Der Integrallogarithmus ist asymptotisch äquivalent zu
also auch zu
Man kann zeigen:
mit einer positiven Konstanten .
Dabei ist
ein Landau-Symbol,
d.h., es gibt eine Konstante
,
sodass
für alle
gilt. Die Verbesserung des Fehlerterms hängt davon ab zu zeigen, dass die
Zetafunktion in immer größeren Bereichen im kritischen Streifen nullstellenfrei
ist. Unter Annahme der Riemannschen
Vermutung (nach der alle nicht-trivialen Nullstellen auf der Geraden
liegen), und nur unter dieser, kann man die Fehlerabschätzung zu
verbessern (Helge von Koch 1901). Eine nicht-asymptotische Schranke fand Lowell Schoenfeld unter Annahme der Riemann-Vermutung:
.
Geschichte
Adrien-Marie Legendre veröffentlichte 1798 als erster in seiner Théorie des
nombres (Abhandlung über Zahlentheorie) unabhängig von Gauß
den vermuteten Zusammenhang zwischen Primzahlen und Logarithmen. In der zweiten
Auflage dieses Werks 1808 verbesserte er die Abschätzung von
zu ungefähr gleich
(wo dieser Wert 1,08366 verantwortlich für das Problem der Existenz der Legendre-Konstanten ist). Ein erster Schritt hin zu einem Beweis gelang Pafnuti Lwowitsch Tschebyschow, der 1851 die folgende schwächere Form des Primzahlsatzes zeigte:
für alle hinreichend großen .
Das heißt, dass die Anzahl der Primzahlen unter einer gegebenen Größe um nicht
mehr als ungefähr 10 % nach oben oder unten von der logarithmischen
Funktion
abweicht.
Der englische Mathematiker James Joseph Sylvester, damals Professor an der amerikanischen Johns Hopkins University in Baltimore,
verfeinerte 1892 Tschebyschows Methode und zeigte, dass für die Ungleichung bei
hinreichend großem
die untere Grenze 0,95695 und die obere Grenze 1,04423 genügt, die
Abweichung also maximal nur mehr ungefähr 5 % beträgt.
In seiner berühmten Arbeit Über die Anzahl der Primzahlen unter einer gegebenen Größe (1859) hat Bernhard Riemann den Zusammenhang zwischen der Verteilung der Primzahlen und den Eigenschaften der Riemannschen Zetafunktion gezeigt. Der deutsche Mathematiker Hans von Mangoldt bewies 1895 das Hauptresultat der Riemannschen Arbeit, dass der Primzahlsatz dem Satz äquivalent ist, dass die Riemannsche Zetafunktion keine Nullstellen mit Realteil 1 hat. Sowohl Hadamard als auch de la Vallée Poussin haben 1896 die Nichtexistenz solcher Nullstellen bewiesen. Ihre Beweise des Primzahlsatzes sind also nicht „elementar“, sondern verwenden funktionentheoretische Methoden. Lange Jahre galt ein elementarer Beweis des Primzahlsatzes für unmöglich, was 1949 durch die von >Atle Selberg und Paul Erdős gefundenen Beweise widerlegt wurde (wobei „elementar“ hier keineswegs „einfach“ bedeutet). Später wurden noch zahlreiche Varianten und Vereinfachungen dieser Beweise gefunden.
Zahlenbeispiele
Die folgende Tabelle zeigt konkrete Werte der Primzahlfunktion im Vergleich mit den Logarithmen, Legendres Formel und dem Integrallogarithmus.
| 10 | 4 | 0,400000 | 4 | 0 | 0,921034 | 8 | 6 | 2 |
| 102 | 25 | 0,250000 | 22 | 3 | 1,151293 | 28 | 30 | 5 |
| 103 | 168 | 0,168000 | 145 | 23 | 1,160503 | 172 | 178 | 10 |
| 104 | 1.229 | 0,122900 | 1.086 | 143 | 1,131951 | 1.231 | 1.246 | 17 |
| 105 | 9.592 | 0,095920 | 8.686 | 906 | 1,104320 | 9.588 | 9.630 | 38 |
| 106 | 78.498 | 0,078498 | 72.382 | 6.116 | 1,084490 | 78.543 | 78.628 | 130 |
| 107 | 664.579 | 0,066458 | 620.421 | 44.158 | 1,071175 | 665.140 | 664.918 | 339 |
| 108 | 5.761.455 | 0,057615 | 5.428.681 | 332.774 | 1,061299 | 5.768.004 | 5.762.209 | 754 |
| 109 | 50.847.534 | 0,050848 | 48.254.942 | 2.592.592 | 1,053727 | 50.917.519 | 50.849.235 | 1.701 |
| 1010 | 455.052.511 | 0,045505 | 434.294.482 | 20.758.029 | 1,047797 | 455.743.004 | 455.055.615 | 3.104 |
| 1011 | 4.118.054.813 | 0,041181 | 3.948.131.654 | 169.923.159 | 1,043039 | 4.124.599.869 | 4.118.066.401 | 11.588 |
| 1012 | 37.607.912.018 | 0,037608 | 36.191.206.825 | 1.416.705.193 | 1,039145 | 37.668.527.415 | 37.607.950.281 | 38.263 |
| 1013 | 346.065.536.839 | 0,034607 | 334.072.678.387 | 11.992.858.452 | 1,035899 | 346.621.096.885 | 346.065.645.810 | 108.971 |
| 1014 | 3.204.941.750.802 | 0,032049 | 3.102.103.442.166 | 102.838.308.636 | 1,033151 | 3.210.012.022.164 | 3.204.942.065.692 | 314.890 |
| 1015 | 29.844.570.422.669 | 0,029845 | 28.952.965.460.217 | 891.604.962.452 | 1,030795 | 29.890.794.226.982 | 29.844.571.475.288 | 1.052.619 |
| 1016 | 279.238.341.033.925 | 0,027924 | 271.434.051.189.532 | 7.804.289.844.393 | 1,028752 | 279.660.033.612.131 | 279.238.344.248.557 | 3.214.632 |
| 1017 | 2.623.557.157.654.233 | 0,026236 | 2.554.673.422.960.305 | 68.883.734.693.281 | 1,026964 | 2.627.410.589.445.923 | 2.623.557.165.610.822 | 7.956.589 |
| 1018 | 24.739.954.287.740.860 | 0,024740 | 24.127.471.216.847.324 | 612.483.070.893.536 | 1,025385 | 24.775.244.142.175.635 | 24.739.954.309.690.415 | 21.949.555 |
| 1019 | 234.057.667.276.344.607 | 0,023406 | 228.576.043.106.974.646 | 5.481.624.169.369.960 | 1,023982 | 234.381.646.366.460.804 | 234.057.667.376.222.382 | 99.877.775 |
| 1020 | 2.220.819.602.560.918.840 | 0,022208 | 2.171.472.409.516.259.138 | 49.347.193.044.659.701 | 1,022725 | 2.223.801.523.570.829.204 | 2.220.819.602.783.663.484 | 222.744.644 |
| 1021 | 21.127.269.486.018.731.928 | 0,021127 | 20.680.689.614.440.563.221 | 446.579.871.578.168.707 | 1,021594 | 21.154.786.057.670.023.133 | 21.127.269.486.616.126.182 | 597.394.254 |
| 1022 | 201.467.286.689.315.906.290 | 0,020147 | 197.406.582.683.296.285.296 | 4.060.704.006.019.620.994 | 1,020570 | 201.721.849.105.666.574.218 | 201.467.286.691.248.261.498 | 1.932.355.208 |
| 1023 | 1.925.320.391.606.803.968.923 | 0,019253 | 1.888.236.877.840.225.337.614 | 37.083.513.766.578.631.309 | 1,019639 | 1.927.681.221.597.738.628.080 | 1.925.320.391.614.054.155.139 | 7.250.186.216 |
| 1024 | 18.435.599.767.349.200.867.866 | 0,018436 | 18.095.603.412.635.492.818.797 | 339.996.354.713.708.049.069 | 1,018789 | 18.457.546.327.619.878.007.916 | 18.435.599.767.366.347.775.144 | 17.146.907.278 |
| 1025 | 176.846.309.399.143.769.411.680 | 0,017685 | 173.717.792.761.300.731.060.452 | 3.128.516.637.843.038.351.228 | 1,018009 | 177.050.792.039.110.236.839.710 | 176.846.309.399.198.930.392.619 | 55.160.980.939 |
| 1026 | 1.699.246.750.872.437.141.327.603 | 0,016992 | 1.670.363.391.935.583.952.504.342 | 28.883.358.936.853.188.823.261 | 1,017292 | 1.701.156.120.834.278.630.173.694 | 1.699.246.750.872.593.033.005.724 | 155.891.678.121 |
| 1027 | 16.352.460.426.841.680.446.427.399 | 0,016352 | 16.084.980.811.231.549.172.264.034 | 267.479.615.610.131.274.163.365 | 1,016629 | 16.370.326.243.373.272.895.062.280 | 16.352.460.426.842.189.113.085.405 | 508.666.658.006 |
| OEIS | Folge A006880 in OEIS | Folge A057834 in OEIS | Folge A057835 in OEIS | Folge A058289 in OEIS | Folge A057754 in OEIS | Folge A057752 in OEIS |
Die Größe
heißt Primzahldichte.
Vergleicht man
mit den Werten von
in der Tabelle, scheint es so, als ob stets
gelten würde. Tatsächlich wechselt die Differenz
bei größer werdendem
das Vorzeichen
unendlich oft, wie J. E. Littlewood
1914 zeigen konnte.
Die gaußsche Formel unterschätzt also die Anzahl der Primzahlen in einem
hinreichend großen Zahlenbereich, den Stanley Skewes 1933
mit der nach ihm benannten Skewes-Zahl
nach oben abschätzen konnte.
Russell Sherman Lehman stellte 1966 einen wichtigen Satz über die obere Grenze
auf und konnte sie auf eine „handhabbare“ Größe von 1,165·101165
drücken.
Unter Verwendung des Lehmanschen Satzes gelang es dem niederländischen
Mathematiker Herman te Riele 1986 zu zeigen, dass es zwischen
6,627·10370 und 6,687·10370 mehr als 10180
aufeinanderfolgende Zahlen
gibt, für die
gilt.
Den derzeit besten untersten Wert, ebenfalls ausgehend von den Ergebnissen
Lehmans, ermittelten im Jahr 2000 die beiden Mathematiker Carter Bays und
Richard Hudson, die zeigten, dass ein solcher von Littlewood bewiesener Wechsel
vor 1,398244·10316 auftritt.
Obwohl sie dies nicht beweisen konnten, legen ihre Berechnungen nahe, dass sie
tatsächlich den ersten Vorzeichenwechsel gefunden haben. Genauer vermuten sie,
dass die Ungleichung
für
immer gilt.
Explizite Formeln zur Primzahlfunktion
Formeln für Primzahlfunktionen gibt es in zwei Arten: arithmetische Formeln und analytische Formeln. Analytische Formeln für die Primzahlenzählung waren die ersten, die verwendet wurden, um den Primzahlsatz zu beweisen. Sie stammen aus der Arbeit von Bernhard Riemann und Hans von Mangoldt und sind allgemein als explizite Formeln bekannt.
Wir haben folgenden Ausdruck für :
wobei
und
der zweiten Tschebyschow-Funktion.
Hier sind
die Nullstellen der Riemannschen
Zetafunktion im kritischen Streifen, bei dem der Realteil von
zwischen Null und Eins liegt. Die Formel gilt für Werte von
größer als eins, d. h. die Region von Interesse. Die Summe über den Wurzeln ist
bedingt konvergent und sollte in der Reihenfolge zunehmender Absolutwerte des
Imaginärteils genommen werden. Zu beachten ist, dass die gleiche Summe über die
trivialen Wurzeln den letzten Subtrahenden in der Formel ergibt.
Ähnlich wie für
kann auch für die von Riemann eingeführte Primzahlen abzählende Funktion
eine Mittelung an den Sprungstellen
eingeführt werden. Für
haben wir die kompliziertere Formel
Auch hier gilt die Formel wieder für ,
während
die nicht-trivialen Nullstellen der Riemannschen
Zetafunktion nach ihrem Absolutwert geordnet sind, und letzteres Integral
wiederum mit Minuszeichen genommen ist genau die gleiche Summe, aber über den
trivialen Nullstellen. Der erste Ausdruck
ist die übliche logarithmische Integralfunktion; der Ausdruck
im zweiten Term sollte als
betrachtet werden, wobei
die analytische Fortsetzung der exponentiellen Integralfunktion von der
positiven Realen zur komplexen Ebene mit entlang der negativen Realen Achse
geschnittenem Ast ist.
Somit ergibt sich wenn man wie oben eine an den Sprungstellen mittelnde
Funktion
einführt mit der Möbius-Inversionsformel
gültig für ,
wobei
die sogenannte Riemannsche R-Funktion ist.
Die letztgenannte Reihe dafür ist bekannt als Gram-Reihe
und konvergiert für alle positiven .
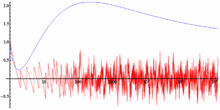
Die Summe über nichttriviale Nullstellen der Zetafunktion in der Formel für
beschreibt die Schwankungen von
,
während die restlichen Terme den „glatten“ Teil der Primzahlfunktion
ausmachen.
Somit kann man
als den besten Fit der
für
bezeichnen.
Die Amplitude des „verrauschten“ Teils liegt heuristisch bei ca. ,
womit die Schwankungen der Primzahlenverteilung mit der
-Funktion
dargestellt werden können:
Eine umfangreiche Tabelle mit den Werten von
steht zur Verfügung.
Primzahlsatz für arithmetische Progressionen, Satz von Siegel-Walfisz
Sei
die Anzahl der Primzahlen kleiner gleich
in der arithmetischen
Progression
,
wobei
koprim sind (
).
Peter Gustav Lejeune Dirichlet und
Adrien-Marie Legendre vermuteten, dass asymptotisch
mit
der Eulerschen
Phi-Funktion (der Anzahl zu
teilerfremden Zahlen kleiner als
).
Das wurde von Charles-Jean de La Vallée Poussin bewiesen mit ähnlichen Methoden wie beim Beweis des
Primzahlsatzes.
Als Beispiel kann man das auf die Verteilung der Primzahlen auf ihre
Endziffern im Dezimalsystem anwenden (analog gilt das für jede Basis). Es kommen
nur die Ziffern 1, 3, 7, 9 in Betracht (außer für die Primzahlen 5 und 2 selbst)
und aus dem Primzahlsatz für arithmetische Progressionen folgt, dass die
Primzahlen unter ihren Endziffern gleich verteilt sind. Es gibt allerdings
einige Ungleichgewichte, die Gegenstand der Forschung sind. So gibt es numerisch
meist mehr Primzahlen der Form
als
unterhalb einer bestimmten Grenze, obwohl die Primzahlen asymptotisch auf beide
Klassen gleich verteilt sind (Chebyshev's Bias,
auch Primzahl-Rennen, nach Pafnuti Lwowitsch Tschebyschow).
Nach John Edensor Littlewood wechselt
auch unendlich oft das Vorzeichen. Ähnliche Phänomene gibt es bei Betrachtung
anderer Kongruenzen als solchen mod
.
Wie K. Soundararajan und Oliver 2016 fanden, gibt es auch Abweichungen der
Gleichverteilung wenn man die Verteilung der Endziffern bei aufeinanderfolgenden
Primzahlen betrachtet.
Genauer wurde die Verteilung in arithmetischen Progressionen durch Arnold Walfisz
untersucht im Satz von Siegel und Walfisz (er basiert auf einem Resultat von Carl Ludwig Siegel).
Der Satz liefert einen asymptotischen Fehlerterm
für die obige Formel. Dabei ist
eine Konstante und
eine beliebige Zahl mit
.
Ursprünglich ist der Satz von Siegel und Walfisz für die Funktion
formuliert mit der Mangoldt-Funktion
.
Mit den bereits eingeführten Bezeichnungen (sowie wie oben
,
)
besagt der Satz dann, dass es für jedes N eine Konstante
gibt so dass:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 20.04. 2021