
Laurent-Reihe
Die Laurent-Reihe (nach Pierre Alphonse Laurent) ist eine unendliche Reihe
ähnlich einer Potenzreihe,
aber zusätzlich mit negativen Exponenten.
Allgemein hat eine Laurent-Reihe in
mit Entwicklungspunkt
diese Gestalt:
Dabei sind die
und
meist komplexe
Zahlen, es gibt aber auch andere Möglichkeiten, die im Abschnitt Formale
Laurent-Reihen weiter unten beschrieben sind. Für komplexe Laurent-Reihen
benutzt man meist die Variable
anstatt
.
Summanden, in denen
ist, werden meist nicht mitgeschrieben, deshalb muss nicht jede Laurent-Reihe in
beide Richtungen ins Unendliche reichen. Genauso wie es bei Potenzreihen
gehandhabt wird und ähnlich wie bei der Darstellung abbrechender Dezimalbrüche, bei denen
formal unendlich viele Nullen hinter der letzten Ziffer stehen.
Die Reihe der Terme mit negativen Exponenten nennt man den Hauptteil der Laurent-Reihe, die Reihe der Terme mit nichtnegativen Exponenten nennt man den Nebenteil.
Eine Laurent-Reihe mit verschwindendem Hauptteil ist eine Potenzreihe, hat sie außerdem nur endlich viele Terme dann ist sie ein Polynom. Hat eine Laurent-Reihe insgesamt nur endlich viele Terme (mit negativem oder positivem Exponent), dann nennt man sie ein Laurent-Polynom.
Die Laurent-Reihe wurde 1843 von dem französischen Mathematiker Pierre Alphonse Laurent vorgestellt. Aufzeichnungen im Nachlass des deutschen Mathematikers Karl Weierstrass deuten jedoch darauf hin, dass dieser sie bereits 1841 entdeckt hatte.
Laurent-Zerlegung
Das Prinzip der Entwicklung einer holomorphen
Funktion in eine Laurent-Reihe basiert auf der Laurent-Zerlegung. Dazu
betrachte man ein Kreisringgebiet .
Nun definiere man zwei holomorphe Funktionen
und
:
.
Das heißt, die Funktionen
und
sind auf einer Kreisscheibe von Radius
bzw.
um den Mittelpunkt holomorph. Da das Argument der Funktion
innerhalb des so definierten Kreisgebietes liegen muss erkennt man schnell, dass
die Funktion
für Werte
definiert ist. Damit ist auch die Summe der beiden Funktionen
auf dem Kreisring
analytisch. Es lässt sich zeigen, dass sich jede auf einem Ringgebiet holomorphe
Funktion auf diese Weise zerlegen lässt. Setzt man dazu noch
voraus, so ist die Zerlegung eindeutig.
Entwickelt man diese Funktion nun in Form von Potenzreihen so ergibt sich folgende Darstellung:
.
Dabei wurde
definiert. Außerdem folgt
aus der Bedingung
.
Erweitert man diese Überlegungen nun auf die Entwicklung um einen Punkt
,
und nicht so wie eben um den Ursprung, so ergibt sich die eingangs angeführte
Definition der Laurent-Reihe für eine holomorphe Funktion
um den Entwicklungspunkt
:
Beispiel
Im Folgenden bezeichnet
wahlweise die reellen
oder komplexen Zahlen.
.
Die Funktion ist unendlich oft reell differenzierbar,
sie ist jedoch an der Stelle
nicht komplex
differenzierbar und hat dort sogar eine wesentliche
Singularität.
Indem man nun
in die Potenzreihenentwicklung der Exponentialfunktion
einsetzt, erhält man die Laurent-Reihe von
mit Entwicklungspunkt
:
Sie konvergiert für jede komplexe Zahl .
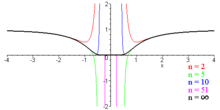
Das Bild rechts zeigt, wie sich die Partialsummenfolge
an die Funktion annähert.
Konvergenz von Laurent-Reihen
Laurent-Reihen sind wichtige Hilfsmittel der Funktionentheorie, vor allem zur Untersuchung von Funktionen mit isolierten Singularitäten.
Laurent-Reihen beschreiben komplexe Funktionen, die auf einem Kreisring holomorph sind, so wie Potenzreihen Funktionen beschreiben, die auf einer Kreisscheibe holomorph sind.
Sei
eine Laurent-Reihe in
mit komplexen Koeffizienten
und Entwicklungspunkt
.
Dann gibt es zwei eindeutig bestimmte Zahlen
und
,
so dass Folgendes gilt:
- Die Laurent-Reihe konvergiert auf dem offenen Kreisring
normal, also insbesondere absolut und lokal gleichmäßig. Damit meint man, dass Haupt- und Nebenteil normal konvergieren. Lokal gleichmäßige Konvergenz impliziert gleichmäßige Konvergenz auf jeder kompakten Teilmenge von
, also insbesondere auf den Bildern von Kurven in
. Die Laurent-Reihe definiert auf
eine holomorphe Funktion
.
- Außerhalb des Kreisrings divergiert die Laurent-Reihe. Das heißt, dass für
jeden Punkt im Äußeren von
,
, die Reihe der Terme mit positiven oder die Terme mit negativen Exponenten divergiert.
- Auf dem Rand des Kreisrings kann man keine allgemeinen Aussagen machen,
außer dass es mindestens einen Punkt auf der äußeren Begrenzung und mindestens
einen Punkt auf der inneren Begrenzung gibt, in die
nicht holomorph fortgesetzt werden kann.
Es ist möglich, dass
und
ist, es kann aber auch sein, dass
ist. Die beiden Radien können wie folgt mit der Formel
von Cauchy-Hadamard berechnet werden:
Man setzt
und
in der zweiten Formel.
Umgekehrt kann man mit einem Kreisring
und einer auf
holomorphen Funktion
beginnen. Dann existiert immer eine eindeutig bestimmte Laurent-Reihe mit
Entwicklungspunkt
,
die (mindestens) auf
konvergiert und dort mit
übereinstimmt. Für die Koeffizienten gilt
für alle
und ein
.
Wegen des Integralsatzes
von Cauchy kommt es auf die Auswahl von
nicht an.
Der Fall ,
also der einer holomorphen Funktion
auf einer gelochten Kreisscheibe um
,
ist besonders wichtig. Der Koeffizient
der Laurentreihenentwicklung von
heißt Residuum
von
in der isolierten Singularität
,
er spielt eine große Rolle im Residuensatz.
Formale Laurent-Reihen
Formale Laurent-Reihen sind Laurent-Reihen in der Unbestimmten ,
die ohne Rücksicht auf Konvergenzbetrachtungen benutzt werden. Die Koeffizienten
können dann aus einem beliebigen kommutativen
Ring stammen. In dieser
Situation ist es jedoch nur sinnvoll, Laurent-Reihen mit nur endlich vielen
negativen Exponenten zu betrachten, also mit einem so genannten endlichen
Hauptteil, und die Entwicklungsstelle mit
wegzulassen.
Zwei solche formale Laurent-Reihen sind per Definition genau dann gleich,
wenn sie in allen Koeffizienten übereinstimmen. Zwei Laurent-Reihen werden
addiert, indem ihre entsprechenden Koeffizienten addiert werden und weil sie nur
endlich viele Terme mit negativem Exponenten haben, können sie durch Faltung ihrer
Koeffizientenfolgen multipliziert werden, so wie es mit Potenzreihen gemacht
wird. Mit diesen Verknüpfungen wird die Menge aller Laurent-Reihen über einem
kommutativen Ring
zu einem kommutativen Ring, der mit
bezeichnet wird.
Ist
ein Körper,
dann bilden die formalen
Potenzreihen in der Unbestimmten
über
einen Integritätsring,
der mit
bezeichnet wird. Sein Quotientenkörper
ist isomorph zum Körper
der Laurent-Reihen über
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 30.12. 2020