Durchmesser

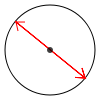
Die rote Linie bezeichnet man als Durchmesser

Der Durchmesser (griechisch διάμετρος, diámetros) eines Kreises oder einer Kugel ist der größtmögliche Abstand zweier Punkte der Kreislinie oder der Kugeloberflächenpunkte. Beim Kreis ist dies die längstmögliche Sehne. Der Durchmesser eines Rotationskörpers ist die längste Sehne senkrecht zur Rotationsachse des Körpers.

Geometrie

Der Durchmesser eines Kreises oder einer Kugel entspricht dem Abstand zwischen den Schnittpunkten mit einer Geraden, die durch den Mittelpunkt verläuft. Auch in höherdimensionalen Fällen ist der Durchmesser die Länge der Strecke, die aus einer Geraden durch den Mittelpunkt der Sphäre (des Kreises, der Kugel, der -Sphäre …) ausgeschnitten wird. Auch diese Strecke selbst wird gelegentlich als ein Durchmesser der Sphäre bezeichnet.

Die Hälfte eines Durchmessers wird Radius genannt. Das Verhältnis Umfang eines Kreises zum Durchmesser ist die Kreiszahl $\,\pi =3{,}14159\dots$ . Bei einem Kreis gilt daher

$d={\frac {U}{\pi }}=2r.$

Durchmesser in metrischen Räumen

Eine mathematische Verallgemeinerung ist der Durchmesser einer Menge in einem metrischen Raum . Er ist definiert als das Supremum aller Abstände je zweier Punkte des Raumes,

$\operatorname {diam}(M):=\sup\{d(x,y):x,y\in M\}$

Für Kreise und Kugeln in euklidischen Räumen stimmt diese Definition mit dem oben genannten geometrischen Begriff überein.

Technik

Technische Formeln werden bevorzugt so aufgebaut, dass der Durchmesser und nicht der Radius als Variable enthalten ist, da sich der Durchmesser mit den werkstattüblichen Messmitteln (z.B. Messschieber) direkt ermitteln und dann in der Formel anwenden lässt.

In der Metallverarbeitung kann zum Beispiel der Durchmesser einer Bohrung oder eines Bolzens mit dem geeigneten Messmittel gemessen werden. Der Durchmesser entspricht dabei dem größten Maß, das rechtwinklig zur Bohrungs- oder Bolzenachse gemessen wird.

Innen- und Außendurchmesser

Im Falle eines zylindrischen oder konischen Hohlkörpers mit ebenfalls zylindrischen oder konischen, meist zentrischen Durchbruch, Bohrung oder Einsenkung unterscheidet man zwischen dem inneren und äußeren Durchmesser. Als Beispiel seien Schläuche, Rohre, Hohlwellen, Kugellager und dergleichen genannt. Der Herstellungsprozess umfasst dabei fast alle in der Fertigungstechnik bekannten Verfahren, wobei die genauesten Ergebnisse weitestgehend vom Werkstoff und den Abmessungen des Werkstücks abhängen.

Für das Messen und Prüfen der Durchmesser wurden zum Teil spezielle Geräte und Messmethoden entwickelt. Für den Innendurchmesser gibt es unter anderem Innenmessschrauben oder Schnelltaster, zum Prüfen sind besonders die Lehrdorne erwähnenswert. Außendurchmesser lassen sich mit nahezu allen bekannten Längenmessmitteln messen, doch auch hierfür gibt es gesonderte Geräte. Die wohl bekanntesten sind der Messschieber, mit dem auch Innendurchmesser zu erfassen sind, und die Messschraube. Zum Prüfen eignen sich neben anderen Methoden vor allem Lehrringe. Ebenfalls beide Durchmesser, sofern sie nicht zu klein sind, können an modernen Koordinatenmessmaschinen erfasst werden.

Eine gesonderte Schreibweise für den Innen- oder Außendurchmesser konnte sich bis jetzt nicht durchsetzen, doch wird meist das kleine d für den Innendurchmesser und das große D für den Außendurchmesser verwendet. Bei Rohren und Schläuchen ist die Angabe der Abmessungen in der Regel durch den Außendurchmesser und die Wandstärke üblich und in einigen Bereichen auch genormt.

Durchmesserzeichen

In technischen Zeichnungen und Texten wird das Durchmesserzeichen ⌀ (U+2300) – nicht zu verwechseln mit dem Buchstaben ø bzw. Ø und dem Zeichen für die leere Menge ∅ (U+2205) – den Maßzahlen von Kreisformen vorangestellt. Früher wurde dies Zeichen nur dann verwendet, wenn die Kreisform nicht sofort erkennbar war, d.h. beispielsweise bei der Schnittdarstellung von Bohrungen oder Durchgangsbohrungen. In der Mathematik bezeichnet dieses Zeichen auch den Durchschnitt (Mittelwert).

Naturwissenschaften

Auch in den Naturwissenschaften, außer in der Astronomie, wird die Angabe eines Durchmessers häufig dem Radius vorgezogen, insbesondere dann, wenn das beschriebene Objekt nicht exakt kreis- bzw. kugelförmig ist.

In der Astronomie ist der Radius eine Messgröße für annähernd kugelförmige oder scheibenförmige Objekte, während der Durchmesser (als doppelter Wert des Radius) eher in populärwissenschaftlichen Texten angegeben ist.

→ Hauptartikel: Radius in der Astronomie

Weitere Begriffsverwendungen

Durchmesser (Graphentheorie) – der maximale Abstand zweier Knoten in einem Graphen
Äquivalentdurchmesser – der Durchmesser einer zu einem gegebenen Körper äquivalenten Kugel
- Aerodynamischer Durchmesser – Äquivalentdurchmesser bezüglich der Aerodynamik
Konjugierte Durchmesser – einander zugeordnete Durchmesser bei Kegelschnitten

Basierend auf einem Artikel in:

Wikipedia.de