Hypotenuse
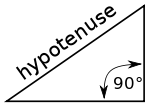
In der Geometrie ist eine Hypotenuse die längste Seite eines rechtwinkligen Dreiecks, das ist stets die dem rechten Winkel gegenüberliegende Seite. Die Länge der Hypotenuse eines rechtwinkligen Dreiecks kann mit dem Satz von Pythagoras ermittelt werden, der besagt, dass das Quadrat der Länge der Hypotenuse gleich der Summe der Quadrate der Längen der beiden anderen Seiten ist. Wenn zum Beispiel eine der Katheten eine Länge von 3 cm (im Quadrat 9 cm²) und die andere eine Länge von 4 cm (im Quadrat 16 cm²) hat, addieren sich ihre Quadrate zu 25 cm². Die Länge der Hypotenuse ist die Quadratwurzel von 25 cm², das sind 5 cm.
Etymologie
Das Wort Hypotenuse stammt aus dem Griechischen ἡ τὴν ὀρθὴν γωνίαν ὑποτείνουσα hē tḕn orthḕn gōnían hypoteínousa (sc. γραμμή grammḗ or πλευρά pleurá), dies bedeutet „Seite gegenüber dem rechten Winkel“ (Apollodorus). Das nominalisierte Partizip, ἡ ὑποτείνουσα hē hypoteínousa, wurde bis in das vierte Jahrhundert n.Chr. für die Hypotenuse des Dreiecks verwendet (belegt in Plato, Timaios 54d). Der griechische Begriff wurde in der Form hypotēnūsa ins Spätlateinische entlehnt. Die Schreibweise mit angehängtem -e als Hypotenuse ist französischen Ursprungs (Estienne de La Roche 1520).
Berechnung der Hypotenuse

Mit Hilfe von zwei vorgegebenen Längen oder einer Länge und einem spitzen Winkel kann die Länge der Hypotenuse berechnet werden.
Zwei Katheten
Nennt man bei einem rechtwinkligen Dreieck wie üblich die Länge der
Hypotenuse
und die Längen der Katheten
und
,
so gilt nach dem Satz
des Pythagoras:
Löst man das nach
auf, so erhält man (unter der Bedingung
)
die Formel
mit der man die Länge der Hypotenuse berechnen kann.
Kathete und Höhe
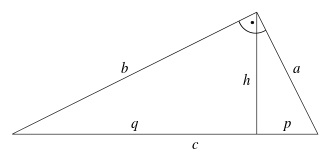
Die Höhe
teilt ein rechtwinkliges
Dreieck in zwei Teildreiecke. Der Fußpunkt der Höhe teilt die Hypotenuse
in die Hypotenusenabschnitte
und
.
Nach dem Satz des Pythagoras gilt
,
also
.
Das rechtwinklige Dreieck ist ähnlich
zu seinen Teildreiecken, weil die drei Innenwinkel
gleich sind. Deshalb stimmen entsprechende Seitenverhältnisse überein und es
gilt
,
also
und ebenso
Kathete und spitzer Winkel
Nach Definition von Sinus und Kosinus gilt:
Höhe und spitzer Winkel
Nach Definition von Tangens und Kotangens gilt für die Seiten und Winkel der Teildreiecke:
Daraus ergibt sich für die Länge der Hypotenuse
Viele Computersprachen
unterstützen die ISO-C-Standardfunktion hypot(x, y), die den obigen
Wert zurückgibt. Die Funktion ist so konzipiert, dass sie auch dann nicht
fehlschlägt, wenn die einfache Berechnung nach der Formel über- oder unterlaufen
kann, und ist auch oft etwas genauer.
Einige wissenschaftliche Taschenrechner
bieten eine Funktion zum Konvertieren von kartesischen
Koordinaten in Polarkoordinaten.
Diese gibt gleichzeitig sowohl die Länge der Hypotenuse als auch den Winkel aus, den die Hypotenuse
mit der Basislinie bildet, wenn
und
gegeben sind. Der zurückgegebene Winkel wird normalerweise durch
arctan2(y, x) angegeben.
Eigenschaften

- Die Höhe teilt ein rechtwinkliges Dreieck in zwei Teildreiecke. Das rechtwinklige Dreieck ist ähnlich zu seinen Teildreiecken, weil die drei Innenwinkel gleich sind (siehe Abbildung). Deshalb gelten folgende Seitenverhältnisse:
- Das Quadrat der Länge einer Kathete ist das Produkt der Länge seiner Orthogonalprojektion und der Länge der Hypotenuse.
- Also ist die Länge einer Kathete das geometrische Mittel zwischen der Länge seiner Orthogonalprojektion und der Länge der Hypotenuse.
Trigonometrische Funktionen
Mit Hilfe trigonometrischer
Funktionen kann man die Werte der beiden spitzen Winkel
und
des rechtwinkligen
Dreiecks berechnen.
Gegeben sind die Längen der Hypotenuse
und der Kathete
,
für deren Verhältnis gilt:
Die trigonometrische Umkehrfunktion ist
in der
der Winkel gegenüber der Kathete
ist. Der angrenzende Winkel der Kathete
ist
Man kann die Größe des Winkels
auch durch die Formel
berechnen, in der
die andere Kathete darstellt.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.05. 2021