Hyperbelfunktion

Sinus hyperbolicus (rot)
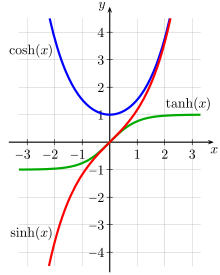
Kosinus hyperbolicus (blau)
Tangens hyperbolicus (grün)

Kosekans hyperbolicus (rot)
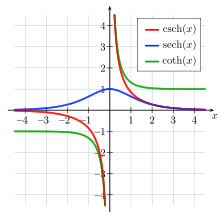
Sekans hyperbolicus (blau)
Kotangens hyperbolicus (grün)

Die Hyperbelfunktionen sind die korrespondierende Funktionen der trigonometrischen Funktionen (die auch als Winkel- oder Kreisfunktionen bezeichnet werden), allerdings nicht am Einheitskreis $x^{2}+y^{2}=1$ , sondern an der Einheitshyperbel $x^{2}-y^{2}=1$ .

Wie eng diese Funktionen miteinander verwandt sind, erschließt sich noch deutlicher in der komplexen Zahlenebene. Sie wird durch die Relation $(iy)^{2}=-y^{2}$ vermittelt. So gilt z. B. $\cos(ix)=\cosh x$ .

Folgende Funktionen gehören zu den Hyperbelfunktionen:

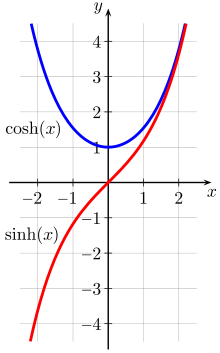
Hyperbelsinus oder lat. Sinus hyperbolicus (Formelzeichen: $\sinh$ )
Hyperbelkosinus oder lat. Cosinus hyperbolicus ( $\cosh$ )
Hyperbeltangens oder lat. Tangens hyperbolicus ( $\tanh$ )
Hyperbelkotangens oder lat. Cotangens hyperbolicus ( $\coth$ )
Hyperbelsekans oder lat. Sekans hyperbolicus ( $\operatorname {sech}$ )
Hyperbelkosekans oder lat. Kosekans hyperbolicus ( $\operatorname {csch}$ ).

In der deutschen und der holländischen Sprache werden noch sehr häufig die lateinischen Namen verwendet, mit teils eingedeutschter Schreibweise.

Sinus hyperbolicus und Kosinus hyperbolicus sind für alle komplexen Zahlen definiert und auf dem gesamten Gebiet der komplexen Zahlen holomorph. Die übrigen Hyperbelfunktionen haben Pole auf der imaginären Achse.

Definition

Eine Gerade aus dem Ursprung schneidet die Hyperbel $x^{2}-y^{2}=1$ im Punkt $(\cosh A,\sinh A)$ , wobei die Fläche zwischen der Geraden, ihrem Spiegelbild an der -Achse, und der Hyperbel ist.

Definition über die Exponentialfunktion

Mittels der Exponentialfunktion können $\sinh$ und $\cosh$ wie folgt definiert werden:

$\sinh(z):={\frac {e^{z}-e^{-z}}{2}}$

$\cosh(z):={\frac {e^{z}+e^{-z}}{2}}$

Daher sind die hyperbolischen Funktionen periodisch (mit rein imaginärer Periode). Die Potenzreihen von $\cosh$ und $\sinh$ lauten

${\begin{aligned}\sinh(z)&=z+{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}+{\frac {z^{7}}{7!}}+\dots =\sum _{n=0}^{\infty }{\frac {z^{2n+1}}{(2n+1)!}}\\\cosh(z)&=1+{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}+{\frac {z^{6}}{6!}}+\dots =\sum _{n=0}^{\infty }{\frac {z^{2n}}{(2n)!}}\,,\end{aligned}}$

wobei der Ausdruck für die Fakultät von , das Produkt der ersten natürlichen Zahlen steht. Im Gegensatz zu den Potenzreihenentwicklungen von $\cos$ und $\sin$ haben alle Terme ein positives Vorzeichen.

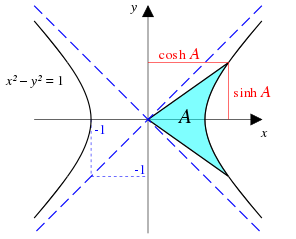
Geometrische Definition mit Hilfe der Hyperbel

Wegen ihrer Verwendung zur Parametrisierung der Einheitshyperbel $x^{2}-y^{2}=1$ :

$x=\cosh(t),y=\sinh(t)$

werden sie Hyperbelfunktionen genannt, in Analogie zu den Kreisfunktionen Sinus und Kosinus, die den Einheitskreis $x^{2}+y^{2}=1$ parametrisieren:

$x=\cos(t),y=\sin(t)$

Die Funktionen stellen eine Verbindung her zwischen der Fläche , die von einer vom Nullpunkt ausgehenden Geraden und ihrem Spiegelbild an der -Achse sowie der Hyperbel eingeschlossen wird, und der Länge verschiedener Strecken.

Dabei ist $\sinh(A)$ die (positive) -Koordinate des Schnittpunkts der Geraden mit der Hyperbel und $\cosh(A)$ die dazugehörige -Koordinate; $\tanh(A)$ ist die -Koordinate der Geraden bei x=1 , d.h. die Steigung der Geraden.

Berechnet man die Fläche durch Integration, erhält man die Darstellung mit Hilfe der Exponentialfunktion.

Eigenschaften der reellen Hyperbelfunktionen

Graph der reellen Hyperbelfunktionen

Für alle reellen Zahlen sind auch $\sinh(x)$ und $\cosh(x)$ reell.
Die reelle Funktion $\sinh$ ist streng monoton steigend und besitzt in ihren einzigen Wendepunkt.
Die reelle Funktion $\cosh$ ist für auf dem Intervall $(-\infty ,0]$ streng monoton fallend, auf dem Intervall $[0,\infty )$ streng monoton steigend und besitzt bei ein globales Minimum.

Wegen $\sinh ,\cosh \colon \mathbb {R} \mapsto \mathbb {R}$ gelten alle Eigenschaften der komplexen Hyperbelfunktionen, die im nachfolgenden Absatz aufgeführt sind, auch für die Funktionen, die auf die reellen Zahlen eingeschränkt sind.

Eigenschaften der komplexen Hyperbelfunktionen

Für alle komplexen Zahlen $z,z_{1},z_{2}$ gilt:

Symmetrie und Periodizität

$\sinh(z)=-\sinh(-z)$ , d.h., sinh ist eine ungerade Funktion.
$\cosh(z)=\cosh(-z)$ , d.h., cosh ist eine gerade Funktion.

$\sinh(z)=\sinh(z+2\pi i)\quad {\text{ und }}\quad \cosh(z)=\cosh(z+2\pi i)$ ,

d.h., es liegt rein „imaginäre Periodizität“ vor mit minimaler Periodenlänge $2\pi$ .

Additionstheoreme

$\sinh(z_{1}\pm z_{2})=\sinh(z_{1})\cdot \cosh(z_{2})\pm \sinh(z_{2})\cdot \cosh(z_{1})$
$\cosh(z_{1}\pm z_{2})=\cosh(z_{1})\cdot \cosh(z_{2})\pm \sinh(z_{1})\cdot \sinh(z_{2})$
$\tanh(z_{1}\pm z_{2})={\frac {\tanh(z_{1})\pm \tanh(z_{2})}{1\pm \tanh(z_{1})\tanh(z_{2})}}$

Zusammenhänge

${\cosh }^{2}(z)-{\sinh }^{2}(z)=1$

$\cosh z+\sinh z\ =e^{z}$

$\cosh z-\sinh z\ =e^{-z}$

Ableitung

Die Ableitung des Sinus hyperbolicus lautet:

${\frac {\mathrm {d} }{\mathrm {d} z}}{\sinh }(z)=\cosh(z)$ .

Die Ableitung des Kosinus hyperbolicus lautet:

${\frac {\mathrm {d} }{\mathrm {d} z}}{\cosh }(z)=\sinh(z)$ .

Die Ableitung des Tangens hyperbolicus lautet:

${\frac {\mathrm {d} }{\mathrm {d} z}}{\tanh }(z)=1-{\tanh }^{2}(z)={\frac {1}{\cosh ^{2}(z)}}$ .

Differentialgleichung

Die Funktionen $\sinh(z)$ und $\cosh(z)$ bilden wie $e^{z}$ und $e^{{-z}}$ eine Lösungsbasis (Fundamentalsystem) der linearen Differentialgleichung

${\frac {\mathrm {d} ^{2}}{\mathrm {d} z^{2}}}f(z)=f(z)$ .

Fordert man allgemein für die beiden Basislösungen $f_{i}(z)$ dieser Differentialgleichung zweiter Ordnung noch $f_{1}(0)=0$ , $f_{1}'(0)=1$ und $f_{2}(0)=1$ , $f_{2}'(0)=0$ , so sind sie bereits eindeutig durch $\sinh$ und $\cosh$ festgelegt. Sprich, diese Eigenschaft kann ebenfalls als Definition dieser beiden Hyperbelfunktionen herangezogen werden.

Bijektivität der komplexen Hyperbelfunktionen

sinh

Es seien folgende Teilmengen der komplexen Zahlen definiert:

$A:=\{z\in \mathbb {C} \mid -\pi /2<\operatorname {Im} \,z<\pi /2\}$

$B:=\{z\in \mathbb {C} \mid \operatorname {Re} \,z\neq 0\vee |\operatorname {Im} \,z|<1\}$

Dann bildet die komplexe Funktion $\sinh$ den „Streifen“ bijektiv auf ab.

cosh

Es seien folgende Teilmengen der komplexen Zahlen definiert:

$A:=\{z\in \mathbb {C} \mid 0<\operatorname {Im} \,z<\pi \}$

$B:=\{z\in \mathbb {C} \mid \operatorname {Im} \,z\neq 0\vee |\operatorname {Re} \,z|<1\}$

Dann bildet die komplexe Funktion $\cosh$ den „Streifen“ bijektiv auf ab.

Historische Notation

In deutschsprachiger Literatur wurden zur Unterscheidung von den trigonometrischen Funktionen die Hyperbelfunktionen lange Zeit in Frakturschrift dargestellt – mit initialer Großschreibung und ohne abschließendes h:

${\mathfrak {Sin}}\,x\,{\widehat {=}}\,\sinh x$

${\mathfrak {Cos}}\,x\,{\widehat {=}}\,\cosh x$

${\mathfrak {Tan}}\,x\ /\ {\mathfrak {Tg}}\,x\,{\widehat {=}}\,\tanh x\ /\ \operatorname {tgh} x$

${\mathfrak {Cot}}\,x\ /\ {\mathfrak {Ctg}}\,x\,{\widehat {=}}\,\coth x\ /\ \operatorname {ctgh} x$

${\mathfrak {Sec}}\,x\,{\widehat {=}}\,\operatorname {sech} x$

${\mathfrak {Csc}}\,x\,{\widehat {=}}\,\operatorname {csch} x$

Alternative Namen

Für die Hyperbelfunktionen ist auch der Name hyperbolische Funktionen gebräuchlich.
Für $\sinh$ sind auch die Namen hsin, Hyperbelsinus und Sinus hyperbolicus gebräuchlich.
Für $\cosh$ sind auch die Namen hcos, Hyperbelcosinus und Cosinus hyperbolicus gebräuchlich. Der Graph entspricht der Kettenlinie (Katenoide).

Abgeleitete Funktionen

Tangens hyperbolicus: $\tanh(x):={\frac {\sinh(x)}{\cosh(x)}}$
Cotangens hyperbolicus: $\coth(x):={\frac {1}{\tanh(x)}}={\frac {\cosh(x)}{\sinh(x)}}$
Secans hyperbolicus: $\operatorname {sech} (x):={\frac {1}{\cosh(x)}}$
Kosecans hyperbolicus: $\operatorname {csch} (x):={\frac {1}{\sinh(x)}}$

Umrechnungstabelle

Funktion	$\sinh$	$\cosh$	$\tanh$	$\coth$	$\operatorname {sech}$	$\operatorname {csch}$
$\sinh(x)=$	$\sinh(x)\,$	$\operatorname {sgn}(x){\sqrt {\cosh ^{2}(x)-1}}$	${\frac {\tanh(x)}{\sqrt {1-\tanh ^{2}(x)}}}$	${\frac {\operatorname {sgn}(x)}{\sqrt {\coth ^{2}(x)-1}}}$	$\operatorname {sgn}(x){\frac {\sqrt {1-\operatorname {sech} ^{2}(x)}}{\operatorname {sech} (x)}}$	${\frac {1}{\operatorname {csch} (x)}}$
$\cosh(x)=$	$\,{\sqrt {1+\sinh ^{2}(x)}}$	$\,\cosh(x)$	$\,{\frac {1}{\sqrt {1-\tanh ^{2}(x)}}}$	$\,{\frac {\left\|\coth(x)\right\|}{\sqrt {\coth ^{2}(x)-1}}}$	$\,{\frac {1}{\operatorname {sech} (x)}}$	$\,{\frac {\sqrt {1+\operatorname {csch} ^{2}(x)}}{\left\|\operatorname {csch} (x)\right\|}}$
$\tanh(x)=$	$\,{\frac {\sinh(x)}{\sqrt {1+\sinh ^{2}(x)}}}$	$\,\operatorname {sgn}(x){\frac {\sqrt {\cosh ^{2}(x)-1}}{\cosh(x)}}$	$\,\tanh(x)$	$\,{\frac {1}{\coth(x)}}$	$\,\operatorname {sgn}(x){\sqrt {1-\operatorname {sech} ^{2}(x)}}$	$\,{\frac {\operatorname {sgn}(x)}{\sqrt {1+\operatorname {csch} ^{2}(x)}}}$
$\coth(x)=$	$\,{\frac {\sqrt {1+\sinh ^{2}(x)}}{\sinh(x)}}$	$\,\operatorname {sgn}(x){\frac {\cosh(x)}{\sqrt {\cosh ^{2}(x)-1}}}$	$\,{\frac {1}{\tanh(x)}}$	$\,\coth(x)$	$\,{\frac {\operatorname {sgn}(x)}{\sqrt {1-\operatorname {sech} ^{2}(x)}}}$	$\,\operatorname {sgn}(x){\sqrt {1+\operatorname {csch} ^{2}(x)}}$
$\operatorname {sech} (x)=$	$\,{\frac {1}{\sqrt {1+\sinh ^{2}(x)}}}$	$\,{\frac {1}{\cosh(x)}}$	$\,{\sqrt {1-\tanh ^{2}(x)}}$	$\,{\frac {\sqrt {\coth ^{2}(x)-1}}{\left\|\coth(x)\right\|}}$	$\,\operatorname {sech} (x)$	$\,{\frac {\left\|\operatorname {csch} (x)\right\|}{\sqrt {1+\operatorname {csch} ^{2}(x)}}}$
$\operatorname {csch} (x)=$	$\,{\frac {1}{\sinh(x)}}$	$\,{\frac {\operatorname {sgn}(x)}{\sqrt {\cosh ^{2}(x)-1}}}$	$\,{\frac {\sqrt {1-\tanh ^{2}(x)}}{\tanh(x)}}$	$\,\operatorname {sgn}(x){\sqrt {\coth ^{2}(x)-1}}$	$\,\operatorname {sgn}(x){\frac {\operatorname {sech} (x)}{\sqrt {1-\operatorname {sech} ^{2}(x)}}}$	$\,\operatorname {csch} (x)$