Extremwert

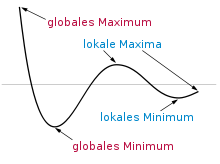
Minima und Maxima der Funktion cos(3πx)/x im Bereich 0.1≤ x ≤1.1

In der Mathematik ist Extremwert (oder Extremum; Plural: Extrema) der Oberbegriff für ein lokales oder globales Maximum oder Minimum. Ein lokales Maximum bzw. lokales Minimum ist der Wert der Funktion an einer Stelle , wenn in einer hinreichend kleinen Umgebung die Funktion keine größeren bzw. kleineren Werte annimmt; die zugehörige Stelle wird lokaler Maximierer bzw. lokaler Minimierer, Maximalstelle bzw. Minimalstelle oder zusammenfassend auch Extremstelle genannt, die Kombination aus Stelle und Wert Extrempunkt.

Ein globales Maximum wird auch absolutes Maximum genannt, für ein lokales Maximum wird auch der Begriff relatives Maximum gebraucht. Lokale und globale Minima sind analog definiert.

Die Lösung einer Extremwertaufgabe nennt man die extremale Lösung.

Eindimensionaler Fall

Formale Definition

Es sei $U\subseteq\mathbb R$ eine Teilmenge der reellen Zahlen (z.B. ein Intervall) und $f\colon U\to\mathbb R$ eine Funktion.

hat an der Stelle $x_{0}\in U$

ein lokales Minimum, wenn es ein Intervall gibt, das $x_{0}$ enthält, so dass $f(x_{0})\leq f(x)$ für alle $x\in I\cap U$ gilt;
ein globales Minimum, wenn $f(x_{0})\leq f(x)$ für alle $x\in U$ gilt;
ein lokales Maximum, wenn es ein Intervall gibt, das $x_{0}$ enthält, so dass $f(x_{0})\geq f(x)$ für alle $x\in I\cap U$ gilt;
ein globales Maximum, wenn $f(x_{0})\geq f(x)$ für alle $x\in U$ gilt.

Besitzt die Funktion an der Stelle $x_{0}$ ein Maximum, so nennt man den Punkt $(x_{0},f(x_{0}))$ Hochpunkt, hat sie dort ein Minimum, so heißt der Punkt Tiefpunkt. Liegt ein Hoch- oder ein Tiefpunkt vor, so spricht man von einem Extrempunkt.

Existenz von Extrema

Sind $a \le b$ reelle Zahlen und ist $f\colon [a,b]\to \mathbb {R}$ eine stetige Funktion, so nimmt ein globales Maximum und ein globales Minimum an. Diese können auch in den Randstellen oder angenommen werden.

Diese Aussage folgt aus dem Satz von Heine-Borel, wird aber oft auch nach K. Weierstraß oder B. Bolzano benannt oder als Satz vom Maximum und Minimum bezeichnet.

Bestimmung von Extremstellen differenzierbarer Funktionen

Es sei $U\subseteq\mathbb R$ offen, und $f\colon U\to\mathbb R$ eine differenzierbare Funktion.

Notwendiges Kriterium

Hat an einer Stelle $x_{0}\in U$ ein lokales Extremum und ist dort differenzierbar, so ist dort die erste Ableitung gleich null:

$f'(x_{0})=0\,$ .

Hinreichende Kriterien

Ist zweimal differenzierbar, und gilt neben $f'(x_{0})=0\,$ auch $f''(x_{0})\neq 0\,$ , so hat an der Stelle $x_{0}$ ein lokales Extremum. Ist $f'(x_{0})=0\,$ und $f''(x_{0})>0\,$ , handelt es sich dabei um ein lokales Minimum, für $f''(x_{0})<0\,$ dagegen um ein lokales Maximum.

Allgemeiner dagegen und mittels Entwicklung von gemäß der Taylor-Formel herleitbar gilt: Ist n-mal ableitbar und dabei

$f'(x_{0})=f''(x_{0})=\ldots =f^{(n-1)}(x_{0})=0\,\wedge f^{(n)}(x_{0})\neq 0,$

so folgt daraus:

(1) Ist gerade sowie $f^{(n)}(x_{0})<0$ (bzw. $f^{(n)}(x_{0})>0$ ), so hat damit bei $x_{0}$ ein relatives Maximum (bzw. Minimum).

(2) Ist hingegen ungerade, so hat bei $x_{0}$ kein lokales Extremum (des Funktionswerts, sondern eines des Anstiegs, also eine Wendestelle).

Oder ganz allgemein formuliert: Ist die erste von Null verschiedene Ableitung $f^{(n)}$ der Funktion an der Stelle $x_{0}$ , an der $f'(x_{0})=0$ ist, eine Ableitung gerader Ordnung, so besitzt damit an dieser Stelle einen Extrempunkt, wobei eine von Null verschiedene Ableitung $f^{(n)}>0$ für ein Minimum, eine Ableitung $f^{(n)}<0$ dagegen für ein Maximum steht. (Man vergleiche hierzu Funktionen der Form: f(x)=x^n

, $n\in \mathbb {N}$ .)

Hat die erste Ableitung bei $x_{0}$ einen Vorzeichenwechsel, so liegt ein Extremum vor. Bei einem Vorzeichenwechsel von Plus nach Minus handelt es sich um ein Maximum, bei einem Vorzeichenwechsel von Minus nach Plus um ein Minimum.

Für stetige Funktionen auf Intervallen gilt: Zwischen zwei lokalen Minima einer Funktion liegt stets ein lokales Maximum, und zwischen zwei lokalen Maxima liegt stets ein lokales Minimum.

Für differenzierbare Funktionen auf Intervallen gilt: Gibt es zwei Stellen mit $a<x_{0}<b$ , so dass die erste Ableitung im Intervall nur die Nullstelle $x_{0}$ hat, und ist $f(a)>f(x_{0})$ sowie $f(b)>f(x_{0})$ , so hat bei $x_{0}$ ein lokales Minimum. Gilt die analoge Bedingung mit $f(a)<f(x_{0})$ und $f(b)<f(x_{0})$ , so hat bei $x_{0}$ ein lokales Maximum.

Es gibt allerdings auch Funktionen, bei denen keines der og. Kriterien weiterhilft (s.u.).

Beispiele

$f(x)=x^{2}+3.$ Die erste Ableitung hat nur bei $x_{0}=0$ eine Nullstelle. Die zweite Ableitung ist dort positiv, also nimmt bei 0 ein lokales Minimum an, nämlich .

Die erste Ableitung hat nur bei eine Nullstelle. Die zweite Ableitung ist dort ebenfalls 0. Man kann nun auf verschiedene Arten fortfahren:
- Auch die dritte Ableitung ist dort 0. Die vierte Ableitung hingegen ist mit $f^{{(4)}}(x)=24$ die erste höhere Ableitung, die nicht 0 ist. Da diese Ableitung einen positiven Wert hat und gerade ist, gilt nach (1), dass die Funktion dort ein lokales Minimum besitzt.
- Die erste Ableitung hat bei 0 einen Vorzeichenwechsel von Minus nach Plus, also hat bei $x_{0}=0$ ein lokales Minimum.
- Es ist , also hat im Intervall ein lokales Minimum. Da die erste Ableitung in diesem Intervall nur die Nullstelle $x_{0}=0$ hat, muss das lokale Minimum dort angenommen werden.

Die Funktion, die durch für und durch definiert ist, hat die folgenden Eigenschaften:
- Sie hat bei ein globales Minimum.
- Sie ist beliebig oft differenzierbar.
- Alle Ableitungen bei sind gleich 0.
- Die erste Ableitung hat keinen Vorzeichenwechsel bei 0.
- Auch die anderen beiden oben genannten Kriterien sind nicht anwendbar.

Anwendungsbeispiel

In der Praxis können Extremwert-Berechnungen zur Berechnung von größt- oder kleinstmöglichen Vorgaben verwendet werden, wie das folgende Beispiel zeigt (siehe auch Optimierungsproblem):

Wie muss eine rechteckige Fläche aussehen, die bei einem bestimmten Umfang eine maximale Fläche hat?

Lösungsweg:

Der Umfang ist konstant, die Fläche soll maximiert werden, ist die Länge und die Breite:

$1)\qquad U=2(a+b)\Rightarrow b={\frac {U}{2}}-a$

$2)\qquad A=a\cdot b$

1) in 2) einsetzen und umformen

$A(a)=-a^{2}+{\frac {1}{2}}Ua$

Ableitungsfunktionen bilden

$A'(a)=-2a+{\frac {1}{2}}U$

$A''(a)=-2\qquad \Rightarrow$ Hochpunkt der Funktion

Es gibt nur ein lokales Maximum, das in dem vorliegenden Beispiel (ohne Nachweis) zugleich auch das globale Maximum ist, da die zweite Ableitung unabhängig von der Variablen immer kleiner als Null ist.

Um einen Extremwert zu finden, muss die erste Ableitung gleich Null gesetzt werden (da diese die Steigung der ursprünglichen Funktion beschreibt und diese Steigung bei Extremwerten Null ist. Ist die zweite Ableitung der Funktion ungleich Null, so liegt ein Minimum oder Maximum vor).

$A'(a)=-2a+{\frac {1}{2}}U=0\Rightarrow$

$a={\frac {1}{4}}U\ \Rightarrow \ U=4a$

Einsetzen in 1)

$4a=2(a+b)\ \Rightarrow \ a=b$

Es folgt daraus, dass der größtmögliche Flächeninhalt eines Rechtecks bei vorgegebenen Umfang dann zu erzielen ist, wenn beide Seitenlängen gleich sind (was einem Quadrat entspricht). Umgekehrt lässt sich aber auch sagen, dass ein Rechteck mit vorgegebenem Flächeninhalt den geringsten Umfang aufweist, wenn sich

verhalten – also bei einem Quadrat.

Mehrdimensionaler Fall

Es sei $U\subseteq\mathbb R^n$ und $f\colon U\to\mathbb R$ eine Funktion. Weiterhin sei ein innerer Punkt von . Ein lokales Minimum/Maximum in ist dann gegeben, wenn eine Umgebung um existiert, in welcher kein Punkt einen kleineren bzw. größeren Funktionswert annimmt.

Analog zum eindimensionalen Fall ist das Verschwinden des Gradienten

$Df(x)=\operatorname{grad} f(x)$

eine notwendige Bedingung dafür, dass im Punkt ein Extremum annimmt. Hinreichend ist in diesem Fall die Definitheit der Hesse-Matrix $D^{2}f(x)$ : ist sie positiv definit, liegt ein lokales Minimum vor; ist sie negativ definit, handelt es sich um ein lokales Maximum; ist sie indefinit, liegt kein Extrempunkt, sondern ein Sattelpunkt vor. Wenn sie nur semidefinit ist, ist keine Entscheidung anhand der Hesse-Matrix möglich (peanosche Fläche).

Unendlichdimensionaler Fall

Definition

Der Begriff des Maximums und des Minimums überträgt sich direkt auf den unendlichdimensionalen Fall. Ist ein Vektorraum und $D\subset X$ eine Teilmenge dieses Vektorraumes sowie $f\colon D \to \R$ ein Funktional. Dann hat an der Stelle ${\tilde x}\in D$

ein (globales) Minimum, wenn $f({\tilde x})\leq f(x)$ für alle $x \in D$
ein (globales) Maximum, wenn $f({\tilde x})\geq f(x)$ für alle $x \in D$

Der Zusatz „globales“ wird meist weggelassen, wenn aus dem Zusammenhang klar ist, was gemeint ist. Ist zusätzlich mit einer Topologie versehen, also ein topologischer Raum, dann hat an der Stelle ${\tilde x}\in D$

ein lokales Minimum, wenn es eine Umgebung von $\tilde x$ gibt, so dass $f({\tilde x})\leq f(x)$ für alle $x\in U\cap D$ gilt.
ein lokales Maximum, wenn es eine Umgebung von $\tilde x$ gibt, so dass $f({\tilde x})\geq f(x)$ für alle $x\in U\cap D$ gilt.

Ein Punkt heißt ein (lokales) Extremum, wenn er ein (lokales) Minimum oder ein (lokales) Maximum ist. Jedes globale Minimum (Maximum) ist ein lokales Minimum (Maximum).

Existenz, Eindeutigkeit und Geometrie von Extrema

Existenz

Entsprechend den Existenzaussagen für reelle Funktionen gibt es auch Aussagen für die Existenz von Extremalstellen von Funktionalen. Ist ein normierter Raum, so gilt:

Ein schwach unterhalbstetiges Funktional auf einer schwach folgenkompakten Menge nimmt dort ihr Minimum an.

Da diese Version für die Anwendung und Überprüfung oft unpraktisch ist, schwächt man dies ab zu der Aussage, dass jedes stetige quasikonvexe Funktional auf einer beschränkten, konvexen und abgeschlossenen Teilmenge eines reflexiven Banachraums ein Minimum annimmt. Diese Aussage gilt auch für alle konvexen Funktionale, da diese immer quasikonvex sind. Im Endlichdimensionalen kann auf die Konvexität der Teilmenge verzichtet werden.

Eindeutigkeit

Unter gewissen Umständen sind die Optimalpunkte sogar eindeutig bestimmt. Dazu gehört zum Beispiel die strikte Konvexität.

Geometrie

Schränkt man sich auf gewisse Klassen von Funktionalen ein, so kann man Aussagen über die Geometrie der Menge der Extremalpunkte treffen.

Ist das Funktional quasikonvex auf einer konvexen Menge, so ist die Menge der Minima konvex.
Ist das Funktional quasikonkav auf einer konvexen Menge, so ist die Menge der Maxima konvex.
Ist das Funktional konvex auf einer konvexen Menge, so ist jedes lokale Minimum ein globales Minimum.
Ist das Funktional konkav auf einer konvexen Menge, so ist jedes lokale Maximum ein globales Maximum.

Andere Extremwerte

Diskrete Optimierung

Bei diskreten Optimierungsproblemen ist der oben definierte Begriff des lokalen Extremums nicht geeignet, da in jedem Punkt ein lokales Extremum in diesem Sinne vorliegt. Für Extrema einer Funktion $f\colon D\to {\mathbb R}$ wird daher ein anderer Umgebungsbegriff verwendet: Man benutzt eine Nachbarschaftsfunktion , die jedem Punkt die Menge seiner Nachbarn zuordnet,

$N\colon D\to {\mathcal P}(D);$

dabei steht ${\mathcal P}(D)$ für die Potenzmenge von .

hat dann ein lokales Maximum in einem Punkt $x_{0}\in D$ , wenn $f(x)\leq f(x_{0})$ für alle Nachbarn $x\in N(x_{0})$ gilt. Lokale Minima sind analog definiert.

Variationsrechnung

Extremwerte von Funktionen, deren Argumente selbst Funktionen sind, z.B. die Kontur eines Regentropfens mit minimalem Luftwiderstand, sind Gegenstand der Variationsrechnung.

Siehe auch

Maximumprinzip

Basierend auf einem Artikel in:

Wikipedia.de