Zusammenhängender Raum

Zusammenhängende und nicht zusammenhängende Unterräume von R² : A ist einfach zusammenhängend, B (das gesamte Blaue) sowie die Komplemente von A und B sind es nicht.

In der mathematischen Topologie gibt es verschiedene Begriffe, die die Art und Weise des Zusammenhangs eines topologischen Raumes beschreiben. Im Allgemeinen heißt ein topologischer Raum X zusammenhängend, falls es nicht möglich ist, ihn in zwei disjunkte, nichtleere, offene Teilmengen aufzuteilen. Ein Teilraum eines topologischen Raumes heißt zusammenhängend, wenn er unter der induzierten Topologie zusammenhängend ist.

Eine maximale zusammenhängende Teilmenge eines topologischen Raumes heißt Zusammenhangskomponente.

Formale Definition

Für einen topologischen Raum $\big( X,\mathcal O\big)$ sind folgende Aussagen äquivalent:

ist zusammenhängend.
kann nicht in zwei disjunkte nichtleere offene Mengen zerlegt werden:

$\forall O_1, O_2 \in \mathcal{O}, O_1 \neq \emptyset, O_2 \neq \emptyset: O_1 \cap O_2 = \emptyset\Rightarrow O_1 \cup O_2 \neq X$
kann nicht in zwei disjunkte nichtleere abgeschlossene Mengen zerlegt werden:

$\forall O_1, O_2 \in \mathcal{O}, O_1 \neq \emptyset, O_2 \neq \emptyset: (X \setminus O_1) \cap (X \setminus O_2) = \emptyset\Rightarrow (X \setminus O_1) \cup (X \setminus O_2) \neq X$
und $\emptyset$ sind die beiden einzigen Mengen, die zugleich offen und abgeschlossen sind.
Die einzigen Mengen mit leerem Rand sind und $\emptyset$ .
kann nicht als Vereinigung zweier nichtleerer getrennter Mengen geschrieben werden.
Jede stetige Abbildung von in einen diskreten topologischen Raum ist konstant.
Jede lokal konstante Funktion von in eine beliebige Menge ist konstant.

Eine Teilmenge eines topologischen Raumes nennt man zusammenhängend, wenn sie in der Teilraumtopologie zusammenhängend ist; siehe im Beispiel:

Beispiel

Sei $X:= \left[0,1\right[\cup\left[3,4\right[\subseteq \mathbb{R}$ . In Worten ist also die disjunkte Vereinigung von zwei Intervallen. Diese Menge ist wie üblich mit der von $\mathbb{R}$ induzierten Topologie (Teilraumtopologie, Spurtopologie) versehen. Dies bedeutet, dass die in X offenen Mengen gerade die Mengen von der Form $V\cap X$ sind, wobei eine in $\mathbb{R}$ offene Menge ist. Eine Menge ist also genau dann in X offen, wenn sie sich als Schnitt einer in $\mathbb{R}$ offenen Menge mit X schreiben lässt.

Das Intervall $V_1:=\left]-1,2\right[$ ist in $\mathbb{R}$ offen. Also ist der Schnitt von V_1 mit in X offen. Dies ergibt gerade [0,1[ . Also ist die Menge [0,1[ in X offen, obwohl [0,1[ natürlich nicht in $\mathbb{R}$ offen ist.

Ebenso ist das Intervall $V_2:=\left]2,5\right[$ in $\mathbb{R}$ offen. Also ist der Schnitt von V_2 mit unserem Raum in X offen. Dieser Schnitt ist nun gerade die Menge [3,4[ . Also ist [3,4[ eine offene Teilmenge des Raumes .

Damit kann man den Raum als disjunkte Vereinigung von zwei in X offenen Teilmengen schreiben, die beide nicht leer sind. Also ist nicht zusammenhängend.

Dies lässt sich alternativ auch folgendermaßen sehen: Das Intervall [0,2] ist in $\mathbb{R}$ abgeschlossen. Also ist $[0,2]\cap X$ in X abgeschlossen. Dieser Schnitt ist die Menge [0,1[ , also ist [0,1[ in X abgeschlossen, obwohl [0,1[ nicht in $\mathbb{R}$ abgeschlossen ist.

Da wie oben erläutert [0,1[ in X auch offen ist, existiert mit [0,1[ eine Teilmenge von , die gleichzeitig sowohl offen als auch abgeschlossen (in X) ist, aber nicht leer ist und auch nicht ganz . Also kann nicht zusammenhängend sein.

Globale Zusammenhangsbegriffe

Die folgenden Begriffe beziehen sich immer auf den ganzen Raum, sind also globale Eigenschaften:

Total unzusammenhängend

→ Hauptartikel: Total unzusammenhängender Raum

Ein Raum ist total unzusammenhängend, falls er keine zusammenhängende Teilmenge mit mehr als einem Punkt besitzt, wenn also alle Zusammenhangskomponenten einpunktig sind. Jeder diskrete topologische Raum ist total unzusammenhängend. In diesem Fall sind die (einpunktigen) Zusammenhangskomponenten offen. Ein Beispiel für einen nicht diskreten total unzusammenhängenden Raum ist die Menge der rationalen Zahlen $\mathbb Q$ mit der von $\mathbb R$ induzierten Topologie.

Wegzusammenhängend

Dieser Unterraum von R² ist wegzusammenhängend, da je zwei seiner Punkte durch einen Weg verbunden sind.

Dieser Unterraum von R² ist zwar zusammenhängend, doch nicht wegzusammenhängend.

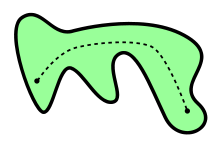
Ein topologischer Raum ist wegzusammenhängend (oder pfad-zusammenhängend oder kurvenweise zusammenhängend), falls es für jedes Paar von Punkten , aus einen Weg von nach gibt, d.h. eine stetige Abbildung $p\colon [0,1] \to X$ mit p(0) = x und p(1) = y .

Wegzusammenhängende Räume sind immer zusammenhängend. Etwas überraschend ist auf den ersten Blick jedoch vielleicht, dass es Räume gibt, die zusammenhängend, aber nicht wegzusammenhängend sind. Ein Beispiel ist die Vereinigung des Graphen von

$(0,\infty) \to \mathbb R, \quad x\mapsto \sin (1/x)$

mit einem Abschnitt der -Achse zwischen −1 und 1, mit der von $\mathbb R^2$ induzierten Topologie. Da in jeder Umgebung der Null auch ein Stück des Graphen liegt, kann man die -Achse nicht vom Graphen als eine offene Teilmenge abtrennen; die Menge ist also zusammenhängend. Andererseits gibt es keinen Weg von einem Punkt auf dem Graphen zu einem Punkt auf der -Achse, also ist diese Vereinigung nicht wegzusammenhängend.

Einfach zusammenhängend

Zusammenhängende und nicht zusammenhängende Unterräume von R² : C und sein Komplement sind einfach zusammenhängend, D und sein Komplement dagegen nicht.

Ein Raum ist einfach zusammenhängend, falls er wegzusammenhängend ist und sich jeder geschlossene Weg auf einen Punkt zusammenziehen lässt, d.h. nullhomotop ist. Die zweite Bedingung ist dazu äquivalent, dass die Fundamentalgruppe trivial ist.

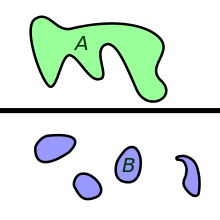
So sind in der nebenstehenden Abbildung sowohl der pinkfarbene Raum C als auch sein weißes Komplement „einfach zusammenhängend“, ersterer allerdings erst dadurch, dass eine Trennlinie die Umrundung des weiß gezeichneten Komplements verhindert. Im unteren Teilbild dagegen sind weder der orangefarbene Raum D noch sein weiß gezeichnetes Komplement „einfach zusammenhängend“ – interpretiert man D als Darstellung der Topologie einer „Kugel mit vier Henkeln“, wären das Komplement die vier „Löcher“ der Henkelkugel.

Im Unterschied zu Teilräumen des $\mathbb R^2$ , die, sobald sie einen oder mehrere nicht zu dem Raum gehörende Punkte („Löcher“) enthalten, dadurch auch nicht mehr „einfach zusammenhängend“ sind, gilt dies für Teilräume des $\mathbb R^3$ zunächst einmal nicht: Ein Raum mit der Topologie eines (ganzen) Schweizer Käses etwa bleibt dennoch (und unabhängig von der Zahl der Löcher in seinem Inneren) „einfach zusammenhängend“, weil jeder geschlossene Weg in einem solchen Raum sich unter Umgehung der Löcher zu einem Punkt zusammenziehen lässt. Wird der Raum dagegen von einer Kurve, z.B. einer Geraden, komplett durchquert, deren Punkte allesamt nicht zu dem Raum gehören, entsteht die Situation des Volltorus: Ein sich um die Gerade schließender Weg kann damit nicht mehr auf einen einzelnen Punkt zusammengezogen werden.

n-zusammenhängend

Ist eine nichtnegative ganze Zahl, so heißt ein topologischer Raum -zusammenhängend, falls alle Homotopiegruppen $\pi_{\,k\,}(X)$ für $0\leq k\leq n$ trivial sind. "0-zusammenhängend" ist also ein Synonym für "wegzusammenhängend", und "1-zusammenhängend" bedeutet dasselbe wie "einfach zusammenhängend" im oben definierten Sinne.

Zusammenziehbar

→ Hauptartikel: Zusammenziehbarer Raum

Ein Raum X ist zusammenziehbar, falls er homotopieäquivalent zu einem Punkt ist, das heißt die Identität auf X homotop zu einer konstanten Abbildung ist. Zusammenziehbare Räume haben daher aus topologischer Sicht ähnliche Eigenschaften wie ein Punkt, insbesondere sind sie immer einfach zusammenhängend. Aber die Umkehrung gilt nicht: n-Sphären mit festem Radius sind nicht zusammenziehbar, obwohl sie für $n\ge 2$ einfach zusammenhängend sind.

Lokale Zusammenhangsbegriffe

Kamm: zusammenhängend aber nicht lokal zusammenhängend

Die folgenden Begriffe sind lokale Eigenschaften, sie machen also Aussagen über das Verhalten in Umgebungen von Punkten:

Lokal zusammenhängend

Ein Raum ist lokal zusammenhängend, falls es zu jeder Umgebung eines Punktes eine zusammenhängende kleinere Umgebung dieses Punktes gibt. Jeder Punkt besitzt dann eine Umgebungsbasis aus zusammenhängenden Mengen.

Ein lokal zusammenhängender Raum kann durchaus aus mehreren Zusammenhangskomponenten bestehen. Aber auch ein zusammenhängender Raum muss nicht unbedingt lokal zusammenhängend sein: Der „Kamm“, bestehend aus der Vereinigung der Intervalle $\{0\} \times [0,1]$ , $[0,1]\times \{0\}$ und $[0,1]\times \{1/n\}$ , ist zusammenhängend, doch jede genügend kleine Umgebung des Punktes (1,0) enthält unendlich viele nicht zusammenhängende Intervalle.

Buch: wegzusammenhängend, aber nicht lokal wegzusammenhängend

Lokal wegzusammenhängend

Ein Raum ist lokal wegzusammenhängend, falls jeder Punkt eine lokale Umgebungsbasis bestehend aus wegzusammenhängenden Mengen besitzt. Ein lokal wegzusammenhängender Raum ist wegzusammenhängend genau dann, wenn er zusammenhängend ist. Das oben gegebene Beispiel mit dem Graphen von sin(1/x) und der y-Achse ist daher nicht lokal wegzusammenhängend. Fügt man auch noch die x-Achse hinzu bekommt man einen zusammenhängenden, wegzusammenhängenden, aber nicht lokal wegzusammenhängenden Raum ("Warschauer Kreis"). Weiterhin ist das „Buch“ wegzusammenhängend, aber nicht lokal wegzusammenhängend für alle Punkte auf der Mittelsenkrechten mit Ausnahme des Schnittpunktes aller Geradenstücke.

Hawaiische Ohrringe: nicht semilokal einfach zusammenhängend und auch nicht lokal einfach zusammenhängend

Lokal einfach zusammenhängend

Ein Raum ist lokal einfach zusammenhängend, wenn jede Umgebung eines Punktes eine evtl. kleinere, einfach zusammenhängende Umgebung enthält.

Mannigfaltigkeiten sind lokal einfach zusammenhängend.

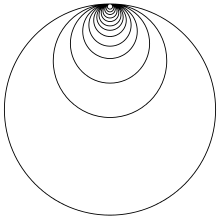
Ein Beispiel für einen nicht lokal einfach zusammenhängenden Raum sind die Hawaiischen Ohrringe: Die Vereinigung von Kreisen mit Radien 1/n als Teilmenge des $\mathbb R^2$ , so dass sich alle Kreise in einem Punkt berühren. Dann enthält jede Umgebung um den Berührpunkt einen geschlossenen Kreis, und ist daher nicht einfach zusammenhängend.

Semilokal einfach zusammenhängend

Ein Raum X ist semilokal einfach zusammenhängend, falls jeder Punkt eine Umgebung U besitzt, so dass sich jede Schleife in U in X zusammenziehen lässt (in U muss sie nicht notwendigerweise zusammenziehbar sein, daher nur semilokal).

Semilokal einfach zusammenhängend ist eine schwächere Bedingung als lokal einfach zusammenhängend: Ein Kegel über den Hawaiischen Ohrringen ist semilokal einfach zusammenhängend, da sich jede Schleife über die Kegelspitze zusammenziehen lässt. Er ist aber (aus dem gleichen Grund wie die Hawaiischen Ohrringe selbst) nicht lokal einfach zusammenhängend.

Basierend auf einem Artikel in:

Wikipedia.de