Homotopie

Eine Homotopie, die eine Kaffeetasse in einen Donut (einen Volltorus) überführt.

In der Topologie ist eine Homotopie (von griechisch ὁμός homos ‚gleich‘ und τόπος tópos ‚Ort‘, ‚Platz‘) eine stetige Deformation zwischen zwei Abbildungen von einem topologischen Raum in einen anderen, beispielsweise die Deformation einer Kurve in eine andere Kurve. Eine Anwendung von Homotopie ist die Definition der Homotopiegruppen, welche wichtige Invarianten in der algebraischen Topologie sind.

Der Begriff „Homotopie“ bezeichnet sowohl die Eigenschaft zweier Abbildungen, zueinander homotop (präferiert) zu sein, als auch die Abbildung („stetige Deformation“), die diese Eigenschaft vermittelt.

Definition

Eine Homotopie zwischen zwei stetigen Abbildungen $f,\,g\colon X\to Y$ ist eine stetige Abbildung

$H\colon X\times {[0,1]}\to Y$

mit der Eigenschaft

und

wobei [0,1] das Einheitsintervall ist. Der erste Parameter entspricht also dem der ursprünglichen Abbildungen und der zweite gibt den Grad der Deformation an. Besonders anschaulich wird die Definition, wenn man sich den zweiten Parameter als „Zeit“ vorstellt (vgl. Bild).

Man sagt, sei homotop zu und schreibt $f\sim g$ . Homotopie ist eine Äquivalenzrelation auf der Menge der stetigen Abbildungen $X\to Y$ , die zugehörigen Äquivalenzklassen heißen Homotopieklassen, die Menge dieser Klassen wird häufig mit [X,Y] bezeichnet.

Eine stetige Abbildung $f\colon X\to Y$ heißt nullhomotop, wenn sie homotop zu einer konstanten Abbildung ist.

Beispiel

Homotopie eines Kreises in R² auf einen Punkt

Sei $X=S^{1}\subset \mathbb {R} ^{2}$ der Einheitskreis in der Ebene und $Y=\mathbb {R} ^{2}$ die ganze Ebene. Die Abbildung sei die Einbettung von in , und sei die Abbildung, die ganz auf den Ursprung abbildet, also

$f(x)=x,\quad g(x)=0$ .

Dann sind und zueinander homotop. Denn

$H\colon X\times [0,1]\to \mathbb {R} ^{2}$ mit $H(x,t)=(1-t)\cdot f(x)$

ist stetig und erfüllt $H(x,0)=1\cdot f(x)$ und $H(x,1)=0\cdot f(x)=0=g(x)$ .

Relative Homotopie

Ist eine Teilmenge von , und stimmen zwei stetige Abbildungen $f,g\colon X\to Y$ auf überein, so heißen und homotop relativ zu , wenn es eine Homotopie $H\colon f\sim g$ gibt, für die H(e,t) für jedes $e\in E$ unabhängig von ist.

Homotopie zweier Kurven

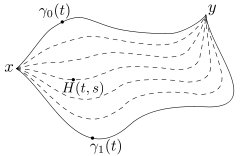
Ein wichtiger Spezialfall ist die Homotopie von Wegen relativ der Endpunkte: Ein Weg ist eine stetige Abbildung $\gamma \colon [0,1]\to X$ ; dabei ist [0,1] das Einheitsintervall. Zwei Wege heißen homotop relativ der Endpunkte, wenn sie homotop relativ $\{0,1\}$ sind, d.h. wenn die Homotopie die Anfangs- und Endpunkte festhält. (Sonst wären Wege in der gleichen Wegzusammenhangskomponente immer homotop.) Sind also $\gamma _{0}$ und $\gamma _{1}$ zwei Wege in mit $\gamma _{0}(0)=\gamma _{1}(0)=x$ und $\gamma _{0}(1)=\gamma _{1}(1)=y$ , so ist eine Homotopie relativ der Endpunkte zwischen ihnen eine stetige Abbildung

$H:[0,1]\times [0,1]\to Y$

mit $H(t,0)=\gamma _{0}(t)$ , $H(t,1)=\gamma _{1}(t)$ , H(0,s)=x und H(1,s)=y .

Ein Weg heißt nullhomotop genau dann, wenn er homotop zum konstanten Weg $\gamma (t)=x_{0}$ ist.

Der andere häufig auftretende Fall ist die Homotopie von Abbildungen zwischen punktierten Räumen. Sind $(X,x_{0})$ und $(Y,y_{0})$ punktierte Räume, so sind zwei stetige Abbildungen $f,g\colon (X,x_{0})\to (Y,y_{0})$ homotop als Abbildungen von punktierten Räumen, wenn sie relativ $x_{0}$ homotop sind.

Beispiel: Die Fundamentalgruppe

Die Menge der Homotopieklassen von Abbildungen punktierter Räume von $(S^{1},*)$ nach $(X,x_{0})$ ist die Fundamentalgruppe von zum Basispunkt $x_{0}$ .

Ist zum Beispiel $(X,x_{0})$ ein Kreis mit einem beliebigen ausgewählten Punkt $x_{0}$ , dann ist der Weg, der durch einmaliges Umrunden des Kreises beschrieben wird, nicht homotop zum Weg, den man durch Stillstehen am Ausgangspunkt $x_{0}$ erhält.

Homotopieäquivalenz

→ Hauptartikel: Homotopieäquivalenz

Seien und zwei topologische Räume und sind $f\colon X\to Y$ und $g\colon Y\to X$ stetige Abbildungen. Dann sind die Verknüpfungen $g\circ f$ und $f\circ g$ jeweils stetige Abbildungen von bzw. auf sich selbst, und man kann versuchen, diese zur Identität auf X bzw. Y zu homotopieren.

Falls es solche und gibt, dass $g\circ f$ homotop zu $id_{X}$ und $f\circ g$ homotop zu $id_{Y}$ ist, so nennt man und homotopieäquivalent oder vom gleichen Homotopietyp. Die Abbildungen und heißen dann Homotopieäquivalenzen.

Homotopieäquivalente Räume haben die meisten topologischen Eigenschaften gemeinsam. Falls und homotopieäquivalent sind, so gilt

falls wegzusammenhängend, so auch .
falls und wegzusammenhängend, so sind die Fundamentalgruppen und die höheren Homotopiegruppen isomorph.
die Homologie- und Kohomologiegruppen von und sind gleich.
und sind Deformationsretrakte eines topologischen Raums .

Isotopie

Definition

Wenn zwei gegebene homotope Abbildungen $f\colon X\to Y$ und $g\colon X\to Y$ zu einer bestimmten Regularitätsklasse gehören oder andere zusätzliche Eigenschaften besitzen, kann man sich fragen, ob die beiden innerhalb dieser Klasse durch einen Weg miteinander verbunden werden können. Dies führt zum Konzept der Isotopie. Eine Isotopie ist eine Homotopie

$H\colon X\times [0,1]\to Y$

wie oben, wobei alle Zwischenabbildungen $H_{t}:=H(\cdot ,t)$ (für festes t) ebenfalls die geforderten Zusatzeigenschaften besitzen sollen. Die zugehörigen Äquivalenzklassen heißen Isotopieklassen.

Beispiele

Zwei Homöomorphismen sind also isotop, wenn eine Homotopie existiert, so dass alle $H_{t}$ Homöomorphismen sind. Zwei Diffeomorphismen sind isotop, wenn alle $H_{t}$ selbst Diffeomorphismen sind. (Man bezeichnet sie dann auch als diffeotop.) Zwei Einbettungen sind isotop, wenn alle $H_{t}$ Einbettungen sind.

Unterschied zur Homotopie

Zu verlangen, dass zwei Abbildungen isotop sind, kann tatsächlich eine stärkere Anforderung sein, als zu verlangen, dass sie homotop sind. Zum Beispiel ist der Homöomorphismus der Einheitskreisscheibe in $\mathbb {R} ^{2}$ , der durch f(x,y)=(-x,-y) definiert ist, dasselbe wie eine 180-Grad-Drehung um den Nullpunkt, darum sind die Identitätsabbildung und isotop, denn sie können durch Drehungen miteinander verbunden werden. Im Gegensatz dazu ist die Abbildung auf dem Intervall $\left[-1,1\right]$ in $\mathbb {R}$ , definiert durch f(x)=-x nicht isotop zur Identität. Das liegt daran, dass jede Homotopie der beiden Abbildungen zu einem bestimmten Zeitpunkt die beiden Endpunkte miteinander vertauschen muss; zu diesem Zeitpunkt werden sie auf denselben Punkt abgebildet und die entsprechende Abbildung ist kein Homöomorphismus. Hingegen ist homotop zur Identität, zum Beispiel durch die Homotopie $H''\colon \left[-1,1\right]\times \left[0,1\right]\to \left[-1,1\right]$ , gegeben durch $H(x,t)=2tx-x$ .

Anwendungen

In der Geometrischen Topologie werden Isotopien benutzt, um Äquivalenzrelationen herzustellen.

Zum Beispiel in der Knotentheorie – wann sind zwei Knoten $K_{1}$ und $K_{2}$ als gleich zu betrachten? Die intuitive Idee, den einen Knoten in den anderen zu deformieren, führt dazu, dass man einen Weg von Homöomorphismen verlangt: Eine Isotopie, die mit der Identität des dreidimensionalen Raumes beginnt und bei einem Homöomorphismus h endet, so dass h den Knoten $K_{1}$ in den Knoten $K_{2}$ überführt. Eine solche Isotopie des umgebenden Raumes wird ambiente Isotopie oder Umgebungsisotopie genannt.

Eine andere wichtige Anwendung ist die Definition der Abbildungsklassengruppe Mod(M) einer Mannigfaltigkeit M. Man betrachtet Diffeomorphismen von M „bis auf Isotopie“, das heißt, dass Mod(M) die (diskrete) Gruppe der Diffeomorphismen von M ist, modulo der Gruppe der Diffeomorphismen, die isotop zur Identität sind.

Homotopie kann in der numerischen Mathematik für eine robuste Initialisierung zur Lösung von differential-algebraischen Gleichungen eingesetzt werden (siehe Homotopieverfahren).

Kettenhomotopie

Zwei Kettenhomomorphismen

$f_{\bullet },g_{\bullet }\colon (A_{\bullet },d_{A,\bullet })\to (B_{\bullet },d_{B,\bullet })$

zwischen Kettenkomplexen $(A_{\bullet },d_{A,\bullet })$ und $(B_{\bullet },d_{B,\bullet })$ heißen kettenhomotop, wenn es einen Homomorphismus

$K_{\bullet }\colon (A_{\bullet })\to (B_{\bullet +1})$

mit

$d_{B,{\bullet +1}}K_{\bullet }+K_{\bullet -1}d_{A,{\bullet }}=f_{\bullet }-g_{\bullet }$

gibt.

Wenn $f,g\colon X\to Y$ homotope Abbildungen zwischen topologischen Räumen sind, dann sind die induzierten Abbildungen der singulären Kettenkomplexe

$f_{\bullet },g_{\bullet }\colon (C_{\bullet }(X),d_{\bullet })\to (C_{\bullet }(Y),d_{\bullet })$

kettenhomotop.

Punktierte Homotopie

→ Hauptartikel: Punktierter topologischer Raum

Zwei punktierte Abbildungen

$f,g\colon (X,x_{0})\to (Y,y_{0})$

heißen homotop, wenn es eine stetige Abbildung $H\colon X\times \left[0,1\right]\to Y$ mit

und

für alle $x\in X$

$H(x_{0},t)=y_{0}$ für alle $t\in \left[0,1\right]$

gibt. Die Menge der Homotopieklassen punktierter Abbildungen wird mit $\left[X,Y\right]$ bezeichnet.

Basierend auf einem Artikel in:

Wikipedia.de