Messbare Funktion
Messbare Funktionen werden in der Maßtheorie untersucht, einem Teilbereich der Mathematik, der sich mit der Verallgemeinerung von Längen- und Volumenbegriffen beschäftigt. Von messbaren Funktionen wird verlangt, dass das Urbild gewisser Mengen wieder in einem bestimmten Mengensystem liegt. Messbare Funktionen spielen eine wichtige Rolle in der Stochastik und der Maßtheorie, da durch sie Zufallsvariablen und Bildmaße konstruiert werden können.
Definition
Gegeben seien zwei Messräume
und
,
das heißt je eine Grundmenge und eine σ-Algebra
auf dieser Menge, sowie eine Funktion
.
Die Funktion
heißt nun eine messbare Funktion, wenn das Urbild jeder Menge
unter
Element aus
ist.[1]
Formalisiert lautet diese Bedingung
, für alle
.
Eine solche Funktion wird auch als -
-messbar
bezeichnet. Eine Funktion heißt Borel-messbar (Lebesgue-messbar),
wenn sie bezüglich zweier Borelscher
σ-Algebren (Lebesguescher σ-Algebren) messbar ist. Teilweise werden auch
Mischformen (Lebesgue-Borel-messbar oder Borel-Lebesgue-messbar)
verwendet. Zu beachten ist, dass kein Maß
definiert sein muss, um eine messbare Funktion zu definieren.
Elementare Beispiele
- Sind zwei Messräume
und
gegeben, und ist
die triviale σ-Algebra, so ist jede Funktion
-
-messbar, unabhängig von der Wahl der Funktion und der σ-Algebra
. Dies liegt daran, dass immer
und
gilt. Diese Mengen sind aber immer in der σ-Algebra
enthalten. Wählt man hingegen als σ-Algebra die Potenzmenge
, so ist ebenfalls jede Funktion
-
-messbar, unabhängig von der Wahl der Funktion und der σ-Algebra
. Dies liegt daran, dass jedes Urbild
immer in der Potenzmenge liegt, da diese per Definition jede Teilmenge der Obermenge enthält.
- Jede konstante Funktion, also jede Funktion der Form
für alle
, ist messbar. Ist nämlich
, so ist
-
- Da die Grundmenge und die leere Menge in jeder beliebigen σ-Algebra
enthalten sind, sind sie insbesondere in
enthalten und die Funktion ist messbar.
- Sind
und
Messräume, dann ist für beliebiges
die Indikatorfunktion
eine
-
-messbare Funktion. Es gilt dann
und
sowie
und
. Diese Mengen sind aber nach Voraussetzung in der σ-Algebra enthalten.
Einordnung
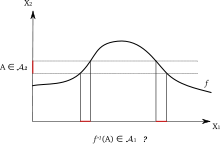
Der Begriff der Messbarkeit wird durch die Definition der Integration von Henri
Lebesgue motiviert: Für die Lebesgue-Integration
einer Funktion
bezüglich des Lebesgue-Maßes
muss Mengen der Form
ein Maß zugeordnet sein. Beispiele für Funktionen, für die dies nicht möglich
ist, sind Indikatorfunktionen
von Vitali-Mengen.
Die Definition der Lebesgue-Integration für beliebige Maßräume führt dann zu
obiger Definition der messbaren Funktion.
Der Begriff der messbaren Funktion hat Parallelen zur Definition der stetigen Funktion.
Eine Funktion zwischen topologischen
Räumen
und
ist genau dann stetig, wenn die Urbilder offener Mengen von
wiederum offene Mengen von
sind. Die von den offenen Mengen erzeugte
σ-Algebra ist die borelsche
σ-Algebra. Eine stetige Funktion ist also messbar bezüglich der
Borel-σ-Algebren von
und
kurz borel-messbar. Eine gewisse Umkehrung dieser Aussage ist der Satz
von Lusin.
Messbare Funktionen spielen als Zufallsvariablen eine wichtige Rolle in der Wahrscheinlichkeitstheorie.
Eigenschaften
Messbare Funktionen und Erzeugendensysteme
Oftmals ist eine σ-Algebra viel zu groß, um jede Menge aus ihr direkt angeben
zu können oder das Urbild jeder Menge zu überprüfen. Die Überprüfung einer
Funktion auf Messbarkeit wird aber dadurch erleichtert, dass man dies nur auf
den Urbildern eines Erzeugers machen muss. Ist also
ein Erzeuger von
,
sprich ist
,
so ist die Funktion
genau dann messbar, wenn
für alle
gilt.
Daraus folgt direkt, dass stetige Funktionen zwischen topologischen Räumen, die mit der borelschen σ-Algebra versehen sind, immer messbar sind, da Urbilder offener Mengen immer offen sind. Da die borelsche σ-Algebra aber von den offenen Mengen erzeugt wird und demnach die Urbilder des Erzeugers wieder im Erzeuger liegen, folgt die Messbarkeit.
Initial-σ-Algebra
Zu jeder Abbildung ,
wobei
mit der σ-Algebra
versehen ist, lässt sich eine kleinste σ-Algebra angeben, bezüglich derer die
Funktion
messbar ist. Diese σ-Algebra nennt man dann die Initial-σ-Algebra
der Funktion und bezeichnet sie mit
oder mit
.
Sie lässt sich auch für beliebige Familien von Funktionen
definieren. Sie ist dann die kleinste σ-Algebra, bezüglich derer alle
messbar sind, und wird dann mit
oder
bezeichnet. Für eine einzelne Funktion
ist aufgrund der Operationsstabilität des Urbildes bereits
die Initial-σ-Algebra.
Verkettungen messbarer Funktionen
Sind ,
und
Messräume und ist
-
-messbar
und
-
-messbar,
so ist die Funktion
-
-messbar.
Unter Umständen kann auch aus der Messbarkeit von verknüpften Funktionen auf
die Messbarkeit ihrer Teilfunktionen geschlossen werden: Sind
Funktionen von
nach
und ist
die Initial-σ-Algebra, dann ist eine Funktion
von
nach
genau dann messbar, wenn
für alle
-
-messbar
ist.
Faktorisierungslemma
Das Faktorisierungslemma ist ein maßtheoretischer Hilfssatz über die Messbarkeit von Funktionen, der bei einigen weitreichenden stochastischen Konstruktionen und Sätzen der mathematischen Statistik verwendet wird. Das Lemma wird beispielsweise bei der Konstruktion der faktorisierten bedingten Erwartung eingesetzt, die ein Schritt auf dem Weg zur regulären bedingten Verteilung ist. Das Lemma besagt: Wenn eine Abbildung
gegeben ist, dann ist die Abbildung
genau dann -messbar,
wenn eine Funktion
existiert, so dass
messbar ist und
gilt. Dabei ist
eine σ-Algebra auf
und
die von
erzeugte σ-Algebra.
Messbarkeit reellwertiger Funktionen
Überprüfung
Für eine Abbildung
von einem Messraum
nach
gilt, dass
genau dann messbar ist, wenn eines der Mengensysteme
,
,
,
in
liegt. Dabei ist
etc. als Abkürzung für
zu verstehen. Es würde auch ausreichen, wenn
nur alle rationalen Zahlen durchliefe, denn die angegebenen Intervalle bilden
immer ein Erzeugendensystem der borelschen σ-Algebra.
Messbare Funktionen
Die folgenden Funktionen
sind beispielsweise messbar:
Ist außerdem eine Funktion
gegeben, so ist sie genau dann messbar, wenn jede ihrer Komponentenfunktionen
-
-messbar
ist.
Sind
messbare Funktionen von
nach
,
so sind auch
und
messbar. Ist
messbar von
nach
,
so ist
messbar. Vereinbart man die Konvention
,
so ist sogar
messbar.
Ist eine Funktionenfolge -
-messbarer
Funktionen
gegeben, so sind auch das Infimum, das Supremum sowie der Limes inferior und der
Limes superior dieser Folge wieder messbar.
Approximation
Jede positive messbare Funktion lässt sich durch eine monoton wachsende Funktionenfolge von einfachen Funktionen (also Linearkombinationen von Indikatorfunktionen von messbaren Mengen) approximieren. Eine Funktionenfolge, die das leistet, ist beispielsweise
.
Diese Approximationseigenschaft wird bei der Konstruktion des Lebesgue-Integrals genutzt, welches zuerst nur für einfache Funktionen definiert wird und dann auf alle messbaren Funktionen fortgesetzt wird.
Lebesgue- und Borelmessbare Funktionen
Eine (reelle) Lebesgue-Borel-messbare Funktion ist nicht unbedingt Borel-Borel-messbar. Auch ist eine Lebesgue-Borel-messbare Funktion nicht unbedingt Lebesgue-Lebesgue-messbar. Die Verkettung zweier Lebesgue-Borel-messbarer Funktionen ist also nicht zwangsläufig wiederum Lebesgue-Borel-messbar.
Verwandte Begriffe
Starke Messbarkeit
Ist eine Funktion in einem metrischen Raum punktweiser Limes von Elementarfunktionen, d. h. messbaren Funktionen mit endlichem Bild, so heißt sie „stark messbar“.
- Jede messbare Funktion mit separablem Bild ist stark messbar.
- Jede stark messbare Funktion ist messbar.
Starke Messbarkeit und Messbarkeit unterscheiden sich nur voneinander, wenn der Zielraum nicht-separabel ist. Dies ist beispielsweise bei der Definition von verallgemeinerten Integralen wie dem Bochner-Integral der Fall.
Bimessbare Funktionen
Messbare Funktionen, deren Umkehrabbildung ebenfalls messbar ist, werden bimessbare Funktionen genannt.
Abgrenzung
Eine Teilmenge eines Messraums heißt messbar, wenn sie Element der σ-Algebra des Messraums ist und ihr somit potentiell ein Maß zugeordnet werden kann. Des Weiteren existiert noch die Messbarkeit nach Carathéodory von Mengen bezüglich eines äußeren Maßes. Hier wird nur ein äußeres Maß benötigt.
Literatur
- Jürgen Elstrodt: Maß- und Integrationstheorie. 6., korrigierte Auflage. Springer-Verlag, Berlin Heidelberg 2009, ISBN 978-3-540-89727-9.
- Achim Klenke: Wahrscheinlichkeitstheorie. 3. Auflage. Springer-Verlag, Berlin Heidelberg 2013, ISBN 978-3-642-36017-6.
- Henri Lebesgue: Leçons sur l'intégration et la recherche des fonctions primitives. Gauthier-Villars, Paris 1904.
Anmerkung
- ↑
und
sind jeweils messbare Mengen bezogen auf
und
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.04. 2023