
Maß (Mathematik)

Ein Maß ist in der Mathematik eine Funktion, die geeigneten Teilmengen einer Grundmenge Zahlen zuordnet, die als „Maß“ für die Größe dieser Mengen interpretiert werden können. Dabei müssen sowohl der Definitionsbereich eines Maßes, also die messbaren Mengen, als auch die Zuordnung selbst gewisse Voraussetzungen erfüllen, wie sie beispielsweise durch elementargeometrische Begriffe der Länge einer Strecke, dem Flächeninhalt einer geometrischen Figur oder dem Volumen eines Körpers nahegelegt werden.
Das Teilgebiet der Mathematik, das sich mit der Konstruktion und der Untersuchung von Maßen beschäftigt, ist die Maßtheorie. Der allgemeine Maßbegriff geht zurück auf Arbeiten von Émile Borel, Henri Léon Lebesgue, Johann Radon und Maurice René Fréchet. Dabei stehen Maße stets in engem Zusammenhang mit der Integration von Funktionen und bilden die Grundlage moderner Integralbegriffe (siehe Lebesgue-Integral). Seit der Axiomatisierung der Wahrscheinlichkeitsrechnung durch Andrei Kolmogorow ist die Stochastik ein weiteres großes Anwendungsgebiet für Maße. Dort werden Wahrscheinlichkeitsmaße verwendet, um zufälligen Ereignissen, die als Teilmengen eines Ergebnisraums aufgefasst werden, Wahrscheinlichkeiten zuzuordnen.
Einführung und Geschichte
Der elementargeometrische Flächeninhalt ordnet ebenen geometrischen
Figuren wie Rechtecken, Dreiecken oder Kreisen, also gewissen Teilmengen der
euklidischen
Ebene, Zahlenwerte zu. Flächeninhalte können gleich null sein,
beispielsweise bei der leeren
Menge, aber auch bei einzelnen Punkten oder bei Strecken. Auch der „Wert“
(unendlich) kommt
z.B. bei Halbebenen
oder dem Äußeren von Kreisen als Flächeninhalt vor. Allerdings dürfen keine
negativen Zahlen als Flächeninhalte auftreten.

Weiterhin besitzt der Flächeninhalt ebener geometrischer Figuren eine Eigenschaft, die Additivität genannt wird: Zerlegt man eine Figur in zwei oder mehr Teile, beispielsweise ein Rechteck mittels einer Diagonale in zwei Dreiecke, dann ist der Flächeninhalt der Ausgangsfigur die Summe der Flächeninhalte der Teile. „Zerlegen“ bedeutet hier, dass die Teile paarweise disjunkt sein müssen (je zwei Teile haben also keine gemeinsamen Punkte) und dass die Vereinigung aller Teile die Ausgangsfigur ergibt. Für die Messung von Flächeninhalten komplizierterer Figuren, wie Kreisflächen oder Flächen, die zwischen Funktionsgraphen eingeschlossen sind (also für die Berechnung von Integralen), müssen Grenzwerte von Flächeninhalten betrachtet werden. Dazu ist es wichtig, dass die Additivität auch dann noch gilt, wenn Flächen in eine Folge von paarweise disjunkten Teilflächen zerlegt werden. Diese Eigenschaft wird abzählbare Additivität oder σ-Additivität genannt.

Die Bedeutung der σ-Additivität für den Maßbegriff wurde erstmals von Émile Borel erkannt, der 1894 bewies, dass die elementargeometrische Länge diese Eigenschaft besitzt. Das eigentliche Maßproblem formulierte und untersuchte Henri Lebesgue im Jahre 1902 in seiner Doktorarbeit: Er konstruierte ein σ-additives Maß für Teilmengen der reellen Zahlen (das Lebesgue-Maß), das die Länge von Intervallen fortsetzt, allerdings nicht für alle Teilmengen, sondern für ein System von Teilmengen, die er messbare Mengen nannte. Im Jahre 1905 zeigte Giuseppe Vitali, dass eine konsistente Erweiterung des Längenbegriffs auf alle Teilmengen der reellen Zahlen unmöglich ist, also dass das Maßproblem nicht lösbar ist.
Da wichtige Maße, wie eben das Lebesgue-Maß, nicht für alle Teilmengen (also auf der Potenzmenge) der Grundmenge definiert werden können, müssen geeignete Definitionsbereiche für Maße betrachtet werden. Die σ-Additivität legt es nahe, dass Systeme messbarer Mengen abgeschlossen gegenüber abzählbaren Mengenoperationen sein sollten. Das führt auf die Forderung, dass die messbaren Mengen eine σ-Algebra bilden müssen. Das heißt: Die Grundmenge selbst ist messbar und Komplemente sowie abzählbare Vereinigungen messbarer Mengen sind wiederum messbar.
In der Folgezeit erweiterten Thomas Jean Stieltjes und Johann Radon die Konstruktion des Lebesgue-Maßes auf
allgemeinere Maße im -dimensionalen
Raum, die Lebesgue-Stieltjes-Maße.
Maurice René Fréchet betrachtete ab 1915 auch Maße und Integrale auf beliebigen
abstrakten Mengen. Im Jahre 1933 veröffentlichte
Andrei Kolmogorow sein Lehrbuch
Grundbegriffe der Wahrscheinlichkeitsrechnung, in dem er Maßtheorie
verwendet, um eine strenge axiomatische Begründung der
Wahrscheinlichkeitstheorie
zu geben.
Definition
Es sei
eine σ-Algebra über einer
nicht-leeren Grundmenge
.
Eine Funktion
heißt Maß auf
,
wenn die beiden folgenden Bedingungen erfüllt sind:
- σ-Additivität: Für jede Folge
paarweise disjunkter Mengen aus
gilt
.
Ist die σ-Algebra aus dem Zusammenhang klar, so spricht man auch von einem
Maß auf .
Eine Teilmenge von ,
die in
liegt, wird messbar genannt. Für solch ein
heißt
das Maß der Menge
.
Das Tripel
wird Maßraum genannt. Das
Paar
bestehend aus der Grundmenge und der darauf definierten σ-Algebra heißt Messraum
oder auch messbarer Raum. Ein Maß
ist also eine auf einem Messraum definierte nicht-negative σ-additive
Mengenfunktion mit
.
Das Maß
heißt Wahrscheinlichkeitsmaß (oder normiertes Maß), wenn zusätzlich
gilt. Ein Maßraum
mit einem Wahrscheinlichkeitsmaß
ist ein Wahrscheinlichkeitsraum. Ist allgemeiner
,
so nennt man
ein endliches
Maß. Existieren abzählbar viele Mengen, deren Maß endlich ist und deren
Vereinigung ganz
ergibt, dann wird
ein σ-endliches
(oder σ-finites) Maß genannt.
Anmerkungen und erste Beispiele
- Ein Maß nimmt also nicht-negative Werte aus den erweiterten
reellen Zahlen
an. Für das Rechnen mit
gelten die üblichen Konventionen, zusätzlich ist es nützlich
zu setzen.
- Da alle Summanden der Reihe
nicht-negativ sind, ist diese entweder konvergent oder divergiert gegen
.
- Die Forderung, dass die leere Menge das Maß null besitzt, schließt den
uninteressanten Fall
für alle
aus. In der Tat lässt sich die Forderung
äquivalent ersetzen durch die Bedingung, dass ein
existiert mit
. Dagegen sind die trivialen Fälle
für alle
(das sogenannte Nullmaß) sowie
für alle
(und
) Maße im Sinne der Definition.
- Für ein Element
wird durch
-
- für
ein Maß definiert. Es wird Diracmaß an der Stelle
genannt und ist ein Wahrscheinlichkeitsmaß.
- Die Abbildung
, die jeder endlichen Menge
die Anzahl ihrer Elemente, also ihre Mächtigkeit
, sowie den unendlichen Mengen in
den Wert
zuweist, heißt Zählmaß. Das Zählmaß ist ein endliches Maß, wenn
eine endliche Menge ist, und ein σ-endliches Maß, wenn
höchstens abzählbar ist.
- Das
-dimensionale Lebesgue-Maß
ist ein Maß auf der σ-Algebra der Lebesgue-messbaren Teilmengen von
. Es ist eindeutig bestimmt durch die Forderung, dass es den
-dimensionalen Hyperrechtecken ihr Volumen zuordnet:
-
.
- Das Lebesgue-Maß ist nicht endlich, aber σ-endlich.
- Das Hausdorff-Maß ist eine Verallgemeinerung des Lebesgue-Maßes auf nicht notwendig ganzzahlige Dimensionen. Mit seiner Hilfe lässt sich die Hausdorff-Dimension definieren, ein Dimensionsbegriff, mit dem beispielsweise fraktale Mengen untersucht werden können.
Eigenschaften
Rechenregeln
Direkt aus der Definition ergeben sich die folgenden elementaren Rechenregeln
für ein Maß :
- endliche Additivität: Für paarweise disjunkte Mengen
gilt
.
- Subtraktivität: Für
mit
und
gilt
.
- Monotonie: Für
mit
gilt
.
- Für
gilt stets
. Mit dem Prinzip von Inklusion und Exklusion lässt sich diese Formel im Falle endlicher Maße auf Vereinigungen und Schnitte endlich vieler Mengen verallgemeinern.
- σ-Subadditivität:
Für eine beliebige Folge
von Mengen aus
gilt
.
Stetigkeitseigenschaften
Die folgenden Stetigkeitseigenschaften sind grundlegend für die Approximation messbarer Mengen. Sie folgen direkt aus der σ-Additivität.
- σ-Stetigkeit
von unten: Ist
eine aufsteigende Folge von Mengen aus
und
, dann gilt
.
- σ-Stetigkeit
von oben: Ist
eine absteigende Folge von Mengen aus
mit
und
, dann gilt
.
Eindeutigkeitssatz
Für zwei Maße
auf einem gemeinsamen Messraum
gilt der folgende Eindeutigkeitssatz:
Es gebe einen durchschnittsstabilen
Erzeuger
von
,
d.h. es gilt
und für alle
ist
,
mit folgenden Eigenschaften:
- Für alle
gilt
, also
, und
- Es gibt eine Folge
von Mengen in
mit
und
für alle
.
Dann gilt .
Für endliche Maße mit
ist die Bedingung 2 automatisch erfüllt. Insbesondere sind zwei
Wahrscheinlichkeitsmaße gleich, wenn sie auf einem durchschnittsstabilen
Erzeuger der Ereignisalgebra übereinstimmen.
Der Eindeutigkeitssatz liefert zum Beispiel die Eindeutigkeit der Fortsetzung eines Prämaßes zu einem Maß mittels eines äußeren Maßes und dem Maßerweiterungssatz von Carathéodory.
Linearkombinationen von Maßen
Für eine Familie
von Maßen auf dem gleichen Messraum und für nicht-negative reelle Konstanten
wird durch
wieder ein Maß definiert. Insbesondere sind Summen und nicht-negative Vielfache
von Maßen ebenfalls Maße.
Ist beispielsweise
eine abzählbare Grundmenge und
,
dann ist
mit den Diracmaßen
ein Maß auf der Potenzmenge von
.
Umgekehrt kann man zeigen, dass man auf diese Weise bei abzählbarer Grundmenge
alle Maße auf der Potenzmenge erhält.
Sind
Wahrscheinlichkeitsmaße auf
und
nicht-negative reelle Zahlen mit
,
dann ist die Konvexkombination
wieder ein Wahrscheinlichkeitsmaß. Durch Konvexkombination von Diracmaßen erhält
man diskrete
Wahrscheinlichkeitsverteilungen, allgemein ergeben sich Mischverteilungen.
Konstruktion von Maßen
Maßerweiterungssatz

Da die Elemente von σ-Algebren, wie beispielsweise bei der borelschen
σ-Algebra auf ,
oft nicht explizit angegeben werden können, werden Maße häufig durch Fortsetzung von
Mengenfunktionen konstruiert. Das wichtigste Hilfsmittel hierzu ist der
Maßerweiterungssatz
von Carathéodory. Er besagt, dass sich jede nicht-negative σ-additive
Mengenfunktion auf einem Mengenring
(ein sog. Prämaß)
zu einem Maß auf der von
erzeugten σ-Algebra fortsetzen lässt.
Die Fortsetzung ist eindeutig, wenn das Prämaß σ-endlich ist.
Beispielsweise bilden alle Teilmengen von ,
die sich als endliche Vereinigung von achsenparallelen
-dimensionalen
Intervallen darstellen lassen, einen Mengenring. Der elementare Volumeninhalt
dieser sogenannten Figuren, der Jordan-Inhalt, ist ein
Prämaß auf diesem Mengenring. Die von den Figuren erzeugte σ-Algebra ist die
borelsche σ-Algebra und die Fortsetzung des Jordan-Inhalts nach Carathéodory
ergibt das Lebesgue-Borel-Maß.
Nullmengen, Vervollständigung von Maßen
Ist
ein Maß und
eine Menge mit
,
dann heißt
Nullmenge. Es ist naheliegend, Teilmengen einer Nullmenge ebenfalls das Maß null
zuzuordnen. Allerdings müssen solche Mengen nicht unbedingt messbar sein, also
wieder in
liegen. Ein Maßraum, in dem Teilmengen von Nullmengen stets messbar sind, wird
vollständig genannt. Zu einem Maßraum, der nicht vollständig ist, lässt sich ein
vollständiger Maßraum – genannt die Vervollständigung – konstruieren. Zum
Beispiel ist die Vervollständigung des Lebesgue-Borel-Maßes das Lebesgue-Maß auf
den Lebesgue-messbaren Teilmengen des
.
Maße auf den reellen Zahlen
Das Lebesgue-Maß
auf
ist dadurch charakterisiert, dass es Intervallen
ihre Länge
zuweist. Dessen Konstruktion kann mit Hilfe einer monoton
wachsenden Funktion
verallgemeinert werden zu den Lebesgue-Stieltjes-Maßen
,
die den Intervallen
die „gewichtete Länge“
zuordnen. Wenn die Funktion
zusätzlich rechtsseitig
stetig ist, dann wird hierdurch ein Prämaß auf dem Mengenring der endlichen
Vereinigungen solcher Intervalle definiert. Dieses kann nach Carathéodory zu
einem Maß auf den Borelmengen von
bzw. zu dessen Vervollständigung erweitert werden. Beispielsweise ergibt sich
für die identische Abbildung
wieder das Lebesgue-Maß; ist dagegen
eine stückweise konstante Treppenfunktion, so erhält man Linearkombinationen von
Diracmaßen.
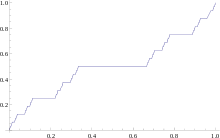
Falls eine rechtsseitig stetige und monoton wachsende Funktion
zusätzlich noch die Bedingungen
und
erfüllt, ist das auf diese Weise konstruierte Lebesgue-Stieltjes-Maß
ein Wahrscheinlichkeitsmaß. Dessen Verteilungsfunktion
ist gleich
,
das bedeutet
.
Umgekehrt besitzt jede Verteilungsfunktion
eines Wahrscheinlichkeitsmaßes auf
die obigen Eigenschaften. Mit Hilfe von Verteilungsfunktionen lassen sich daher
auch solche Wahrscheinlichkeitsmaße auf
einfach darstellen, die weder diskret sind noch eine Lebesgue-Dichte besitzen,
wie zum Beispiel die Cantor-Verteilung.
Einschränkung von Maßen
Wie jede Funktion lässt sich ein Maß
natürlich auf einen kleineren Definitionsbereich, also auf eine σ-Algebra
einschränken.
Beispielsweise erhält man durch Einschränkung des Lebesgue-Maßes auf die
borelsche σ-Algebra wieder das Lebesgue-Borel-Maß zurück.
Interessanter ist eine Einschränkung auf eine kleinere Grundmenge :
Ist
ein Maßraum und
,
dann wird durch
eine σ-Algebra auf
definiert, die sogenannte Spur-σ-Algebra.
Es gilt
genau dann, wenn
und
ist. Für diese
wird durch
ein Maß auf
definiert, das Einschränkung (oder Spur) von
auf
genannt wird. Zum Beispiel erhält man durch Einschränkung des Lebesgue-Maßes
von
auf das Intervall
wegen
ein Wahrscheinlichkeitsmaß auf
,
die stetige
Gleichverteilung.
Bildmaß
Maße lassen sich mit Hilfe von messbaren
Funktionen von einem Maßraum auf einen weiteren Messraum transformieren.
Sind
und
Messräume, dann heißt eine Funktion
messbar, wenn für alle
das Urbild
in
liegt. Ist nun
ein Maß auf
,
dann ist die Funktion
mit
für
ein Maß auf
.
Es heißt Bildmaß von
unter
und wird häufig mit
oder
bezeichnet.
Das Verhalten von Integralen bei der Transformation von Maßen wird durch den Transformationssatz beschrieben. Durch Bildmaße ist es in der Analysis möglich, Maße auf Mannigfaltigkeiten zu konstruieren.
Bildmaße von Wahrscheinlichkeitsmaßen sind wieder Wahrscheinlichkeitsmaße. Diese Tatsache spielt bei der Betrachtung von Wahrscheinlichkeitsverteilungen von Zufallsvariablen in der Stochastik eine wichtige Rolle.
Maße mit Dichten
Maße werden oft als „unbestimmte Integrale“ von Funktionen bezüglich anderer
Maße konstruiert. Ist
ein Maßraum und
eine nicht-negative messbare Funktion, dann wird durch
für
ein weiteres Maß auf
definiert. Die Funktion
wird Dichtefunktion
von
bezüglich
(kurz eine
-Dichte)
genannt. Eine übliche Schreibweise ist
.
Der Satz
von Radon-Nikodým gibt Auskunft darüber, welche Maße mit Hilfe von Dichten
dargestellt werden können: Ist
σ-endlich, so ist dies genau dann möglich, wenn alle Nullmengen von
auch Nullmengen von
sind.
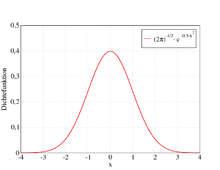
In der Stochastik werden die Verteilungen stetiger Zufallsvariabler, wie beispielsweise die Normalverteilung, häufig durch Dichten bezüglich des Lebesgue-Maßes angegeben.
Produktmaße
Lässt sich eine Grundmenge als kartesisches
Produkt schreiben und sind auf den einzelnen Faktoren Maße gegeben, so kann
auf ihr ein sogenanntes Produktmaß konstruiert werden. Für zwei Maßräume
und
bezeichne
die Produkt-σ-Algebra.
Das ist die kleinste σ-Algebra auf
,
die alle Mengenprodukte
mit
und
enthält. Falls
und
σ-endlich sind, dann existiert genau ein Maß
auf
mit
,
das Produktmaß genannt und mit
bezeichnet wird. Völlig analog lassen sich auch Produkte endlich vieler Maße
bilden. Beispielsweise erhält man so das Lebesgue-Borel-Maß auf dem
-dimensionalen
euklidischen Raum
als
-faches
Produkt aus dem Lebesgue-Borel-Maß auf den reellen Zahlen.
Mit Hilfe des Satzes
von Fubini lassen sich Integrale bezüglich eines Produktmaßes
meist berechnen, indem man schrittweise Integrationen bezüglich der einzelnen
Maße
ausführt. Auf diese Weise können beispielsweise Flächen- und Volumenberechnungen
auf die Bestimmung eindimensionaler Integrale zurückgeführt werden.
Im Gegensatz zu allgemeinen Maßen können unter bestimmten Voraussetzungen bei Wahrscheinlichkeitsmaßen beliebige (sogar überabzählbare) Produkte gebildet werden. Produkte von Wahrscheinlichkeitsräumen modellieren beispielsweise die unabhängige Wiederholung von Zufallsexperimenten.
Maße auf topologischen Räumen
Falls die Grundmenge
zusätzlich ein topologischer
Raum ist, interessiert man sich vor allem für Maße, die ähnliche
Eigenschaften wie das Lebesgue-Maß oder die Lebesgue-Stieltjes-Maße auf dem
topologischen Raum
mit der Standardtopologie besitzen. Eine einfache Überlegung zeigt, dass die
borelsche σ-Algebra auf
nicht nur von der Menge der
-dimensionalen
Intervalle, sondern auch von den offenen
Teilmengen erzeugt wird. Ist daher
ein Hausdorff-Raum
mit Topologie
(also der Menge der offenen Mengen), so definiert man die borelsche σ-Algebra
auf
als
,
also als kleinste σ-Algebra, die alle offenen Mengen enthält. Natürlich
enthält dann
insbesondere auch alle abgeschlossenen Mengen sowie alle Mengen, die sich als
abzählbare Vereinigungen oder Durchschnitte abgeschlossener bzw. offener Mengen
schreiben lassen.
Borelmaße und Regularität
Ein Maß
auf einem Messraum
,
Hausdorff-Raum und
die borelsche σ-Algebra, heißt Borelmaß, wenn es lokal endlich ist. Das heißt,
jedes
besitzt eine offene
Umgebung, deren Maß endlich ist. Ist
zusätzlich lokalkompakt,
so ist das damit äquivalent, dass alle kompakten
Mengen endliches Maß besitzen.
Ein Radonmaß ist ein
Borelmaß, das von innen regulär ist, das bedeutet, dass für jedes
gilt
.
Ist ein Radonmaß zusätzlich von außen regulär, das heißt, für jedes
gilt
,
so wird es reguläres Borelmaß genannt.
Zahlreiche wichtige Borelmaße sind regulär, es gelten nämlich unter anderem die folgenden Regularitätsaussagen:
- Ist
ein lokalkompakter Hausdorff-Raum mit abzählbarer Basis (zweites Abzählbarkeitsaxiom), dann ist jedes Borelmaß auf
regulär.
- Jedes Borelmaß auf einem polnischen Raum ist regulär.
Wahrscheinlichkeitsmaße auf polnischen Räumen spielen in zahlreichen Existenzfragen der Wahrscheinlichkeitstheorie eine wichtige Rolle.
Haarsches Maß
Der -dimensionale
euklidische Raum ist nicht nur ein lokalkompakter topologischer Raum, sondern
sogar eine topologische
Gruppe bezüglich der üblichen Vektoraddition als Verknüpfung. Das
Lebesgue-Maß
respektiert auch diese Struktur in dem Sinne, dass es invariant gegenüber
Translationen ist: Für alle Borelmengen
und alle
gilt
.
Der Begriff des Haarschen Maßes verallgemeinert diese Translationsinvarianz auf linksinvariante Radonmaße auf hausdorffschen lokalkompakten topologischen Gruppen. Ein solches Maß existiert stets und ist bis auf einen konstanten Faktor eindeutig bestimmt. Das Haarsche Maß ist genau dann endlich, wenn die Gruppe kompakt ist; in diesem Fall kann es also zu einem Wahrscheinlichkeitsmaß normiert werden.>
Haarsche Maße spielen eine zentrale Rolle bei der harmonischen Analyse, in der Methoden der Fourier-Analysis auf allgemeine Gruppen übertragen werden.
Konvergenz von Maßen
Der wichtigste Konvergenzbegriff für Folgen von endlichen Maßen ist die schwache
Konvergenz, die mit Hilfe von Integralen folgendermaßen definiert werden
kann:
Es sei
ein metrischer
Raum. Eine Folge
endlicher Maße auf
heißt schwach konvergent gegen ein endliches Maß
,
in Zeichen
,
wenn für alle beschränkten stetigen
Funktionen
gilt
.
Das Portmanteau-Theorem
gibt einige andere Bedingungen an, die zur schwachen Konvergenz von Maßen
äquivalent sind. Beispielsweise gilt
genau dann, wenn
für alle Borelmengen
mit
gilt, wobei
den topologischen
Rand von
bezeichnet.
Die schwache Konvergenz von Wahrscheinlichkeitsmaßen hat eine wichtige Anwendung bei der Verteilungskonvergenz von Zufallsvariablen, wie sie beim zentralen Grenzwertsatz auftritt. Schwache Konvergenz von Wahrscheinlichkeitsmaßen kann mit Hilfe von charakteristischen Funktionen untersucht werden.
Eine weitere für Anwendungen bedeutende Frage ist, wann man aus Folgen von
Maßen schwach konvergente Teilfolgen auswählen kann, also wie die
relativ
folgenkompakten Mengen von Maßen charakterisiert werden können. Nach dem
Satz
von Prochorow ist eine Menge
endlicher Maße auf einem polnischen Raum
genau dann relativ folgenkompakt, wenn sie beschränkt und straff ist.
Beschränktheit bedeutet hier, dass
ist und Straffheit, dass es zu jedem
ein Kompaktum
gibt mit
für alle
.
Eine Variation der schwachen Konvergenz für Radon-Maße ist die vage Konvergenz, bei der
für alle stetigen Funktionen mit kompaktem Träger gefordert wird.
Anwendungen
Integration
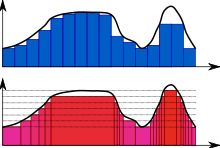
Der Begriff des Maßes ist eng mit der Integration von Funktionen verknüpft. Moderne Integralbegriffe, wie das Lebesgue-Integral und seine Verallgemeinerungen, werden meist aus einer maßtheoretischen Grundlage heraus entwickelt. Der fundamentale Zusammenhang ist dabei die Gleichung
,
für alle ,
wobei ein Maßraum
vorgegeben ist und
die Indikatorfunktion
der messbaren Menge
bezeichnet, also die Funktion
mit
für
und
sonst. Mit Hilfe der gewünschten Linearitäts- und Monotonieeigenschaften lässt
sich die Integration schrittweise zunächst auf einfache Funktionen,
dann auf nicht-negative messbare Funktionen und schließlich auf alle reell- bzw.
komplexwertigen messbaren Funktionen
mit
ausdehnen. Letztere werden
-integrierbar
genannt und ihr Integral
heißt (verallgemeinertes) Lebesgue-Integral bezüglich des Maßes
oder kurz
-Integral.
Dieser Integralbegriff stellt eine starke Verallgemeinerung klassischer Integralbegriffe wie dem Riemann-Integral dar, denn er ermöglicht die Integration von Funktionen auf beliebigen Maßräumen. Das ist wiederum in der Stochastik von großer Bedeutung: Dort entspricht das Integral einer Zufallsvariable bezüglich eines gegebenen Wahrscheinlichkeitsmaßes ihrem Erwartungswert.
Allerdings ergeben sich auch für reelle Funktionen einer reellen Variablen Vorteile gegenüber dem Riemann-Integral. Hier sind vor allem die Konvergenzeigenschaften bei Vertauschung von Grenzwertbildung und Integration zu nennen, die beispielsweise durch den Satz von der monotonen Konvergenz und denSatz von der majorisierten Konvergenz beschrieben werden.
Räume integrierbarer Funktionen
Räume integrierbarer Funktionen spielen als Standardräume der Funktionalanalysis
eine wichtige Rolle. Die Menge aller messbaren Funktionen
auf einem Maßraum
,
die
erfüllen, also
-integrierbar
sind, bildet einen Vektorraum
.
Durch
wird eine Halbnorm auf
definiert. Identifiziert man Funktionen aus diesem Raum miteinander, falls sie
sich nur auf einer Nullmenge voneinander unterscheiden, gelangt man zu einem normierten Raum
.
Eine analoge Konstruktion kann man allgemeiner mit Funktionen durchführen, für
die
für ein
-integrierbar
ist, und gelangt so zu den Lp-Räumen
mit der Norm
.
Ein zentrales Ergebnis, auf das die große Bedeutung dieser Räume in
Anwendungen zurückzuführen ist, ist ihre Vollständigkeit.
Sie sind also für alle
Banachräume. Im wichtigen
Spezialfall
stellt sich die Norm sogar als von einem Skalarprodukt
induziert heraus; es handelt sich bei
daher um einen Hilbertraum.
Völlig analog lassen sich -Räume
komplexwertiger Funktionen definieren. Komplexe
-Räume
sind ebenfalls Hilberträume; sie spielen eine zentrale Rolle in der Quantenmechanik, wo Zustände
von Teilchen durch Elemente eines Hilbertraums beschrieben werden.
Wahrscheinlichkeitstheorie
In der Wahrscheinlichkeitstheorie werden Wahrscheinlichkeitsmaße verwendet,
um zufälligen Ereignissen Wahrscheinlichkeiten zuzuordnen. Zufallsexperimente
werden durch einen Wahrscheinlichkeitsraum
beschrieben, also durch einen Maßraum, dessen Maß
die Zusatzbedingung
erfüllt. Die Grundmenge
,
der Ergebnisraum, enthält die
verschiedenen Ergebnisse,
die das Experiment liefern kann. Die σ-Algebra
besteht aus den Ereignissen,
denen das Wahrscheinlichkeitsmaß
Zahlen zwischen
und
zuordnet.
Bereits der einfachste Fall eines endlichen Ergebnisraums
mit der Potenzmenge als σ-Algebra und der durch
definierten Gleichverteilung
hat zahlreiche Anwendungsmöglichkeiten. Er spielt in der elementaren
Wahrscheinlichkeitsrechnung eine zentrale Rolle zur Beschreibung von
Laplace-Experimenten,
wie dem Werfen eines Würfels und dem Ziehen aus einer Urne, bei denen alle
Ergebnisse als gleich wahrscheinlich angenommen werden.
Wahrscheinlichkeitsmaße werden häufig als Verteilungen
von Zufallsvariablen,
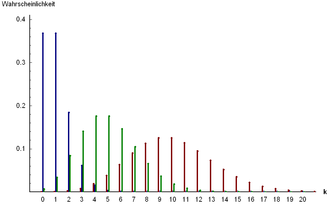
also als Bildmaße, erzeugt. Wichtige Beispiele für Wahrscheinlichkeitsmaße auf
sind die Binomial-
und die Poissonverteilung
sowie die geometrische
und hypergeometrische
Verteilung. Bei den Wahrscheinlichkeitsmaßen auf
mit Lebesgue-Dichte nimmt – unter anderem wegen des zentralen
Grenzwertsatzes – die Normalverteilung
eine herausragende Stellung ein. Weitere Beispiele sind die stetige
Gleichverteilung oder die Gammaverteilung,
die zahlreiche weitere Verteilungen wie etwa die Exponentialverteilung
als Spezialfall umfasst.
Die mehrdimensionale
Normalverteilung ist ebenfalls ein wichtiges Beispiel für
Wahrscheinlichkeitsmaße auf dem -dimensionalen
euklidischen Raum
.
Noch allgemeinere Maßräume spielen in der modernen
Wahrscheinlichkeitstheorie
eine Rolle bei der Konstruktion von stochastischen
Prozessen, wie etwa das Wiener-Maß
auf einem geeigneten Funktionenraum
zur Beschreibung des Wiener-Prozesses
(Brownsche
Bewegung), der auch in der stochastischen
Analysis eine zentrale Stellung einnimmt.
Statistik
Die Grundaufgabe der mathematischen
Statistik besteht darin, aufgrund von Beobachtungsergebnissen zufälliger
Stichproben zu Aussagen über die Verteilung von
Merkmalen in
einer Grundgesamtheit
zu kommen (sog. schließende Statistik). Entsprechend enthält ein statistisches
Modell
nicht nur ein einzelnes als bekannt angenommenes Wahrscheinlichkeitsmaß wie bei
einem Wahrscheinlichkeitsraum, sondern eine ganze Familie
von Wahrscheinlichkeitsmaßen auf einem gemeinsamen Messraum
.
Einen wichtigen Spezialfall stellen die parametrischen Standardmodelle dar, die
dadurch gekennzeichnet sind, dass die Parameter Vektoren aus
sind und alle
eine Dichte bezüglich eines gemeinsamen Maßes besitzen.
Aus der Beobachtung von
soll nun auf den Parameter
und damit auf das Maß
geschlossen werden. Dies geschieht in der klassischen Statistik in der Form von
Punktschätzern, die
mit Hilfe von Schätzfunktionen
konstruiert werden, oder mit Konfidenzbereichen,
die den unbekannten Parameter mit einer vorgegebenen Wahrscheinlichkeit
enthalten. Mit Hilfe statistischer
Tests können außerdem Hypothesen
über das unbekannte Wahrscheinlichkeitsmaß geprüft werden.
Im Gegensatz dazu werden in der bayesschen
Statistik Verteilungsparameter nicht als Unbekannte, sondern selbst als
zufällig modelliert. Dazu wird, ausgehend von einer angenommenen A-priori-Verteilung,
mit Hilfe der durch die Beobachtungsergebnisse gewonnenen Zusatzinformation eine
A-posteriori-Verteilung
des Parameters bestimmt. Diese Verteilungen sind im Allgemeinen
Wahrscheinlichkeitsmaße auf dem Parameterraum ;
für A-priori-Verteilungen kommen jedoch unter Umständen auch allgemeine Maße in
Frage (sog. uneigentliche A-priori-Verteilungen).
Finanzmathematik
Die moderne Finanzmathematik verwendet Methoden der Wahrscheinlichkeitstheorie, insbesondere stochastische Prozesse, zur Modellierung der zeitlichen Entwicklung der Preise von Finanzinstrumenten. Eine zentrale Fragestellung ist die Berechnung fairer Preise von Derivaten.
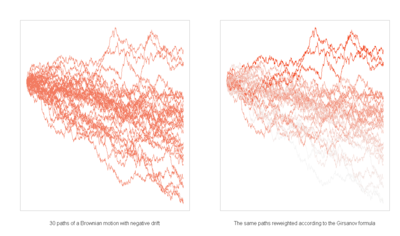
Typisch ist hierbei die Betrachtung verschiedener Wahrscheinlichkeitsmaße auf dem gleichen Messraum: Neben dem realen, durch die Risikobereitschaft der Marktteilnehmer bestimmten Maß werden risikoneutrale Maße verwendet. Faire Preise ergeben sich dann als Erwartungswerte abgezinster Auszahlungen bezüglich eines risikoneutralen Maßes. In arbitragefreien und vollkommenen Marktmodellen ist dabei Existenz und Eindeutigkeit risikoneutraler Maße sichergestellt.
Während sich einfache zeit- und preisdiskrete Modelle bereits mit elementarer Wahrscheinlichkeitsrechnung analysieren lassen, sind insbesondere bei stetigen Modellen wie dem Black-Scholes-Modell und seinen Verallgemeinerungen moderne Methoden der Martingaltheorie und der stochastischen Analysis nötig. Dabei werden als risikoneutrale Maße äquivalente Martingalmaße verwendet. Das sind Wahrscheinlichkeitsmaße, die bezüglich des realen risikobehafteten Maßes eine positive Dichte besitzen und für die der abgezinste Preisprozess ein Martingal (oder allgemeiner ein lokales Martingal) ist. Von Bedeutung ist hierbei zum Beispiel der Satz von Girsanow, der das Verhalten von Wiener-Prozessen bei einem Wechsel des Maßes beschreibt.
Verallgemeinerungen
Das Konzept des Maßes erlaubt zahlreiche Verallgemeinerungen in verschiedene Richtungen. Ein Maß im Sinne dieses Artikels wird daher zur Verdeutlichung in der Literatur manchmal positives Maß oder noch genauer σ-additives positives Maß genannt.
Durch Abschwächung der in der Definition geforderten Eigenschaften erhält man
Funktionen, die in der Maßtheorie als Vorstufen von Maßen betrachtet werden. Der
allgemeinste Begriff ist der einer (nicht-negativen) Mengenfunktion, also
einer Funktion, die den Mengen eines Mengensystems
über einer Grundmenge Werte aus
zuordnet, wobei meist noch gefordert wird, dass die leere Menge den Wert null
bekommt. Ein Inhalt
ist eine endlich additive Mengenfunktion; ein σ-additiver Inhalt heißt
Prämaß. Der Jordan-Inhalt auf den
Jordan-messbaren Teilmengen von
ist ein Anwendungsbeispiel für eine additive Mengenfunktion, die jedoch nicht
σ-additiv ist. Ein Maß ist somit ein Prämaß, dessen Definitionsbereich eine
σ-Algebra ist.
Äußere
Maße, also Mengenfunktionen, die monoton und σ-subadditiv sind,
stellen eine wichtige Zwischenstufe in der Konstruktion von Maßen aus Prämaßen
nach Carathéodory dar: Ein Prämaß auf einem Mengenring wird zunächst zu einem
äußeren Maß auf der ganzen Potenzmenge fortgesetzt, dessen Einschränkung auf
messbare Mengen ein Maß ergibt.
Anders geartete Verallgemeinerungen des Maßbegriffs erhält man, wenn man die
Forderung aufgibt, dass die Werte in
liegen müssen, jedoch die übrigen Eigenschaften beibehält. Bei einem signierten Maß sind
auch negative Werte zugelassen, es kann also Werte im Intervall
(alternativ auch
)
annehmen. Bei komplexen Zahlen als Wertebereich spricht man von einem komplexen Maß. Der
Wert
ist hierbei allerdings nicht zugelassen, das heißt, ein positives Maß ist zwar
stets auch ein signiertes Maß, aber nur endliche Maße können auch als komplexe
Maße aufgefasst werden. Im Gegensatz zu positiven Maßen bilden die signierten
und die komplexen Maße über einem Messraum einen Vektorraum. Solche Räume
spielen nach dem Darstellungssatz
von Riesz-Markow eine wichtige Rolle als Dualräume von Räumen stetiger
Funktionen. Signierte und komplexe Maße lassen sich nach dem Zerlegungssatz von
Hahn und Jordan als Linearkombinationen aus positiven Maßen schreiben. Auch
der Satz
von Radon-Nikodým bleibt für sie gültig.
Eine noch weitergehende Verallgemeinerung stellen Maße mit Werten in beliebigen Banachräumen dar, die sogenannten vektoriellen Maße. Maße auf den reellen Zahlen, deren Werte orthogonale Projektionen eines Hilbertraums sind, sogenannte Spektralmaße, werden im Spektralsatz zur Darstellung selbstadjungierter Operatoren verwendet, was unter anderem in der mathematischen Beschreibung der Quantenmechanik eine wichtige Rolle spielt (siehe auch Positive Operator Valued Probability Measure). Maße mit orthogonalen Werten sind Hilbertraum-wertige Maße, bei denen die Maße disjunkter Mengen orthogonal zueinander sind. Mit ihrer Hilfe können Spektraldarstellungen von stationären Zeitreihen und stationären stochastischen Prozessen angegeben werden.
Zufällige Maße sind Zufallsvariablen, deren Werte Maße sind. Sie werden beispielsweise in der stochastischen Geometrie zur Beschreibung zufälliger geometrischer Strukturen verwendet. Bei stochastischen Prozessen, deren Pfade Sprungstellen aufweisen, wie etwa den Lévy-Prozessen, können die Verteilungen dieser Sprünge durch zufällige Zählmaße dargestellt werden.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 13.01. 2023