Erwartungswert
Der Erwartungswert (selten und doppeldeutig Mittelwert) ist ein Grundbegriff der Stochastik. Der Erwartungswert einer Zufallsvariablen beschreibt die Zahl, die die Zufallsvariable im Mittel annimmt. Er ergibt sich zum Beispiel bei unbegrenzter Wiederholung des zugrunde liegenden Experiments als Durchschnitt der Ergebnisse. Das Gesetz der großen Zahlen beschreibt, in welcher Form genau die Durchschnitte der Ergebnisse bei wachsender Anzahl der Experimente gegen den Erwartungswert streben, oder anders gesagt, wie die Stichprobenmittelwerte bei wachsender Stichprobengröße gegen den Erwartungswert konvergieren.
Er bestimmt die Lokalisation (Lage) der Verteilung
der Zufallsvariablen und ist vergleichbar mit dem empirischen arithmetischen
Mittel einer Häufigkeitsverteilung
in der deskriptiven Statistik. Er berechnet sich als nach Wahrscheinlichkeit
gewichtetes Mittel der Werte, die die Zufallsvariable annimmt. Er muss selbst
jedoch nicht einer dieser Werte sein. Insbesondere kann der Erwartungswert die
Werte
annehmen.
Weil der Erwartungswert nur von der Wahrscheinlichkeitsverteilung abhängt, wird vom Erwartungswert einer Verteilung gesprochen, ohne Bezug auf eine Zufallsvariable. Der Erwartungswert einer Zufallsvariablen kann als Schwerpunkt der Wahrscheinlichkeitsmasse betrachtet werden und wird daher als ihr erstes Moment bezeichnet.
Motivation
Die Augenzahlen beim Würfelwurf können als unterschiedliche Ausprägungen
einer Zufallsvariablen
betrachtet werden. Weil die (tatsächlich beobachteten) relativen Häufigkeiten
sich gemäß dem Gesetz
der großen Zahlen mit wachsendem Stichprobenumfang n den
theoretischen Wahrscheinlichkeiten der einzelnen Augenzahlen annähern, muss der
Mittelwert gegen den Erwartungswert von
streben. Zu dessen Berechnung werden die möglichen Ausprägungen mit ihrer
theoretischen Wahrscheinlichkeit gewichtet.
Wie die Ergebnisse der Würfelwürfe ist der Mittelwert vom Zufall abhängig. Im
Unterschied dazu ist der Erwartungswert eine feste Kennzahl der Verteilung der
Zufallsvariablen .
Die Definition des Erwartungswerts steht in Analogie zum gewichteten Mittelwert von empirisch beobachteten Zahlen. Hat zum Beispiel eine Serie von zehn Würfelversuchen die Ergebnisse 4, 2, 1, 3, 6, 3, 3, 1, 4, 5 geliefert, kann der zugehörige Mittelwert
alternativ berechnet werden, indem zunächst gleiche Werte zusammengefasst und nach ihrer relativen Häufigkeit gewichtet werden:
.
Allgemein lässt der Mittelwert der Augenzahlen in n Würfen sich wie
schreiben, worin
die relative Häufigkeit der Augenzahl
bezeichnet.
Definitionen
Ist eine Zufallsvariable diskret oder besitzt sie eine Dichte, so existieren die folgenden Formeln für den Erwartungswert.
Erwartungswert einer diskreten reellen Zufallsvariablen
Im reellen diskreten Fall errechnet sich der Erwartungswert als die Summe der Produkte aus den Wahrscheinlichkeiten jedes möglichen Ergebnisses des Experiments und den „Werten“ dieser Ergebnisse.
Ist
eine reelle diskrete
Zufallsvariable, die die Werte
mit den jeweiligen Wahrscheinlichkeiten
annimmt (mit
als abzählbarer Indexmenge),
so errechnet sich der Erwartungswert
im Falle der Existenz mit:
Es ist zu beachten, dass dabei nichts über die Reihenfolge der Summation ausgesagt wird (summierbare Familie).
Ist ,
so besitzt
genau dann einen endlichen Erwartungswert
,
wenn die Konvergenzbedingung
erfüllt ist, d. h. die Reihe für den Erwartungswert absolut konvergent ist.
Zur Berechnung ist für nichtnegative Zufallsvariable oft die folgende Eigenschaft hilfreich
Erwartungswert einer reellen Zufallsvariablen mit Dichtefunktion
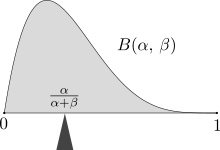
Hat eine reelle Zufallsvariable
eine Wahrscheinlichkeitsdichtefunktion
,
das heißt hat das Bildmaß
diese Dichte
bezüglich dem Lebesgue-Maß
,
so berechnet sich der Erwartungswert im Falle der Existenz als
- (1)
In vielen Anwendungsfällen liegt (im Allgemeinen uneigentliche) Riemann-Integrierbarkeit vor und es gilt:
- (2)
Gleichwertig zu dieser Gleichung ist, wenn
Verteilungsfunktion
von
ist:
- (3)
(2) und (3) sind unter der gemeinsamen Voraussetzung (
ist Dichtefunktion und
ist Verteilungsfunktion von
)
äquivalent, was mit schulgemäßen Mitteln bewiesen werden kann.
Für nichtnegative Zufallsvariablen folgt daraus die wichtige Beziehung zur Zuverlässigkeitsfunktion
Allgemeine Definition
Der Erwartungswert wird entsprechend als das Integral bezüglich
des Wahrscheinlichkeitsmaßes
definiert: Ist
eine P-integrierbare
oder P-quasiintegrierbare
Zufallsvariable von einem Wahrscheinlichkeitsraum
nach
,
wobei
die Borelsche
σ-Algebra über
ist, so wird definiert
.
Die Zufallsvariable
besitzt genau dann einen Erwartungswert, wenn sie quasiintegrierbar
ist, also die Integrale
und
nicht beide unendlich sind, wobei
und
den Positiv- sowie den Negativteil von
bezeichnen. In diesem Fall kann
oder
gelten.
Der Erwartungswert ist genau dann endlich, wenn
integrierbar ist, also die obigen Integrale über
und
beide endlich sind. Dies ist äquivalent mit
In diesem Fall schreiben viele Autoren, der Erwartungswert existiere
oder
sei eine Zufallsvariable mit existierendem Erwartungswert, und schließen
damit den Fall
bzw.
aus.
Erwartungswert von zwei Zufallsvariablen mit gemeinsamer Dichtefunktion
Haben die integrierbaren Zufallsvariablen
und
eine gemeinsame Wahrscheinlichkeitsdichtefunktion
,
so berechnet sich der Erwartungswert einer Funktion
von
und
nach dem Satz
von Fubini zu
Der Erwartungswert von
ist nur dann endlich, wenn das Integral
endlich ist.
Insbesondere ist:
Aus der Randdichte errechnet sich der Erwartungswert wie bei univariaten Verteilungen:
Dabei ist die Randdichte
gegeben durch
Elementare Eigenschaften
Linearität
Der Erwartungswert ist linear,
es gilt also für beliebige, nicht notwendigerweise unabhängige Zufallsvariablen
,
dass
ist. Als Spezialfälle ergeben sich
,
und
.
Die Linearität lässt sich auch auf endliche Summen erweitern:
Die Linearität des Erwartungswertes folgt aus der Linearität des Integrals.
Monotonie
Ist
fast
sicher, und existieren
,
so gilt
.
Wahrscheinlichkeiten als Erwartungswerte
Wahrscheinlichkeiten von Ereignissen
lassen sich auch über den Erwartungswert ausdrücken. Für jedes Ereignis
gilt
,
wobei
die Indikatorfunktion
von
ist.
Dieser Zusammenhang ist oft nützlich, etwa zum Beweis der Tschebyschow-Ungleichung.
Dreiecksungleichung
Es gilt
und
Beispiele
Würfeln
Das Experiment sei ein Würfelwurf.
Als Zufallsvariable
betrachten wir die gewürfelte Augenzahl, wobei jede der Zahlen 1 bis 6 mit einer
Wahrscheinlichkeit von jeweils 1/6 gewürfelt wird.
Wenn beispielsweise 1000 Mal gewürfelt wird, man also das Zufallsexperiment 1000 mal wiederholt und die geworfenen Augenzahlen zusammenzählt und durch 1000 dividiert, ergibt sich mit hoher Wahrscheinlichkeit ein Wert in der Nähe von 3,5. Es ist jedoch unmöglich, diesen Wert mit einem einzigen Würfelwurf zu erzielen.
St. Petersburger Spiel
Das St.
Petersburger Spiel ist ein Spiel, dessen zufälliger Gewinn
einen unendlichen Erwartungswert hat. Es wird eine Münze geworfen. Zeigt sie
Kopf, werden 2 Euro gegeben und das Spiel ist beendet, zeigt sie Zahl, darf
nochmals geworfen werden. Fällt nun Kopf, gibt es 4 Euro und das Spiel ist
beendet, folgt wieder Zahl, so darf ein drittes Mal geworfen werden. Der
Erwartungswert des Gewinnes
ist unendlich:
Zufallsvariable mit Dichte
Gegeben ist die reelle Zufallsvariable
mit der Dichtefunktion
wobei
die Eulersche Konstante bezeichnet.
Der Erwartungswert von
berechnet sich als
Allgemeine Definition
Gegeben sei der Wahrscheinlichkeitsraum
mit
,
die Potenzmenge von
und
für
.
Der Erwartungswert der Zufallsvariablen
mit
und
ist
Da
eine diskrete Zufallsvariable ist mit
und
,
kann der Erwartungswert alternativ auch berechnet werden als
Weitere Eigenschaften
Sigma-Additivität
Sind alle Zufallsvariablen
fast sicher nichtnegativ, so lässt sich die endliche Additivität sogar zur
-Additivität
erweitern:
Erwartungswert des Produkts von n stochastisch unabhängigen Zufallsvariablen
Wenn die Zufallsvariablen
stochastisch voneinander unabhängig
und integrierbar sind, gilt:
insbesondere auch
für
Erwartungswert einer zusammengesetzten Zufallsvariable
Ist
eine zusammengesetzte Zufallsvariable, sprich sind
unabhängige Zufallsvariablen und sind die
identisch verteilt und ist
auf
definiert, so lässt sich
darstellen als
.
Existieren die ersten Momente von ,
so gilt
.
Diese Aussage ist auch als Formel von Wald bekannt.
Monotone Konvergenz
Sind die nichtnegativen Zufallsvariablen
fast sicher punktweise monoton wachsend und konvergieren fast
sicher gegen eine weitere Zufallsvariable
,
so gilt
.
Dies ist der Satz von der monotonen Konvergenz in der wahrscheinlichkeitstheoretischen Formulierung.
Berechnung mittels der kumulantenerzeugenden Funktion
Die kumulantenerzeugende Funktion einer Zufallsvariable ist definiert als
.
Wird sie abgeleitet und an der Stelle 0 ausgewertet, so ist der Erwartungswert:
.
Die erste Kumulante ist also der Erwartungswert.
Berechnung mittels der charakteristischen Funktion
Die charakteristische
Funktion einer Zufallsvariable .
Mit ihrer Hilfe lässt sich durch Ableiten der Erwartungswert der Zufallsvariable
bestimmen:
.
Berechnung mittels der momenterzeugenden Funktion
Ähnlich wie die charakteristische Funktion ist die momenterzeugende Funktion definiert als
.
Auch hier lässt sich der Erwartungswert einfach bestimmen als
.
Dies folgt daraus, dass der Erwartungswert das erste Moment ist und die k-ten Ableitungen der momenterzeugenden Funktion an der 0 genau die k-ten Momente sind.
Berechnung mittels der wahrscheinlichkeitserzeugenden Funktion
Wenn
nur natürliche Zahlen als Werte annimmt, lässt sich der Erwartungswert für auch
mithilfe der wahrscheinlichkeitserzeugenden
Funktion
.
berechnen. Es gilt dann
,
falls der linksseitige Grenzwert existiert.
Beste Approximation
Ist
eine Zufallsgröße auf einem Wahrscheinlichkeitsraum
,
so beschreibt
die beste Approximation an
im Sinne der Minimierung von
,
wobei a eine reelle Konstante ist. Dies folgt aus dem Satz über die beste
Approximation, da
für alle konstanten
ist, wobei
das
-Standardnormalskalarprodukt
bezeichne. Diese Auffassung des Erwartungswertes macht die Definition der Varianz
als minimaler mittlerer quadratischer Abstand sinnvoll.
Erwartungswerte von Funktionen von Zufallsvariablen
Wenn
wieder eine Zufallsvariable ist, so kann der Erwartungswert von
,
statt mittels der Definition, auch mittels der Formel bestimmt werden:
Auch in diesem Fall existiert der Erwartungswert nur, wenn
konvergiert.
Bei einer diskreten Zufallsvariablen wird eine Summe verwendet:
Ist die Summe nicht endlich, dann muss die Reihe absolut konvergieren, damit der Erwartungswert existiert.
Verwandte Konzepte und Verallgemeinerungen
Lageparameter
Wird der Erwartungswert als Schwerpunkt der Verteilung einer Zufallsvariable aufgefasst, so handelt es sich um einen Lageparameter. Dieser gibt an, wo sich der Hauptteil der Verteilung befindet. Weitere Lageparameter sind
- Der Modus: Der Modus gibt an, an welcher Stelle die Verteilung ein Maximum hat, sprich bei diskreten Zufallsvariablen die Ausprägung mit der größten Wahrscheinlichkeit und bei stetigen Zufallsvariable die Maximastellen der Dichtefunktion. Der Modus existiert zwar im Gegensatz zum Erwartungswert immer, muss aber nicht eindeutig sein. Beispiele für nichteindeutige Modi sind bimodale Verteilungen.
- Der Median ist ein weiterer gebräuchlicher Lageparameter. Er gibt an, welcher Wert auf der x-Achse die Wahrscheinlichkeitsdichte so trennt, dass links und rechts des Medians jeweils die Hälfte der Wahrscheinlichkeit anzutreffen ist. Auch der Median existiert immer, muss aber (je nach Definition) nicht eindeutig sein.
Momente
Wird der Erwartungswert als erstes
Moment aufgefasst, so ist er eng verwandt mit den Momenten höherer Ordnung.
Da diese wiederum durch den Erwartungswert in Verknüpfung mit einer Funktion
definiert werden, sind sie gleichsam ein Spezialfall. Einige der bekannten
Momente sind:
- Die Varianz:
Zentriertes zweites Moment,
. Hierbei ist
der Erwartungswert.
- Die Schiefe:
Zentriertes drittes Moment, normiert auf die dritte Potenz der Standardabweichung
. Es ist
.
- Die Wölbung:
Zentriertes viertes Moment, normiert auf
. Es ist
.
Bedingter Erwartungswert
Der bedingte Erwartungswert ist eine Verallgemeinerung des Erwartungswertes auf den Fall, dass Gewisse Ausgänge des Zufallsexperiments bereits bekannt sind. Damit lassen sich bedingte Wahrscheinlichkeiten verallgemeinern und auch die bedingte Varianz definieren. Der bedingte Erwartungswert spielt eine wichtige Rolle in der Theorie der stochastischen Prozesse.
Begriff und Notation
Das Konzept des Erwartungswertes geht auf Christiaan Huygens zurück. In einer Abhandlung über Glücksspiele von 1656, „Van rekeningh in spelen van geluck“ bezeichnet Huygens den erwarteten Gewinn eines Spiels als „het is my soo veel weerdt“. Frans van Schooten verwendete in seiner Übersetzung von Huygens' Text ins Lateinische den Begriff expectatio. Bernoulli übernahm in seiner Ars conjectandi den von van Schooten eingeführten Begriff in der Form valor expectationis.
Im westlichen Bereich wird für den Operator
verwendet, speziell in anglophoner Literatur
.
In der russischsprachigen Literatur findet sich die Bezeichnung .
Die Bezeichnung
betont die Eigenschaft als nicht vom Zufall abhängiges erstes Moment. In der
Physik findet die Bra-Ket-Notation
Verwendung.
Insbesondere wird
statt
für den Erwartungswert einer Größe
geschrieben.
Quantenmechanischer Erwartungswert
Ist
die Wellenfunktion
eines Teilchens in einem bestimmten Zustand
und ist
ein Operator, so ist
der quantenmechanische Erwartungswert von
im Zustand
.
ist hierbei der Ortsraum, in dem sich das Teilchen bewegt,
ist die Dimension von
,
und ein hochgestellter Stern steht für komplexe
Konjugation.
Lässt sich
als formale Potenzreihe
schreiben (und das ist oft so), so wird die Formel verwendet
Der Index an der Erwartungswertsklammer wird nicht nur wie hier abgekürzt, sondern manchmal auch ganz weggelassen.
- Beispiel
Der Erwartungswert des Aufenthaltsorts in Ortsdarstellung ist
Der Erwartungswert des Aufenthaltsorts in Impulsdarstellung ist
wobei wir die Wahrscheinlichkeitsdichtefunktion der Quantenmechanik im
Ortsraum identifiziert haben. In der Physik wird
(rho) statt
geschrieben.
Erwartungswert von Matrizen und Vektoren
Sei
eine stochastische
-Matrix,
mit den stochastischen Variablen
als Elementen, dann ist der Erwartungswert von
definiert als:
.
Falls ein -Zufallsvektor
vorliegt gilt:
.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 03.06. 2020