
Wahrscheinlichkeitsraum
Ein Wahrscheinlichkeitsraum, kurz W-Raum, ist ein grundlegender Begriff aus dem mathematischen Teilgebiet der Wahrscheinlichkeitstheorie. Es handelt sich um ein mathematisches Modell zur Beschreibung von Zufallsexperimenten. Hierbei werden die verschiedenen möglichen Ausgänge des Experiments zu einer Menge zusammengefasst. Teilmengen dieser Ergebnismenge können dann unter bestimmten Voraussetzungen Zahlen zwischen 0 und 1 zugeordnet werden, die als Wahrscheinlichkeiten interpretiert werden.
Der Begriff des Wahrscheinlichkeitsraums wurde in den 1930er Jahren durch den russischen Mathematiker Andrei Kolmogorow eingeführt, dem damit die Axiomatisierung der Wahrscheinlichkeitsrechnung gelang (siehe auch: Kolmogorow-Axiome).
Definition
Formale Definition
Ein Wahrscheinlichkeitsraum ist ein Maßraum
,
dessen Maß
ein Wahrscheinlichkeitsmaß
ist.
Im Einzelnen bedeutet das:
ist eine beliebige nichtleere Menge, genannt die Ergebnismenge. Ihre Elemente heißen Ergebnisse.
ist eine σ-Algebra über der Grundmenge
, also eine Menge bestehend aus Teilmengen von
, die
enthält und abgeschlossen gegenüber der Bildung von Komplementen und abzählbaren Vereinigungen ist. Die Elemente von
heißen Ereignisse. Die σ-Algebra
selbst wird auch Ereignissystem oder Ereignisalgebra genannt.
ist ein Wahrscheinlichkeitsmaß, das heißt eine Mengenfunktion, die den Ereignissen Zahlen zuordnet, derart dass
ist,
für paarweise disjunkte (d.h. sich gegenseitig ausschließende) Ereignisse
gilt (3. Kolmogoroff-Axiom) und
ist (2. Kolmogoroff-Axiom).
Der Messraum
wird auch Ereignisraum genannt. Ein Wahrscheinlichkeitsraum ist also ein
Ereignisraum, auf dem zusätzlich ein Wahrscheinlichkeitsmaß gegeben ist.
Konkretisierung der Definition
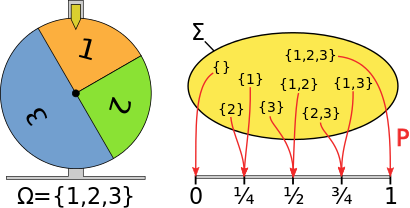
Konkret bedeutet die Definition, dass durch dieses Modell Wahrscheinlichkeit als rein axiomatisch begründetes Konstrukt (also nicht empirisch bestimmt, wie Richard von Mises es versuchte, und auch nicht subjektiv empfunden) messbar gemacht wird. Tragend ist hier unter anderem der Gedanke, die Menge aller möglichen Ausgänge des Zufallsexperiments als sich gegenseitig ausschließende Ergebnisse zu konstruieren. Am Beispiel des Glücksrades wird dies deutlich: Beim Drehen kann das Rad nur in einer einzigen Winkelstellung zu einer gedachten Null-Position stehen bleiben. In der Folge kann dem aber auch nur eine einzige der drei aufgemalten Zahlen 1, 2, 3 zugeordnet werden, das Rad kann nicht im Sektor 1 und gleichzeitig im Sektor 2 stehen bleiben. Ein Mechanismus verhindert, dass es genau auf der Grenze der beiden stehen bleibt. Damit ist das gleichzeitige Eintreffen zweier Elementarereignisse ausgeschlossen, sie sind disjunkt. Dies begründet den Übergang vom Allgemeinen Additionssatz zum speziellen Additionssatz, der dem 3. Kolmogoroffschen Axiom entspricht: Die Wahrscheinlichkeit einer Vereinigung abzählbar vieler inkompatibler (d.h. sich gegenseitig ausschließender) Ereignisse ist gleich der Summe der Wahrscheinlichkeiten der einzelnen Ereignisse.
Klassen von Wahrscheinlichkeitsräumen
Diskrete Wahrscheinlichkeitsräume
Ein Wahrscheinlichkeitsraum heißt ein diskreter
Wahrscheinlichkeitsraum, wenn die Ergebnismenge
endlich oder abzählbar
unendlich ist und die σ-Algebra die Potenzmenge
ist, also
.
Bei manchen Autoren wird bei Einführungen in die Thematik auf die Angabe der
σ-Algebra verzichtet und stillschweigend von der Potenzmenge ausgegangen. Dann
wird nur das Tupel
als diskreter Wahrscheinlichkeitsraum bezeichnet.
Teils werden auch Wahrscheinlichkeitsräume mit beliebiger Grundmenge
diskrete Wahrscheinlichkeitsräume genannt, wenn das Wahrscheinlichkeitsmaß fast
sicher nur Werte in einer höchstens abzählbaren Menge
annimmt, also
gilt.
Endliche Wahrscheinlichkeitsräume
Ein endlicher Wahrscheinlichkeitsraum ist ein Wahrscheinlichkeitsraum,
dessen Grundmenge
endlich ist und dessen σ-Algebra die Potenzmenge ist. Jeder endliche
Wahrscheinlichkeitsraum ist ein diskreter Wahrscheinlichkeitsraum,
dementsprechend wird auch hier teils auf die Angabe der σ-Algebra
verzichtet.
Ist speziell ,
versehen mit der Bernoulli-Verteilung,
also
,
so spricht man von einem Bernoulli-Raum.
Symmetrische Wahrscheinlichkeitsräume
Ein symmetrischer Wahrscheinlichkeitsraum,
auch Laplacescher Wahrscheinlichkeitsraum oder einfach
Laplace-Raum
genannt (nach Pierre-Simon Laplace),
besteht aus einer endlichen Grundmenge .
Als σ-Algebra dient die Potenzmenge
und die Wahrscheinlichkeitsverteilung wird durch eine
Wahrscheinlichkeitsfunktion
definiert als
.
Dies entspricht genau der diskreten Gleichverteilung. Symmetrische Wahrscheinlichkeitsräume sind immer endliche und damit auch diskrete Wahrscheinlichkeitsräume. Demnach wird auch hier gelegentlich auf die Angabe der σ-Algebra verzichtet.
Weitere Klassen
Des Weiteren existieren noch
- induzierter Wahrscheinlichkeitsräume (Bildräume einer Zufallsvariable, versehen mit der Verteilung der Zufallsvariable als Wahrscheinlichkeitsmaß)
- vollständige Wahrscheinlichkeitsräume (vollständige Maßräume mit einem Wahrscheinlichkeitsmaß)
- Produkträume
- Filtrierte Wahrscheinlichkeitsräume: Wahrscheinlichkeitsräume, zusätzlich mit einer Filtrierung versehen.
Beispiele
Diskreter Wahrscheinlichkeitsraum
Ein Beispiel eines diskreten Wahrscheinlichkeitsraumes ist
- die Ergebnismenge der natürlichen Zahlen
. Dann ist jede natürliche Zahl ein Ergebnis.
- Als Ereignissystem wählt man dann wie immer bei höchstens abzählbar
unendlichen Mengen die Potenzmenge
. Dann sind alle Teilmengen der natürlichen Zahlen Ereignisse.
- Als Wahrscheinlichkeitsmaß kann man beispielsweise die Poisson-Verteilung
wählen. Sie weist jeder Zahl
die Wahrscheinlichkeit
für einen echt positiven Parameter
zu
Dann ist
ein diskreter Wahrscheinlichkeitsraum.
Reeller Wahrscheinlichkeitsraum
Ein Beispiel eines reellen Wahrscheinlichkeitsraumes ist
- die Ergebnismenge der nicht-negativen reellen Zahlen
. Dann ist jede nicht-negative reelle Zahl ein Ergebnis.
- Als Ereignissystem die Borelsche
σ-Algebra auf den reellen Zahlen, eingeschränkt auf die nicht-negativen
reellen Zahlen
. Dann sind zum Beispiel alle abgeschlossenen, alle halboffenen und alle offenen Intervalle und deren Vereinigungen, Schnitte und Komplemente Ereignisse.
- Als Wahrscheinlichkeitsmaß zum Beispiel die Exponentialverteilung.
Sie weist jeder Menge
in der Borelschen σ-Algebra die Wahrscheinlichkeit
- für einen Parameter
zu.
Dann ist
ein Wahrscheinlichkeitsraum.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.12. 2020