Orthogonale Gruppe

Die orthogonale Gruppe $\mathrm O(n)$ ist die Gruppe der orthogonalen $(n\times n)$ -Matrizen mit reellen Koeffizienten. Die Verknüpfung der orthogonalen Gruppe ist die Matrizenmultiplikation. Bei der orthogonalen Gruppe handelt es sich um eine Lie-Gruppe der Dimension ${\tfrac {n(n-1)}{2}}$ . Da die Determinante einer orthogonalen Matrix nur die Werte $\pm 1$ annehmen kann, zerfällt $\mathrm O(n)$ in die beiden disjunkten Teilmengen (topologisch: Zusammenhangskomponenten)

die Drehgruppe $\mathrm{SO}(n)$ aller Drehungen (orthogonale Matrizen mit Determinante ) und
${\mathrm O}(n)\setminus {\mathrm {SO}}(n)$ aller Drehspiegelungen (orthogonale Matrizen mit Determinante ).

Die Untergruppe $\mathrm{SO}(n)$ heißt die spezielle orthogonale Gruppe. Insbesondere ist die $\mathrm{SO}(3)$ als die Gruppe aller Drehungen um eine durch den Koordinatenursprung verlaufende Achse im dreidimensionalen Raum von großer Bedeutung in zahlreichen Anwendungen, wie etwa der Computergraphik oder der Physik.

Orthogonale Abbildungen und Matrizen aus algebraischer Sicht

Koordinatenfreie Beschreibung

Ausgehend von einem -dimensionalen euklidischen Vektorraum mit einem Skalarprodukt $\langle \cdot ,\cdot \rangle \colon V\times V\rightarrow \mathbb{R}$ definiert man: Ein Endomorphismus $f\colon V\rightarrow V$ heißt orthogonal, falls das Skalarprodukt erhält, also falls für alle $u, v \in V$

$\langle f(u),f(v)\rangle =\langle u,v\rangle$

gilt. Eine lineare Abbildung erhält genau dann das Skalarprodukt, wenn sie längen- und winkeltreu ist.^[1] Die Menge aller orthogonalen Selbstabbildungen von heißt die orthogonale Gruppe von , geschrieben als ${\mathrm O}(V)$ .

Bezüglich einer Orthonormalbasis von werden orthogonale Endomorphismen durch orthogonale Matrizen dargestellt. Gleichbedeutend hierzu ist folgende Formulierung: Versieht man den $\mathbb {R} ^{n}$ mit dem Standardskalarprodukt, so ist die Abbildung $\mathbb{R} ^{n}\!\ni x\mapsto A\cdot x\in \mathbb{R} ^{n}$ genau dann orthogonal, wenn die Matrix orthogonal ist.

Diagonalisierbarkeit unitärer Matrizen

Jede orthogonale Matrix ist gleichzeitig natürlich auch eine unitäre Matrix mit reellen Koeffizienten. Damit entspricht sie einer unitären Abbildung $f:\mathbb{C} ^{n}\rightarrow \mathbb{C} ^{n}.$ Nach dem Spektralsatz für endlich dimensionale unitäre Räume ist als unitäre Matrix diagonalisierbar. Die dabei auftretenden Diagonalelemente $\lambda _{j}\in \mathbb{C}$ mit $1\leq j\leq n$ sind genau die Eigenwerte von . Diese sind aber notwendig vom Betrag Eins (vgl. unitäre Matrix). Sie lassen sich daher in der Form $\lambda _{j}={\mathrm e}^{{{\mathrm i}\cdot \varphi _{j}}}$ für gewisse, bis auf die Reihenfolge eindeutige Winkel $\varphi _{j}\in [0;2\pi [$ schreiben. Da die Matrix nur reelle Koeffizienten besitzt, treten dabei die nichtreellen Eigenwerte in Paaren zueinander konjugierter komplexer Zahlen auf. Im Reellen ist in der Regel nicht diagonalisierbar, jedoch lässt sich auch hier eine Zerlegung in ein- bzw. zweidimensionale invariante Unterräume angeben.

Auswirkungen auf orthogonale Matrizen

Zu jeder orthogonalen Matrix $A\in {\mathrm O}(n)$ lässt sich eine Drehung des Koordinatensystems $P\in {\mathrm {SO}}(n)$ finden, so dass die Matrix $P^{T}\cdot A\cdot P$ von „beinahe diagonaler“ Gestalt ist:

$P^{T}\cdot A\cdot P={\begin{pmatrix}+1&&&&&&&&\\&\ddots &&&&&&&\\&&+1&&&&&&\\&&&-1&&&&&\\&&&&\ddots &&&&\\&&&&&-1&&&\\&&&&&&D(\varphi _{1})&&\\&&&&&&&\ddots &\\&&&&&&&&D(\varphi _{d})\end{pmatrix}}$

Alle hier nicht angegeben Koeffizienten haben den Wert $0$ . Die auftretenden $(2\times 2)$ -Matrizen $D(\varphi _{j})\in {\mathrm {SO}}(2)$ beschreiben zweidimensionale Drehungen um die Winkel $\varphi _{j}\in \;]0;\pi [\;\cup \;]\pi ;2\pi [$ der Form

$D(\varphi )={\begin{pmatrix}\cos \varphi &-\sin \varphi \\\sin \varphi &\cos \varphi \end{pmatrix}}$

Jedes $\varphi _{j}$ gehört dabei zu einem Paar konjugiert komplexer Eigenwerte ${\mathrm e}^{{\pm {\mathrm i}\cdot \varphi _{j}}}$ . Dabei gilt natürlich p+m+2d=n , falls die Anzahl der Diagonalelemente mit Wert und die Anzahl der Diagonalelemente mit Wert repräsentieren. Offenbar ist genau dann eine Drehung, wenn , die geometrische wie auch algebraische Vielfachheit des Eigenwertes , eine gerade Zahl ist.

Ebene Drehspiegelung

Neben den ebenen Drehungen, die den Matrizen $D(\varphi )\in {\mathrm {SO}}(2)$ entsprechen, sind auch die Drehspiegelungen

$S(\varphi )={\begin{pmatrix}\cos \varphi &\sin \varphi \\\sin \varphi &-\cos \varphi \end{pmatrix}}$

orthogonale Matrizen. Die Eigenwerte von sind und ; folglich handelt es sich um eine Achsenspiegelung die sich nach einer Drehung des Koordinatensystems um ${\tfrac {\varphi }{2}}$ als $\left({\begin{smallmatrix}1&0\\0&-1\end{smallmatrix}}\right)$ schreiben lässt.^[2]

Räumliche Drehung

Nach der oben beschriebenen Normalform lässt sich jede Drehung im Raum durch Wahl einer geeigneten Orthonormalbasis durch eine Matrix

$D_{1}(\varphi )={\begin{pmatrix}1&0&0\\0&\cos \varphi &-\sin \varphi \\0&\sin \varphi &\cos \varphi \end{pmatrix}}$

beschreiben, wobei mit $\varphi \in [0;2\pi [$ auch alle Sonderfälle erfasst werden. Die genannte Matrix $D_{1}(\varphi )$ beschreibt eine Drehung um die $x_{1}$ -Achse. Insbesondere verfügt jede echte räumliche Drehung über eine Drehachse. Fischer^[3] verdeutlicht dies am Beispiel eines Fußballes auf dem Anstoßpunkt: Nach dem ersten Tor gibt es zwei sich gegenüberliegende Punkte auf dem Ball, die jetzt exakt genauso zum Stadion ausgerichtet sind, wie zu Beginn des Spieles. Der Winkel $\varphi$ ist aufgrund des orientierungserhaltenden Charakters der zugelassenen Transformationsmatrizen $P\in {\mathrm {SO}}(3)$ eindeutig festgelegt; dies geht mit der aus dem Alltag bekannten Erfahrung einher, dass es – zumindest theoretisch – stets feststeht, in welche Richtung man eine Schraube drehen muss, um diese fester anzuziehen.

Räumliche Drehspiegelung

Nach der oben beschriebenen Normalform lässt sich jede Drehspiegelung im Raum durch Wahl einer geeigneten Orthonormalbasis durch eine Matrix

${\begin{pmatrix}-1&0&0\\0&\cos \varphi &-\sin \varphi \\0&\sin \varphi &\cos \varphi \end{pmatrix}}$

beschreiben, wobei mit $\varphi \in [0;2\pi [$ auch alle Sonderfälle erfasst werden. Auch hier ist der Winkel $\varphi$ eindeutig, sofern man die Orientierung des Raumes nicht umkehrt.

Eine doppelte Drehung im vierdimensionalen Raum

Im vierdimensionalen Raum ist eine gleichzeitige Drehung mit zwei unabhängigen Drehwinkeln möglich:

$D(\varphi ,\psi )={\begin{pmatrix}D(\varphi )&0\\0&D(\psi )\end{pmatrix}}\in {\mathrm {SO}}(4)$

Vertauscht man bei einer zweidimensionalen Drehung $D(\varphi )$ die beiden Basisvektoren, so erhält man die Drehung $D(2\pi -\varphi )$ . Das ist nicht verwunderlich, hat man doch gleichzeitig die Orientierung der Ebene verändert. Vertauscht man nun im vorliegenden Beispiel gleichzeitig den ersten mit dem zweiten wie auch den dritten mit dem vierten Basisvektor, so bleibt die Orientierung erhalten, aber aus $D(\varphi ,\psi )$ wird $D(2\pi -\varphi ,2\pi -\psi )$ .

Die Orthogonale Gruppe als Lie-Gruppe

Ausgehend vom linearen Raum $\mathbb{R} ^{{n\times n}}$ aller Matrizen gelangt man zur Untermannigfaltigkeit $\mathrm O(n)$ durch die Forderung, dass die Matrix orthogonal ist, d.h. $A^{T}\cdot A=E$ gilt. Da orthogonale Matrizen insbesondere invertierbar sind, ist $\mathrm O(n)$ eine Untergruppe der allgemeinen linearen Gruppe $\mathrm {GL} (n,\mathbb {R} )$ .

Topologische Eigenschaften

Wie die allgemeine lineare Gruppe besteht auch die orthogonale Gruppe aus zwei Zusammenhangskomponenten: Matrizen mit positiver bzw. negativer Determinante im Fall der reellen ${\mathrm {GL}}(n)$ ; $\mathrm{SO}(n)$ und die Menge der orthogonalen Matrizen mit Determinante im Falle der $\mathrm O(n)$ . Serge Lang^[4] gibt einen eleganten Beweis für den Wegzusammenhang der $\mathrm{SO}(n)$ : Man verbinde die Einheitsmatrix mit einer gegebenen Drehung durch einen Weg innerhalb der ${\mathrm {GL}}(n)$ . Wendet man auf jeden Punkt dieses Weges nun das Gram-Schmidtsche Orthogonalisierungsverfahren an, so erhält man einen Weg, der ganz in der $\mathrm{SO}(n)$ verläuft. Da die Multiplikation mit der Diagonalmatrix ${\mathrm {diag}}(-1,1,\ldots ,1)$ einen Diffeomorphismus von $\mathrm{SO}(n)$ mit seinem Komplement in der $\mathrm O(n)$ liefert, ist auch Letzteres zusammenhängend.

Weiterhin sind $\mathrm{SO}(n)$ wie $\mathrm O(n)$ natürlich kompakt. Es handelt sich um eine abgeschlossene Teilmenge der Einheitskugel bezüglich der Spektralnorm im $\mathbb {R} ^{n\times n}$ .

Operation der SO(n) auf der Einheitssphäre

Die $\mathrm{SO}(n)$ operiert in natürlicher Weise auf dem $\mathbb {R} ^{n}$ . Da orthogonale Abbildungen längentreu sind, sind die Bahnen dieser Operation genau die Sphären um den Ursprung. Die Operation schränkt also zu einer transitiven Operation auf der Einheitssphäre $S^{{\,n-1}}\subset \mathbb{R} ^{n}$ ein. Die zugehörige Isotropiegruppe des kanonischen Einheitsvektors e_n der Standardbasis des $\mathbb {R} ^{n}$ besteht genau aus der ${\mathrm {SO}}(n-1)$ , aufgefasst als Untergruppe der $\mathrm{SO}(n)$ mit einer an der Matrix-Position (n,n) . Man erhält somit die kurze exakte Sequenz

${\mathrm {SO}}(n-1)\rightarrow {\mathrm {SO}}(n)\rightarrow S^{{\,n-1}}$

beziehungsweise das Hauptfaserbündel (vgl. auch Faserbündel)

${\mathrm {SO}}(n)/{\mathrm {SO}}(n-1)\rightarrow S^{{\,n-1}}$ .

Hieraus lässt sich induktiv folgern, dass die Fundamentalgruppe der $\mathrm{SO}(n)$ für $n\geq 3$ zu $\mathbb{Z } /2\mathbb{Z }$ isomorph ist.^[5] Sie ist damit ähnlich „verdreht“ wie das Möbiusband. Die Fundamentalgruppe der Kreisgruppe ${\mathrm {SO}}(2)$ ist $\mathbb {Z}$ (vgl. auch Windungszahl), da die ${\mathrm {SO}}(2)$ topologisch dem Einheitskreis $S^{{\,1}}\subset \mathbb{R} ^{2}$ entspricht.

Die Lie-Algebra zur O(n) und SO(n)

Die Lie-Algebra ${\mathfrak {o}}(n)$ besteht genau aus den schiefsymmetrischen Matrizen, die Lie-Algebra $\mathfrak{so}(n)$ , also der Tangentialraum der $\mathrm{SO}(n)$ im Punkt der Einheitsmatrix $E_{n}$ , besteht genau aus den schiefsymmetrischen Matrizen^[6], die zugleich spurlos sind, was im Reellen bereits durch die Schiefsymmetrie impliziert ist. Daher sind beide Lie-Algebren gleich

${\mathfrak {o}}(n)={\mathfrak {so}}(n)=\left\{A\in {\mathit {Mat}}(n,\mathbb {C} ):{A}^{T}=-A\right\}$ .

Ist also $A=-A^{T}$ schiefsymmetrisch, so liefert die Exponentialabbildung für Matrizen die zugehörige Einparametergruppe

$\alpha ^{A}\colon \mathbb{R} \ni t\mapsto \exp(t\cdot A)\in {\mathrm {SO}}(n)\,.$

In allgemeinen Lie-Gruppen ist die Exponentialabbildung nur lokal surjektiv, von einer Umgebung der Null auf eine Umgebung der Eins; die Exponentialabbildung von $\mathfrak{so}(n)$ nach $\mathrm{SO}(n)$ dagegen ist tatsächlich (global) surjektiv.

Offensichtlich ist eine schiefsymmetrische Matrix durch die ${\tbinom n2}={\tfrac {n\cdot (n-1)}{2}}$ Einträge oberhalb der Hauptdiagonale eindeutig bestimmt. Damit ist die Dimension der $\mathrm{SO}(n)$ ebenfalls geklärt.

Im Fall n=2 haben die Matrizen der zugehörigen Lie-Algebren die einfache Form

${\mathfrak {o}}(2)={\mathfrak {so}}(2)=\left\{{\begin{pmatrix}0&\lambda \\-\lambda &0\end{pmatrix}}:\lambda \in \mathbb {R} \right\}=\operatorname {span} {\begin{pmatrix}0&1\\-1&0\end{pmatrix}}=\operatorname {span_{\mathbb {R} }} (i\sigma _{2})$

wobei $\sigma _{2}$ die zweite Pauli-Matrix ist.

Im Fall n=3 ist die zugehörige Lie-Algebra $\mathfrak{so}(3)$ isomorph zum $\mathbb {R} ^{3}$ mit dem Kreuzprodukt als Lie-Klammer. Zum Nachweis muss man lediglich den Kommutator zweier generischer, also mit je drei freien Variablen gebildeter, schiefsymmetrischer Matrizen berechnen und das Ergebnis mit der Formel für das Kreuzprodukt vergleichen.

Dreidimensionale Drehungen

Eulerwinkel $\scriptstyle \alpha ,\beta$ und $\scriptstyle \gamma$ : Das blaue Dreibein soll in das rote überführt werden. Überführt man die rote wie die blaue x-Achse durch Drehungen um die jeweilige z-Achse auf die grüne „Knotenlinie“, so fehlt nur noch eine Drehung um die grüne Achse.

Beschreibung durch Achse und Winkel

Eine Drehung im dreidimensionalen Raum lässt sich durch die Angabe einer Drehachse, also eines Vektors $v\in S^{{\,2}}$ der Länge Eins auf der Einheitssphäre, und eines Drehwinkels $\varphi \in [0;2\pi ]$ beschreiben. Im Sonderfall $\varphi=0$ erhält man die identische Abbildung; für andere Winkel, auch im Fall einer Geradenspiegelung mit $\varphi =\pi$ , ist die Achse eindeutig festgelegt. Durch Wechsel der Orientierung der Drehachse lässt sich eine Drehung um $\varphi$ auch als eine Drehung mit Winkel $2\pi -\varphi$ auffassen.

Die zugehörige Drehung $D(v,\varphi )$ lässt sich durch eine zugehörige Drehmatrix explizit angegeben (siehe dort).

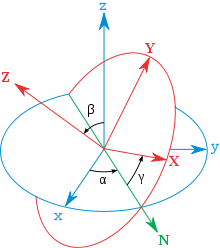
Beschreibung durch Eulersche Winkel

Auf Leonhard Euler geht eine andere Beschreibung von Drehungen über drei Winkel, die sogenannten Eulerschen Winkel, zurück. Ausgehend von der Standardbasis $e_{x},\,e_{y},\,e_{z}$ zeigt Euler, dass sich jede Drehung als

$D=D(e_{z},\gamma )\circ D(e_{x},\beta )\circ D(e_{z},\alpha )$

schreiben lässt.^[8]

Dabei sind die drei Winkel mit der Einschränkung $\beta \in [-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}}[$ bis auf singuläre Bereiche eindeutig bestimmt: etwa für $\beta=0$ reicht natürlich einer der beiden anderen Winkel völlig aus.

Eulerwinkel werden in der Physik gerne verwendet; auch die Beschreibung der Bahnen von Planeten oder Asteroiden durch die sogenannten Bahnelemente beruht hierauf.

Beschreibung mittels Quaternionen

$\times$

Die Hamiltonschen Quaternionen $\mathbb H$ gestatten eine sehr elegante Beschreibung räumlicher Drehungen. Die Quaternionen bilden eine vierdimensionale Algebra über den reellen Zahlen. Als Basis verwendet man vier besondere Quaternionen, nämlich 1,i,j und . Hierbei ist $k=i\cdot j=-j\cdot i$ (die Multiplikation ist also nicht kommutativ) und es gelten die folgenden von William Rowan Hamilton angegebenen Rechenregeln: $i^{2}=j^{2}=k^{2}=-1$ . Mit dieser Multiplikationsvorschrift – verschiedene, mathematisch exakte Konstruktionen der Quaternionenalgebra finden sich hier – wird $\mathbb H$ sogar zu einem Schiefkörper: Zu jeder von null verschiedenen Quaternion lässt sich eine inverse Quaternion $q^{{-1}}$ berechnen, für die $q\cdot q^{{-1}}=1=q^{{-1}}\cdot q$ gilt.^[9]

Eine Quaternion heißt rein, wenn sie sich als Linearkombination der drei Basisvektoren i, j und schreiben lässt. Vermöge der linearen Einbettung

$\mathbb{R} ^{3}\ni v\mapsto {\hat v}\in {\mathbb H}$

mit ${\hat e}_{x}={\mathrm i}$ , ${\hat e}_{y}={\mathrm j}$ und ${\hat e}_{z}={\mathrm k}$ identifizieren wir den $\mathbb {R} ^{3}$ mit den reinen Quaternionen. Nun lässt sich die Multiplikationsregel für Quaternionen geometrisch deuten: Das Produkt zweier reiner Quaternionen ${\hat v}$ und ${\hat w}$ ist zwar nicht wieder rein, aber es gilt

${\hat v}\cdot {\hat w}=v\cdot w\cdot 1+\widehat {v\times w}$

Der reine Anteil des Produktes zweier reiner Quaternionen entspricht also ihrem Vektorprodukt, während der skalare Anteil (der Koeffizient vor dem Basisvektor ) ihr Skalarprodukt darstellt.

Um nun die Drehung $D(v,\varphi )$ durch eine Quaternion zu beschreiben, benötigen wir zunächst einen Winkel $\psi$ , dessen Doppeltes, $2\psi ,$ dem gegebenen $\varphi$ entspricht. Neben $\psi ={\tfrac {\varphi }{2}}$ leistet dies auch $\psi ={\tfrac {\varphi }{2}}+\pi$ . Wir betrachten nun die Quaternion

$q:=\cos \psi +{\hat v}\cdot \sin \psi$

Diese Quaternion hat Länge Eins (bezüglich des Standardskalarprodukts in $\mathbb {R} ^{4}$ ) und ihr Inverses lautet

$q^{{-1}}=\cos \psi -{\hat v}\cdot \sin \psi$

Nimmt man nun eine beliebige reine Quaternion ${\hat {x}}$ , so lässt sich leicht nachweisen, dass die mit konjugierte Quaternion

${\hat y}:=q\cdot {\hat x}\cdot q^{{-1}}$

wieder eine reine Quaternion ist (wodurch sie sich erst als ${\hat {y}}$ für genau ein $y\in \mathbb{R} ^{3}$ darstellen lässt). Dabei gilt nun

$y=D(v,\varphi )(x)$

Mit anderen Worten: die Konjugation mit wirkt auf den reinen Quaternionen wie die Drehung $D(v,\varphi )$ .

Universelle Überlagerung der SO(3)

Eine zweiblättrige Überlagerung: Hier am Beispiel der komplexen Quadratwurzel dargestellt. Über jedem Punkt der punktierten komplexen Zahlenebene liegen genau zwei Punkte des überlagernden Raumes. Zu einer komplexen Zahl $\scriptstyle z\neq 0$ lassen sich genau zwei Zahlen $\scriptstyle w$ mit $\scriptstyle w^{2}=z$ finden. Bei der zeichnerischen Darstellung im dreidimensionalen Raum ist eine Selbstdurchdringung der Fläche leider unvermeidbar.

Die oben beobachtete Zweideutigkeit bei der Wahl von $\psi$ geht einher mit den beiden möglichen Vektoren zur Beschreibung der Achse: Eine bestimmte Drehung lässt sich genau durch zwei zueinander inverse Einheitsquaternionen beschreiben. Rein topologisch handelt es sich bei der Menge der Einheitsquaternionen ${\mathrm {Spin}}(1)\subset {\mathbb H}$ offenbar um die dreidimensionale Einheitssphäre $S^{{\,3}}\subset \mathbb{R} ^{4}\cong {\mathbb H}$ im vierdimensionalen Raum. Die Quaternionenmultiplikation verleiht ihr eine Lie-Gruppenstruktur. Als solche ist sie isomorph zur speziellen unitären Gruppe $\mathrm{SU}(2)$ . Wie im vorangegangenen Abschnitt diskutiert, liefert die Konjugation mit einer Einheitsquaternion $q\in {\mathrm {Spin}}(1)$ eine Drehung. Offenbar handelt es sich hierbei um einen surjektiven Gruppenhomomorphismus, der in einer genügend kleinen Umgebung von einen Diffeomorphismus auf sein Bild in $\mathrm{SO}(3)$ darstellt. Mit anderen Worten, die Abbildung

${\mathrm {Spin}}(1)\rightarrow {\mathrm {SO}}(3)$

ist eine zweiblättrige Überlagerung. Da ${\mathrm {Spin}}(1)=S^{{\,3}}$ einfach zusammenhängend ist, handelt es sich um die universelle Überlagerung der $\mathrm{SO}(3)$ .

Um die anschauliche Bedeutung dieser universellen Überlagerung zu verstehen, kehren wir zu dem bereits oben betrachteten Fußball zurück. Durch geeignete Markierungen auf dem Ball lässt sich prinzipiell zu jedem Zeitpunkt die Drehung bestimmen, die der Ball seit dem Anstoß vollzogen hat. Dies ergibt einen stetigen Weg durch die $\mathrm{SO}(3)$ , der bei der Einheitsmatrix beginnt. Beschreibt man die Einheitsmatrix etwa durch das Einselement von ${\mathrm {Spin}}(1)$ (alternativ könnte man das antipodal gegenüberliegende Element in ${\mathrm {Spin}}(1)=S^{{\,3}},$ also $-1\in {\mathbb H}$ verwenden), so lässt sich nun der gesamte Weg in stetiger Weise zu einem Weg durch die ${\mathrm {Spin}}(1)$ liften. Selbst wenn man den Ball zu Beginn der zweiten Halbzeit den Markierungen entsprechend exakt gleich orientiert wieder auf dem Anstoßpunkt positioniert (damit endet der Weg durch die $\mathrm{SO}(3)$ wieder im Punkt der Einheitsmatrix), so ist nicht garantiert, dass auch der geliftete Weg wieder bei der Eins-Quaternion $1\in {\mathbb H}$ angelangt ist. Mit einer Wahrscheinlichkeit von $50\%$ endet Letzterer vielmehr in der ; dann müsste man den Ball noch einmal um 360° bezüglich einer beliebig gewählten Achse drehen, um auch den gelifteten Weg in seinem Ausgangspunkt enden zu lassen. Da es keine höherblättrige Überlagerung der $\mathrm{SO}(3)$ gibt, ist es nicht möglich, die allgemeine Drehungen im Raum in konsistenter Weise noch feinstufiger zu erfassen.

Bemerkenswerterweise verwendet man in der Quantenmechanik die $\mathrm{SU}(2)$ und nicht die $\mathrm{SO}(3)$ als Zustandsraum zur Beschreibung des Spins eines Teilchens.

Topologie der SO(3)

Jede Faser der soeben beschrieben Überlagerung

$S^{{\,3}}\mapsto {\mathrm {SO}}(3)$

besteht aus zwei Antipodenpunkten (entsprechend den beiden Möglichkeiten für die Wahl von $\psi$ mit $2\psi =\varphi \,{\mathrm {mod}}\,2\pi \mathbb{Z }$ ) der $S^{{\,3}}$ . Folglich ist die $\mathrm{SO}(3)$ homöomorph zum Quotienten von $S^{{\,3}}$ bei Identifizierung gegenüberliegender Punkte. Dies ergibt aber genau den dreidimensionalen reell-projektiven Raum $\mathbb{R} P^{3}$ .

Endliche Untergruppen der SO(3)

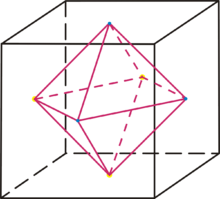
Wenn eine Drehung den Würfel erhält, so erhält sie auch das duale Oktaeder.

Die endlichen Untergruppen der $\mathrm{SO}(3)$ stehen in einem engen Zusammenhang mit Raumkörpern, die eine endliche Zahl von Symmetrien aufweisen. Da bei einer beliebigen Drehung etwa eines Würfels im Raum die zugehörige Untergruppe mit ebendieser Drehung konjugiert wird, interessiert man sich nur für die Konjugationsklassen der endlichen Untergruppen der $\mathrm{SO}(3)$ . Diese sind:

Die zyklische Gruppen $C_{n}$ für $n\geq 1$ , erzeugt von einer Drehung um den -ten Teil eines Vollwinkels $2\pi$ ; für $n\geq 3$ sind sie Teil der vollen Drehgruppe eines geraden Prismas über einem regulären -Eck.
Die volle Drehgruppe eines solchen Prismas. Sie enthält neben der bereits beschriebenen $C_{n}$ auch diejenigen Drehungen, die auf dem regelmäßigen -Eck wie Achsenspiegelungen wirken, aber durch gleichzeitiges Spiegeln an der Trägerebene des -Ecks zu Drehungen des Raums werden. Es handelt sich um die Diedergruppen $D_{n}$ der Ordnung (formal für $n\geq 2$ ; geometrische Deutung für $n\geq 3$ ).
Die volle Drehgruppe ${\mathbb T}$ eines regulären Tetraeders. Sie ist isomorph zur alternierenden Gruppe $A_{4}$ der Ordnung .
Die volle Drehgruppe $\mathbb O$ eines regulären Oktaeders, die sogenannte Oktaedergruppe der Ordnung . Sie ist gleichzeitig für den zum Oktaeder dualen Würfel zuständig. Sie ist isomorph zur symmetrischen Gruppe $S_{4}$ .
Die volle Drehgruppe $\mathbb I$ eines regulären Ikosaeders (siehe Ikosaedergruppe der Ordnung . Sie beschreibt zugleich die Drehungen des Dodekaeders und ist isomorph zur alternierenden Gruppe .

Literatur

Theodor Bröcker, Tammo tom Dieck: Representations of Compact Lie Groups (= Graduate Text im Mathematics. Bd. 98). Springer, New York NY u. a. 1985, ISBN 3-540-13678-9.
Gerd Fischer: Lineare Algebra (= Vieweg-Studium. Bd. 17). 5. Auflage. Vieweg, Braunschweig u. a. 1979, ISBN 3-528-17217-7.
Serge Lang: Linear Algebra. 2nd edition. Addison-Wesley, Reading MA u. a. 1971.
Hermann Weyl: The classical Groups. Their invariants and representations (= Princeton Mathematical Series. Bd. 1, ISSN 0079-5194). 2. edition, with supplement, reprinted. Princeton University Press u. a., Princeton NJ 1953.

Anmerkungen

↑ Das Skalarprodukt eines euklidischen Vektorraums lässt sich sogar aus dem zugehörigen Längenbegriff alleine rekonstruieren. Vgl. Polarisationsformel.
↑ Es handelt sich bei $\scriptstyle S(\varphi )$ um eine Spiegelung an der x-Achse gefolgt von einer Drehung um $\scriptstyle \varphi$ . Dabei bleibt ein um $\scriptstyle \varphi /2$ zur x-Achse gedrehter Vektor fest.
↑ Vgl. G. Fischer: Lineare Algebra. 5. Auflage. 1979, S. 205.
↑ Vgl. S. Lang: Linear Algebra. 2nd edition. 1971, VI, §2. Zitiert nach Bröcker, tom Dieck: Representations of Compact Lie Groups. 1985, S. 5.
↑ Vgl. Bröcker, tom Dieck: Representations of Compact Lie Groups. 1985, S. 36 und S. 61.
↑ Vgl. Bröcker, tom Dieck: Representations of Compact Lie Groups. 1985, S. 20. Wenn man beispielsweise die Funktion $\scriptstyle \mathbb{R} \ni t\mapsto D(t)\in {\mathrm {SO(2)}}$ mit der oben definierten zweidimensionalen Drehung $\scriptstyle D(\varphi )$ in $\scriptstyle t=0$ ableitet, so erhält man die schiefsymmetrische Matrix $\left({\begin{smallmatrix}0&-1\\1&0\end{smallmatrix}}\right)$ .
↑ Die insgesamt $\scriptstyle n^{2}$ Gleichungen, die die Orthogonalität einer Matrix sicherstellen, haben also nur (bzw. beim zweiten Nachdenken tatsächlich) den Rang $\scriptstyle n^{2}-n\cdot {\tfrac {n-1}{2}}=n\cdot {\tfrac {n+1}{2}}$ .
↑ Die Zeichnung stimmt insofern nicht mit der Zerlegung von D überein, als in der Zeichnung das Koordinatensystem gedreht wird, während in der mathematischen Beschreibung das Koordinatensystem raumfest bleibt.
↑ Es ist nämlich $\scriptstyle (a+bi+cj+dk)\cdot (a-bi-cj-dk)=a^{2}+b^{2}+c^{2}+d^{2}$ ein reelles Vielfaches der $\scriptstyle 1$ .

Basierend auf einem Artikel in:

Wikipedia.de