Diedergruppe

Diese Schneeflocke hat die Symmetriegruppe eines regelmäßigen Sechsecks

In der Gruppentheorie ist die Diedergruppe $D_{n}$ als semidirektes Produkt $\mathbb {Z} /n\mathbb {Z} \rtimes _{g\mapsto g^{-1}}\mathbb {Z} /2\mathbb {Z}$ erklärt (siehe unten) und enthält daher genau Elemente. Für $n \ge 3$ ist diese Gruppe isomorph zur Isometriegruppe eines regelmäßigen Polygons in der Ebene. Sie ist dann nicht-abelsch und enthält Drehungen und Achsenspiegelungen. Ihr Name leitet sich vom Wort Dieder (Silbentrennung: Di-eder, Aussprache [diˈeːdər]) (griechisch: Zweiflächner) für regelmäßige -Ecke ab. Diese Gruppen treten häufig in der Geometrie und Gruppentheorie auf, werden von zwei Spiegelungen (Elementen der Ordnung ) erzeugt und sind damit die einfachsten Beispiele von Coxeter-Gruppen.

Bezeichnungen

Es gibt für Diedergruppen zwei abweichende Bezeichnungen. In der Geometrie schreibt man üblicherweise $D_{n}$ , um den Zusammenhang mit dem regelmäßigen -Eck zu unterstreichen. In der Gruppentheorie schreibt man oft auch $D_{2n}$ , um stattdessen die Ordnung hervorzuheben. Diese Zweideutigkeit lässt sich jedoch leicht durch eine erläuternde Ergänzung beheben. In diesem Artikel steht $D_{n}$ für die Diedergruppe mit Elementen.

Definition

Die Diedergruppe $D_{n}$ kann für $n \ge 3$ als die Isometriegruppe eines regelmäßigen -Ecks in der Ebene definiert werden. Diese besteht aus Drehungen und Spiegelungen, hat also insgesamt Elemente. Die Isometrien bezeichnet man auch als Symmetrietransformationen. Als Verknüpfung der Gruppe $D_{n}$ dient die Hintereinanderausführung von Symmetrietransformationen.

In den Fällen n=1 und n=2 führt die geometrische Definition jedoch zu anderen Gruppen. Daher ist hier die algebraische Definition über das semidirekte Produkt $\mathbb {Z} /n\mathbb {Z} \rtimes \mathbb {Z} /2\mathbb {Z}$ vorzuziehen (dabei ist in dem semidirekten Produkt die Operation von $\mathbb {Z} /2\mathbb {Z}$ auf $\mathbb {Z} /n\mathbb {Z}$ durch Inversion gegeben). Diese algebraische Definition gilt für alle $n\geq 1$ .

Beispiele

Ein Beispiel ist die Diedergruppe D_3 der Kongruenzabbildungen eines gleichseitigen Dreiecks auf sich, die isomorph zur symmetrischen Gruppe $S_{3}$ ist. $D_{4}$ ist entsprechend die Symmetriegruppe des Quadrats unter Spiegelungen und Drehungen.

$D_{2}$ ist isomorph zur Kleinschen Vierergruppe und ist die Symmetriegruppe (bestehend nur aus den beiden Spiegelungen, der Drehung um 180° und der Identität) von den vier Ecken eines Quadrats, bei dem nur die rechte und linke Seite eingezeichnet sind (also zwei Zweiecke). $D_{1}$ ist die Symmetriegruppe eines Zweiecks.

$D_{2}$ ist auch die Symmetriegruppe eines nicht gleichseitigen Rechtecks oder einer nicht gleichwinkligen Raute. $D_{1}$ ist auch die Symmetriegruppe eines gleichschenkligen Dreiecks, das nicht gleichseitig ist.

Die folgende Grafik illustriert die Diedergruppe D_8 anhand der Drehungen und Spiegelungen eines Stoppschildes: Die erste Zeile zeigt die acht Drehungen, die zweite Zeile die acht Spiegelungen.

Matrix-Darstellung

Wir betrachten ein ebenes regelmäßiges -Eck. Seinen Mittelpunkt wählen wir als Nullpunkt eines Koordinatensystems, irgendeine seiner Symmetrieachsen als -Achse und die Normale dazu (in üblicher Orientierung, sodass sich ein Rechtssystem ergibt) als -Achse. Die Diedergruppe $D_{n}$ lässt sich dann leicht als Matrixgruppe darstellen. Hierzu sei $r_{k}$ die Drehung um um den Winkel $\alpha _{k}:=k\cdot 2\pi /n$ und s_k die Spiegelung an der Geraden durch , die im Winkel $\alpha_k/2=k\cdot \pi/n$ gegenüber der positiven -Achse geneigt ist. Als Matrizen schreiben sich diese Transformationen dann so:

$r_{k}={\begin{pmatrix}\cos(\alpha _{k})&-\sin(\alpha _{k})\\\sin(\alpha _{k})&\cos(\alpha _{k})\end{pmatrix}}\qquad {\text{und}}\qquad s_{k}={\begin{pmatrix}\cos(\alpha _{k})&\sin(\alpha _{k})\\\sin(\alpha _{k})&-\cos(\alpha _{k})\end{pmatrix}}$

Hierbei fallen folgende Relationen auf:

$r_{k+n}=r_k$ und $s_{k+n}=s_k$ . Daher können wir uns auf $k=0,1,2,\dotsc ,n-1$ beschränken.
$r_{0}$ , die Drehung um den Winkel $0$ , ist die Identität.
$r_{1}$ ist die Drehung um den Winkel $2\pi/n$ und es gilt für alle .
$s_{0}$ ist die Spiegelung an der -Achse und es gilt für alle .

Wenn ungerade ist, dann verläuft jede der Spiegelachsen durch einen Eckpunkt und den Mittelpunkt der gegenüberliegenden Seite. Für gerades gibt es hingegen zwei Arten von Spiegelachsen, durch zwei gegenüberliegende Eckpunkte oder durch zwei gegenüberliegende Seitenmittelpunkte.

In dieser Darstellung schreiben sich zum Beispiel die acht Elemente der Diedergruppe $D_{4}$ wie folgt:

$\begin{align} r_0 &= \bigl(\begin{smallmatrix}1&0\\0&1\end{smallmatrix}\bigr), & r_1 &= \bigl(\begin{smallmatrix}0&-1\\1&0\end{smallmatrix}\bigr), & r_2 &= \bigl(\begin{smallmatrix}-1&0\\0&-1\end{smallmatrix}\bigr), & r_3 &= \bigl(\begin{smallmatrix}0&1\\-1&0\end{smallmatrix}\bigr), \\ s_0 &= \bigl(\begin{smallmatrix}1&0\\0&-1\end{smallmatrix}\bigr), & s_1 &= \bigl(\begin{smallmatrix}0&1\\1&0\end{smallmatrix}\bigr), & s_2 &= \bigl(\begin{smallmatrix}-1&0\\0&1\end{smallmatrix}\bigr), & s_3 &= \bigl(\begin{smallmatrix}0&-1\\-1&0\end{smallmatrix}\bigr). \end{align}$

Diese Drehungen und Spiegelungen lassen sich bildlich wie folgt darstellen:

Zykel-Graph von $D_{4}$ :
ist die Drehung um 90° im Uhrzeigersinn.

ist die Spiegelung an der vertikalen Mittelachse.

$r_{0}$ (Drehung um 0°)	$r_{1}$ (Drehung um 90°)	$r_{2}$ (Drehung um 180°)	(Drehung um 270°)
$s_{0}$ (Spiegelung an der x-Achse)	$s_{1}$ (Spiegelung an der Diagonale y=x)	$s_{2}$ (Spiegelung an der y-Achse)	(Spiegelung an der Diagonale y=-x)
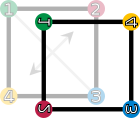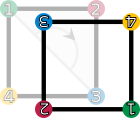
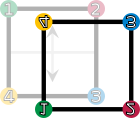
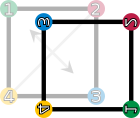
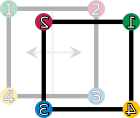
Drehungen und Spiegelungen eines Quadrates. Die vier Ecken sind nummeriert und eingefärbt, um die Transformation bildlich darzustellen.

Permutations-Darstellung

Betrachten wir zunächst als Beispiel die Diedergruppe $D_{4}$ . Diese operiert durch Symmetrietransformationen auf einem Quadrat wie in der vorangehenden Grafik gezeigt. Betrachtet man die Aktion der Diedergruppe $D_{4}$ auf den Eckpunkten $1,2,3,4$ , erhält man eine treue Darstellung in die symmetrische Gruppe $S_{4}$ , also einen injektiven Gruppenhomomorphismus $\tau \colon D_4 \to S_4$ . Genauer gesagt wirken die Transformationen auf den Ecken als folgende Permutationen:

${\begin{aligned}\tau (r_{0})&={\bigl (}{\begin{smallmatrix}1&2&3&4\\1&2&3&4\end{smallmatrix}}{\bigr )}&\tau (r_{1})&={\bigl (}{\begin{smallmatrix}1&2&3&4\\2&3&4&1\end{smallmatrix}}{\bigr )}&\tau (r_{2})&={\bigl (}{\begin{smallmatrix}1&2&3&4\\3&4&1&2\end{smallmatrix}}{\bigr )}&\tau (r_{3})&={\bigl (}{\begin{smallmatrix}1&2&3&4\\4&1&2&3\end{smallmatrix}}{\bigr )}\\\tau (s_{0})&={\bigl (}{\begin{smallmatrix}1&2&3&4\\4&3&2&1\end{smallmatrix}}{\bigr )}&\tau (s_{1})&={\bigl (}{\begin{smallmatrix}1&2&3&4\\3&2&1&4\end{smallmatrix}}{\bigr )}&\tau (s_{2})&={\bigl (}{\begin{smallmatrix}1&2&3&4\\2&1&4&3\end{smallmatrix}}{\bigr )}&\tau (s_{3})&={\bigl (}{\begin{smallmatrix}1&2&3&4\\1&4&3&2\end{smallmatrix}}{\bigr )}\end{aligned}}$

Ganz allgemein definiert die Operation der Diedergruppe $D_{n}$ auf den Eckpunkten $P_{1},P_{2},\dotsc ,P_{n}$ eine treue Darstellung $\tau \colon D_n \to S_n$ . In obiger Notation erhält man zum Beispiel die Permutation

$\tau (r_{1})=(1,2,3,\dotsc ,n).$

In Zyklenschreibweise ist dies die zyklische Permutation, die $P_{1}$ auf $P_{2}$ abbildet, $P_{2}$ auf $P_{3}$ und so weiter, bis schließlich $P_{n}$ auf $P_{1}$ abgebildet wird. Die weiteren Drehungen erhält man hieraus mittels der Relation r_k = r_1^k für alle . Für die Spiegelung an der Symmetrieachse durch $P_{n}$ erhält man entsprechend in Zyklenschreibweise

$\tau (s_{1})=(1,n-1)(2,n-2)\dots \left({\bigl \lfloor }{\tfrac {n-1}{2}}{\bigl \rfloor },{\bigl \lfloor }{\tfrac {n+2}{2}}{\bigl \rfloor }\right)$

mit der Gaußschen Ganzteilfunktion $x\mapsto \lfloor x\rfloor$ (die jeder reellen Zahl die größte ganze Zahl zuordnet, die nicht größer als ist). Die weiteren Spiegelungen erhält man hieraus mittels der Relation $s_{k+1}=r_{k}s_{1}$ für alle (mit $s_{4}=s_{0}$ ).

Erzeuger und Relationen

Alle Drehungen werden von r=r_1 erzeugt. Diese bilden eine zyklische Untergruppe der Ordnung und demnach von Index . Man erhält die gesamte Gruppe durch Hinzufügen einer beliebigen Spiegelung, zum Beispiel s = s_0 , und so die Präsentation

$D_{n}=\left\langle r,s\mid r^{n}=s^{2}=e,\ srs=r^{-1}\right\rangle ,$

wobei das neutrale Element der Gruppe ist.

Cayleygraph der Diedergruppe

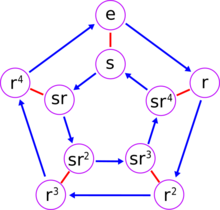
Die Verkettung von zwei Spiegelungen ist eine Drehung. Ist der Winkel zwischen den beiden Spiegelachsen $\alpha$ , so ist diese Verkettung eine Drehung um den Winkel $2\alpha$ . Das bedeutet, dass die Diedergruppe $D_{n}$ von zwei benachbarten Spiegelungen, zum Beispiel $s_{0}$ und $s_{1}$ , erzeugt wird. Man erhält so die Präsentation

$D_{n}=\left\langle s_{0},s_{1}\mid s_{0}^{2}=s_{1}^{2}=(s_{0}s_{1})^{n}=e\right\rangle .$

Dies ist der einfachste Fall einer Coxeter-Gruppe.

Für alle Indizes und gilt außerdem:

$r_{i}r_{j}=r_{i+j}$
$r_{i}s_{j}=s_{i+j}$
$s_{i}r_{j}=s_{i-j}$
$s_{i}s_{j}=r_{i-j}$

Dabei werden die Indizes jeweils modulo betrachtet ( $r_{i+n}=r_{i}$ und $s_{i+n}=s_{i}$ ).

Anwendungen

Geometrie

Diedergruppen sind die einfachsten Beispiele von Spiegelungsgruppen. Diese spielen in der klassischen Geometrie eine wichtige Rolle, zum Beispiel bei der Klassifikation der regulären Polyeder. In Dimension entsprechen hier Diedergruppen den regulären Polygonen.

Codierung

Die durch obige Permutationen definierte Zahlenverknüpfung wird bei Prüfsummenverfahren als Alternative zu diversen modulo-basierten Verfahren angewendet. Zum Beispiel besaßen die deutschen Banknoten Dieder-Prüfsummen.

Siehe auch

Unendliche Diedergruppe

Basierend auf einem Artikel in:

Wikipedia.de