S3 (Gruppe)
Die sogenannte symmetrische
Gruppe
bezeichnet im mathematischen
Teilgebiet der Gruppentheorie
eine bestimmte Gruppe
mit 6 Elementen. Sie lässt sich beschreiben als Gruppe der sechs Permutationen
einer dreielementigen Menge. Alternative Bezeichnungen sind
und
. Sie ist isomorph
mit der Diedergruppe
, der Gruppe der Kongruenzabbildungen
des gleichseitigen
Dreiecks auf sich.
Einführung
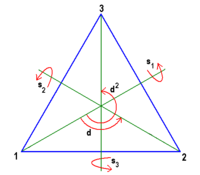
Betrachtet man die Kongruenzabbildungen, die ein gleichseitiges Dreieck in sich selbst überführen, so findet man 6 Möglichkeiten
- die identische
Abbildung
,
- die Drehung
um 120° um den Mittelpunkt des Dreiecks,
- die Drehung
um 240° um den Mittelpunkt des Dreiecks,
- drei Spiegelungen
und
an den drei Mittelsenkrechten des Dreiecks.
Diese Kongruenzabbildungen lassen sich durch Hintereinanderausführung
kombinieren, wodurch man wieder eine Kongruenzabbildung erhält. Man schreibt
einfach zwei Kongruenzabbildungen (oft ohne Verknüpfungszeichen, oder mit
)
nebeneinander und meint damit, dass
- zuerst die rechtsstehende und dann die linksstehende
Kongruenzabbildung auszuführen ist.[1] Die
Schreibweise
macht bereits deutlich, dass die Drehung um 240° gleich der zweifachen
Hintereinanderausführung der Drehung um 120° ist.
Man erhält auf diese Weise die sechselementige Gruppe
aller Kongruenzabbildungen des gleichseitigen Dreiecks auf sich. Trägt man alle
so gebildeten Verknüpfungen in eine Verknüpfungstafel
ein, so erhält man
Will man das Produkt
für zwei Elemente
aus
ausrechnen, so suche man in der Verknüpfungstafel die mit
gekennzeichnete Zeile und mit
gekennzeichnete Spalte auf; am Schnittpunkt aus dieser Zeile und dieser Spalte
steht das Produkt.
Verallgemeinert man diese Konstruktion, indem man das gleichseitige Dreieck
durch ein regelmäßiges -Eck
ersetzt, so kommt man zum Begriff der Diedergruppe.
Daher wird die hier besprochene Gruppe
auch mit
bezeichnet.
Elemente der S3 als Permutationen
Eine Kongruenzabbildung des gleichseitigen Dreiecks ist bereits dadurch
eindeutig festgelegt, wie die mit 1, 2 und 3 bezeichneten Ecken aufeinander
abgebildet werden. Jedes Element der
kann daher als Permutation
der Menge
aufgefasst werden. Sie sehen im Folgenden zuerst die Zweizeilenform
und dahinter die Zykelschreibweise
der Elemente sowie deren Ordnungen:
Eigenschaften
Keine abelsche Gruppe
Die Gruppe
ist keine abelsche
Gruppe, wie obiger Verknüpfungstafel entnommen werden kann; beispielsweise
gilt
.
Sie ist bis auf Isomorphie
die kleinste nicht-abelsche Gruppe, das heißt, jede nicht-abelsche Gruppe ist
entweder isomorph zu
oder hat mehr Elemente.
Untergruppen und Normalteiler
Die Untergruppen neben den
trivialen Untergruppen
und
selbst sind:
. Diese Untergruppe ist ein Normalteiler und wird auch als alternierende Gruppe vom Grad 3 bezeichnet.
. Diese Untergruppen sind keine Normalteiler; beispielsweise ist
.
Erzeuger und Relationen
Man kann Gruppen auch dadurch beschreiben, dass man ein Erzeugendensystem und Relationen, die die Erzeuger erfüllen müssen, angibt. Erzeuger und Relationen notiert man, durch das Zeichen | getrennt, in spitzen Klammern. Die Gruppe ist dann die von den Erzeugern erzeugte freie Gruppe modulo dem von den Relationen erzeugten Normalteiler. In diesem Sinne ist:
Irreduzible Darstellungen
Bis auf Äquivalenz hat die
drei irreduzible
Darstellungen, zwei eindimensionale und eine zweidimensionale. Zur
Angabe dieser Darstellungen genügt es, die Bilder von
und
anzugeben, denn diese Elemente erzeugen die Gruppe.
- Die triviale Darstellung:
- Die Signum-Abbildung:
- Die zweidimensionale Darstellung:
.
Zwar erhält man eine andere zweidimensionale Darstellung, wenn man
durch
ersetzt, aber diese ist äquivalent zur angegebenen. Diese Überlegungen führen zu
folgender Charaktertafel:[2]
Weitere Beispiele
Allgemeine lineare Gruppe über ℤ/2
Die allgemeine
lineare Gruppe 2-ten Grades über dem Restklassenkörper
,
ist isomorph zur .
Transformationengruppe
Die gebrochen
linearen Funktionen
mit Koeffizienten aus einem
beliebigen Körper
und den Zuordnungen[3]
erzeugen mit der Hintereinanderausführung
als Gruppenverknüpfung eine Gruppe ,
die isomorph zur
ist. Die übrigen 4 Gruppenmitglieder sind:
Die Verknüpfungstafel ist wie oben.
Die 6 Gruppenmitglieder
unterscheiden sich bei einer Einsetzung von Elementen
auch in den Wertetabellen,
wenn
wenigstens 5 Elemente hat.
Automorphismengruppe
Die
ist isomorph zur Automorphismengruppe
der kleinschen
Vierergruppe. Das ergibt sich leicht aus der Beobachtung, dass jede
Permutation der drei Elemente der Ordnung 2 der kleinschen Vierergruppe einen
Automorphismus definiert.
Anmerkungen
- ↑ Diese Reihenfolge kommt von der Operatorenperspektive, wie sie bei der Hintereinanderschaltung von Abbildungen (so auch bei den Permutationen) vorherrscht. Für die pure Gruppentheorie ist die Reihenfolge unerheblich.
- ↑ Kurt Meyberg: Algebra II. Carl Hanser Verlag (1976), ISBN 3-446-12172-2, Beispiel 9.7.1 b
- ↑
Ist
der Körper der komplexen Zahlen, genauer: die riemannsche Zahlenkugel, dann handelt es sich um Möbiustransformationen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 16.08. 2022