Cayleygraph

Der Cayleygraph der freien Gruppe mit zwei Erzeugern a und b

In der Mathematik ist ein Cayleygraph ein Graph, der die Struktur einer (meist endlich erzeugten) Gruppe beschreibt. Er hängt von einer gegebenen, normalerweise endlichen, Menge von Erzeugern der Gruppe ab.

Arthur Cayley hat 1878 als Erster Graphen benutzt, um Gruppen bildlich darzustellen; ein Ansatz, der von Max Dehn (1911), Otto Schreier (1927) und anderen weiterentwickelt wurde. Wegen Dehns großer Beiträge wurden Cayleygraphen manchmal auch (Dehnsche) Gruppenbilder genannt. Heute sind Cayleygraphen ein zentrales Werkzeug der geometrischen Gruppentheorie.

Definition

Sei eine Gruppe und ein Erzeugendensystem. Der Cayleygraph $\Gamma =\Gamma (G,S)$ ist ein gefärbter und gerichteter Graph, der wie folgt konstruiert wird:

Jedem Element von wird ein Knoten zugeordnet: Die Knotenmenge $V(\Gamma )$ von $\Gamma$ wird mit identifiziert.
Jedem Erzeuger aus wird eine Farbe $c_{s}$ zugeordnet.
Für $g\in G$ , $s\in S$ , werden die Knoten, die zu den Elementen und $gs$ gehören, mit einer gerichteten Kante der Farbe $c_{s}$ verbunden. Die Kantenmenge $E(\Gamma )$ besteht also aus Paaren der Form $(g,gs)$ , wobei $s\in S$ die Farbe bestimmt.

In der geometrischen Gruppentheorie wird meistens angenommen, dass die Menge endlich und symmetrisch sei, das heißt $S=S^{-1}$ , und das Neutralelement der Gruppe nicht enthalte. In diesem Fall ist der Cayleygraph, abgesehen von der Färbung, ein gewöhnlicher Graph: Seine Kanten sind nicht orientiert, und er enthält keine Schleifen.

Beispiele

Sei $G=\mathbb{Z }$ die unendliche zyklische Gruppe und die Menge bestehe aus dem Standarderzeuger 1 und seinem Inversen (−1 in additiver Notation). Der zugehörige Cayleygraph ist dann eine unendliche Kette.

Das Bild ist ähnlich, wenn $G=\Z/n\Z$ die endliche zyklische Gruppe von Ordnung ist und wieder aus zwei Elementen besteht, dem Standarderzeuger 1 von und seinem Inversen; dann ist der Cayleygraph der n-Zykel $C_{n}$ .

Der Cayleygraph des direkten Produkts von Gruppen ist das kartesische Produkt der jeweiligen Cayleygraphen. Der Cayleygraph der freien abelschen Gruppe $\Z^2$ mit einer Erzeugendenmenge, die aus den vier Elementen $(\pm 1,\pm 1)$ besteht, ist ein unendliches Gitter in der Ebene $\mathbb {R} ^{2}$ , während der Cayleygraph für das direkte Produkt $\mathbb {Z} /n\mathbb {Z} \times \mathbb {Z} /m\mathbb {Z}$ mit analogen Erzeugern ein endliches $n\times m$ -Gitter auf dem Torus bildet.

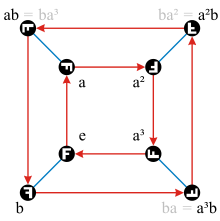
Ein Cayleygraph der Diedergruppe D₄

Anderer Cayleygraph von D₄

Der Cayleygraph der Diedergruppe D₄ mit zwei Erzeugern (90°-Drehung im Uhrzeigersinn) und (Horizontalspiegelung) ist links dargestellt. Da sein eigenes Inverses ist, sind die blauen Kanten, die für das Ausführen von stehen, ungerichtet gezeichnet. Diese Wahl von und entspricht der Präsentierung

$\langle a,b|a^{4}=b^{2}=e,ab=ba^{3}\rangle .\,$

Die Relationen der Gruppe zu dieser Wahl von Erzeugern finden sich im Cayleygraph als Zyklen wieder, zum Beispiel liefert $a^{4}$ einen geschlossenen Weg im Graphen, ebenfalls $aba^{-3}b$ .

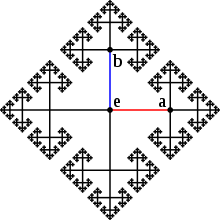
Der Cayleygraph der freien Gruppe mit zwei Erzeugern und und der Menge $S=\left\{a,b,a^{-1},b^{-1}\right\}$ ist oben im Artikel dargestellt, wobei das Neutralelement bezeichnet. Auf einer Kante nach rechts zu gehen entspricht der Rechtsmultiplikation mit , während nach oben zu gehen Multiplikation mit darstellt. Da die freie Gruppe keine Relationen besitzt, enthält dieser Graph keine Zyklen.

Charakterisierung

Die Frage, welche Graphen als Cayleygraphen einer Gruppe auftreten können, lässt sich wie folgt beantworten: Die Gruppe wirkt durch Linksmultiplikation auf sich selbst (siehe auch Satz von Cayley). Diese Wirkung liefert auch eine Wirkung von auf seinem Cayleygraphen. Konkret schickt ein Element $h\in G$ einen Knoten $g\in V(\Gamma )$ auf den Knoten $hg\in V(\Gamma )$ . Die Kantenmenge des Graphen wird durch diese Wirkung respektiert, denn eine Kante $(g,gs)$ wird auf die Kante $(hg,hgs)$ abgebildet. Die Wirkung der Linksmultiplikation irgendeiner Gruppe auf sich selbst ist einfach transitiv. Dementsprechend ist ein Cayleygraph knotentransitiv. Dies führt zu der folgenden Charakterisierung von Cayleygraphen:

Ein Graph $\Gamma$ ist ein Cayleygraph einer Gruppe genau dann, wenn er eine auf den Knoten einfach transitive Wirkung von durch Automorphismen des Graphen (also die Kantenmenge respektierende Abbildungen) zulässt.

Um die Färbung des Graphen durch die Gruppe und die Erzeugermenge zu rekonstruieren, wählt man einen Knoten $v_{1}\in V(\Gamma )$ aus und beschriftet ihn mit dem Neutralelement der Gruppe. Jeder Knoten von $\Gamma$ wird dann mit dem eindeutigen Element von bezeichnet, das $v_{1}$ nach abbildet. Die Menge von Erzeugern von , die $\Gamma$ als Cayleygraphen liefert, ist dann die Menge der Beschriftungen der Knoten, die zum ausgewählten Knoten $v_{1}$ adjazent sind. Die Erzeugermenge ist genau dann endlich, wenn der Graph lokal endlich ist, also jeder Knoten zu endlich vielen Kanten adjazent ist.

Es ist allerdings nicht wahr, dass jeder knotentransitive Graph als Cayleygraph auftritt, und auch sonst beantwortet die obige Aussage natürlich nicht alle Fragen zur Struktur von Cayleygraphen. Beispielsweise ist die Vermutung, dass jeder endliche Cayleygraph einen Hamiltonkreis enthält, bekannt als Lovász-Vermutung, unbewiesen.

Einfache Eigenschaften

Der Cayleygraph Γ(G,S) hängt wesentlich von der Wahl der Erzeugermenge S ab. Wenn S zum Beispiel k Elemente hat, so besitzt jeder Knoten von Γ k eingehende und k ausgehende Kanten. Ist S symmetrisch gewählt, so ist Γ ein regulärer Graph von Grad k.

Zyklen, das heißt geschlossene Wege, im Cayleygraphen stellen Relationen (siehe Präsentierung einer Gruppe) zwischen den Elementen von S dar.

Wenn $f\colon G'\to G$ ein surjektiver Gruppenhomomorphismus ist, der auf der Erzeugermenge S’ von G’ injektiv ist, dann induziert f eine Überlagerung von Graphen

${\bar {f}}\colon \Gamma (G',S')\to \Gamma (G,S),\quad$ wobei S = f(S’).

Insbesondere ist dies der Fall, wenn eine Gruppe G von k Elementen erzeugt wird, alle von Ordnung ungleich 2, und die Menge S aus diesen Erzeugern und ihren Inversen besteht. Dann wird der Cayleygraph Γ(G,S) vom unendlichen regulären Baum von Grad 2k überlagert, der zur freien Gruppe über denselben Erzeugern gehört. Ein solcher Baum ist dann eine universelle Überlagerung des Cayleygraphen und heißt auch Cayleybaum oder Bethe-Gitter.

Auch wenn die Menge S die Gruppe G nicht erzeugt, kann ein Graph Γ(G,S) konstruiert werden. Allerdings wird er nicht zusammenhängend sein und wird nicht als Cayleygraph betrachtet. In diesem Fall entspricht jede Zusammenhangskomponente einer Nebenklasse der Untergruppe, die von S erzeugt wird.

Anwendungen in der Gruppentheorie

Durch das Studium des Cayleygraphen können Einsichten über die Struktur der Gruppe gewonnen werden. Unter anderem ist es interessant, die Adjazenzmatrix zu untersuchen, insbesondere mit den Mitteln der Spektraltheorie von Graphen, die geometrische Aussagen, die aus dem Spektrum von linearen Operatoren gewonnen werden, in einen diskreten Kontext überträgt.

Geometrische Gruppentheorie

Für unendliche Gruppen ist die grobe Geometrie (coarse geometry) des Cayleygraphen, oder seine Äquivalenzklasse bis auf Quasi-Isometrie, fundamental für das Gebiet der geometrischen Gruppentheorie. Für eine endlich erzeugte Gruppe ist sie unabhängig von der Wahl einer endlichen Menge von Erzeugern, also eine intrinsische Eigenschaft der Gruppe. Dies ist nur für unendliche Gruppen interessant, da alle endlichen Gruppen – für die $S=G$ gewählt werden kann – quasiisometrisch zu einem Punkt sind.

Der Cayleygraph ist in diesem Zusammenhang ein metrisches Bild der Gruppe zusammen mit der Wortmetrik, die durch die Wahl der Erzeuger bestimmt wird.

Wortmetrik

Die Wortmetrik auf dem Cayleygraphen ist gegeben durch die Festlegung, dass alle Kanten des Graphen Länge 1 haben sollen. Äquivalent kann man den Abstand zweier Gruppenelemente g,h definieren als die minimale Anzahl von Faktoren aus dem gegebenen Erzeugendensystem, in die sich $gh^{{-1}}$ zerlegen lässt, also

$d(g,h)=\min\{n:gh^{-1}=s_{1}\dots s_{n};s_{1},\dots ,s_{n}\in S\}$ .

Die Wortmetrik hängt (ebenso wie der Cayleygraph selbst) vom Erzeugendensystem ab. Für verschiedene endliche Erzeugendensysteme erhält man aber quasi-isometrische (sogar bilipschitz-äquivalente) Cayleygraphen. Alle bis auf Quasi-Isometrie bestimmten geometrischen Eigenschaften von Graphen entsprechen also Eigenschaften von Gruppen.

In der geometrischen Gruppentheorie versucht man, algebraische Eigenschaften von Gruppen in geometrische Eigenschaften des Cayleygraphen zu übersetzen. Ein spektakuläres Beispiel dafür ist Gromows Satz, dass eine Gruppe genau dann virtuell nilpotent ist, wenn ihr Cayleygraph polynomielles Volumenwachstum hat, d.h. das Volumen der Bälle vom Radius durch ein Polynom in nach oben begrenzt ist.

Wort-hyperbolische Gruppen

Eine Gruppe heißt wort-hyperbolisch, wenn ihr Cayleygraph δ-hyperbolisch für ein $\delta >0$ ist. Das bedeutet, dass in jedem geodätischen Dreieck jeder auf einer Kante liegende Punkt Abstand $<\delta$ von mindestens einer der beiden anderen Kanten hat. Diese Definition ist (bis auf den genauen Wert der Konstante $\delta$ ) invariant unter Quasi-Isometrie und deshalb unabhängig vom gewählten Erzeugendensystem.

Beispiele wort-hyperbolischer Gruppen sind: endliche Gruppen, virtuell zyklische Gruppen, endlich erzeugte freie Gruppen, Fundamentalgruppen kompakter --Flächen negativer Euler-Charakteristik und allgemein Fundamentalgruppen kompakter, negativ gekrümmter Mannigfaltigkeiten. In gewisser Weise sind zufällige Gruppen wort-hyperbolisch.

Rand im Unendlichen

Der Cayleygraph hat einen Rand im Unendlichen, formal definiert als die Menge der Äquivalenzklassen geodätischer Strahlen, wobei 2 Strahlen genau dann äquivalent sind, wenn sie endlichen Abstand haben. Die Wirkung der Gruppe auf dem Rand im Unendlichen ist ein „chaotisches“ dynamisches System und kodiert viele Eigenschaften der Gruppe.

Beispiele: für freie Gruppen ist der Rand im Unendlichen eine Cantor-Menge, für Fundamentalgruppen kompakter negativ gekrümmter -Mannigfaltigkeiten ist der Rand im Unendlichen eine (n-1) -Sphäre, für die „meisten“ wort-hyperbolischen Gruppen ist der Rand im Unendlichen aber ein Menger-Schwamm.

Geschichte

Cayley betrachtete die nach ihm benannten Graphen 1878 zunächst nur für endliche Gruppen. In seinen unveröffentlichten Notizen zur Gruppentheorie aus den Jahren 1909–10 führte Max Dehn den Cayleygraphen unter dem Namen „Gruppenbild“ ein. Seine Hauptanwendung war die Lösung des Wortproblems für die Fundamentalgruppen der Flächen vom Geschlecht ≥ 2 mit geometrischen Methoden, die heute zur Theorie der hyperbolischen Gruppen gehören. (Das ist äquivalent zur Lösung des topologischen Problems, welche Kurven in der Fläche sich auf einen Punkt zusammenziehen lassen.) Diese Arbeit war der Beginn der heutigen geometrischen Gruppentheorie.