Hyperbolische Gruppe

Hyperbolische Gruppen (auch: wort-hyperbolische Gruppen, Gromov-hyperbolische Gruppen, negativ gekrümmte Gruppen) sind eines der zentralen Themen der geometrischen Gruppentheorie.

Der Begriff wurde in den 1980er Jahren von Michail Leonidowitsch Gromow eingeführt, die Verwendung geometrischer Methoden in der Gruppentheorie hat aber eine lange bis zu Max Dehns Verwendung hyperbolischer Geometrie zur Lösung des Wortproblems für Fundamentalgruppen kompakter Flächen zurückreichende Tradition. In gewissem Sinne sind fast alle Gruppen hyperbolisch. Zahlreiche Methoden aus der Geometrie negativ gekrümmter Räume lassen sich auf hyperbolische Gruppen übertragen und so für die Gruppentheorie nutzbar machen.

Definition

Eine endlich erzeugte Gruppe ist hyperbolisch, wenn der einem endlichen Erzeugendensystem zugeordnete Cayley-Graph $\delta$ -hyperbolisch für ein $\delta >0$ ist. Diese Definition ist unabhängig von der Wahl des endlichen Erzeugendensystems.

Ausführlicher:

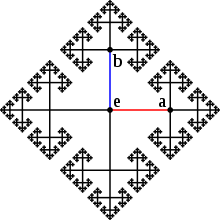
Der Cayleygraph der freien Gruppe mit zwei Erzeugern und

Der zu einem endlichen Erzeugendensystem S einer Gruppe G zugeordnete Cayley-Graph ist der wie folgt definierte Graph (V,E) : Die Knotenmenge ist die Gruppe , die Kantenmenge besteht aus Paaren der Form $(g,gs)$ , wobei ein beliebiges Gruppenelement und ein Element aus $S\cup S^{-1}$ ist. Das Bild rechts zeigt den Cayley-Graphen der von zwei Elementen $S=\left\{a,b\right\}$ erzeugten freien Gruppe.

Durch die Festlegung, dass alle Kanten Länge haben, wird der Cayley-Graph zu einem metrischen Raum. (Die induzierte Metrik auf der Knotenmenge heißt die Wort-Metrik der Gruppe .)

Für verschiedene endliche Erzeugendensysteme erhält man quasi-isometrische Cayleygraphen. Alle bis auf Quasi-Isometrie bestimmten geometrischen Eigenschaften von Graphen entsprechen also Eigenschaften von Gruppen.

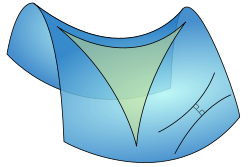
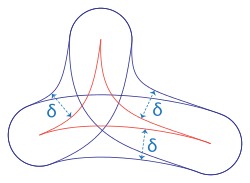
Ein geodätisches Dreieck in einer negativ gekrümmten Fläche

Ein δ-dünnes Dreieck

Ein metrischer Raum heißt $\delta$ -hyperbolisch für ein $\delta >0$ wenn alle geodätischen Dreiecke δ-dünn sind, d.h. jede Kante des Dreiecks in der $\delta$ -Umgebung der Vereinigung der beiden anderen Kanten enthalten ist:

$[x,y]\subseteq B_{\delta }([y,z]\cup [z,x]),$

$[y,z]\subseteq B_{\delta }([z,x]\cup [x,y]),$

$[z,x]\subseteq B_{\delta }([x,y]\cup [y,z]).$

Diese Bedingung ist zum Beispiel für geodätische Dreiecke in Bäumen mit $\delta =0$ oder in der hyperbolischen Ebene mit $\delta =\ln \left({\sqrt {2}}+1\right)$ erfüllt, allgemeiner für geodätische Dreiecke in einfach zusammenhängenden Riemannschen Mannigfaltigkeiten negativer Schnittkrümmung. Im Euklidischen Raum ist die Eigenschaft dagegen nicht erfüllt: für jedes $\delta >0$ kann man in einem Dreieck durch einfache Skalierung mit einem konstanten positiven, von $\delta$ abhängigen Faktor zu einem Dreieck gelangen, bei dem die $\delta$ -Umgebung von zwei Kanten nicht die $\delta$ -Umgebung der dritten Kante im Dreieck umfasst.

Wenn zwei metrische Räume $(X_{1},d_{1})$ und $(X_{2},d_{2})$ quasi-isometrisch sind, dann ist $(X_{1},d_{1})$ $\delta$ -hyperbolisch für ein $\delta >0$ genau dann, wenn $(X_{2},d_{2})$ $\delta ^{\prime }$ -hyperbolisch für ein (eventuell verschiedenes) $\delta ^{\prime }>0$ ist. Insbesondere ist der einem endlichen Erzeugendensystem zugeordnete Cayley-Graph einer Gruppe $\delta$ -hyperbolisch für ein $\delta >0$ genau dann, wenn dies für jedes endliche Erzeugendensystem zutrifft.

Damit kann man dann unabhängig vom gewählten endlichen Erzeugendensystem einer Gruppe definieren: die Gruppe ist hyperbolisch, wenn der Cayley-Graph $\delta$ -hyperbolisch für ein $\delta >0$ ist.

Beispiele

Endliche Gruppen und virtuell zyklische Gruppen sind hyperbolisch, diese Gruppen werden oft als elementare hyperbolische Gruppen bezeichnet.
Endlich erzeugte freie Gruppen sind hyperbolisch.
Fundamentalgruppen kompakter Riemannscher Mannigfaltigkeiten negativer Schnittkrümmung sind hyperbolisch. Das umfasst insbesondere Fundamentalgruppen kompakter hyperbolischer Mannigfaltigkeiten, zum Beispiel Fundamentalgruppen von kompakten Flächen negativer Euler-Charakteristik.
Eine „zufällig gewählte“ Gruppe ist hyperbolisch. Das heißt genauer: Für eine (beliebig, aber fest gewählte) natürliche Zahl und ein $d\in \mathbb {R}$ mit $1/2<d<1$ betrachte man zu jeder natürlichen Zahl alle Gruppen mit Erzeugern und (höchstens) $dL$ Relationen der Länge (höchstens) . Sei $P(n,d,L)$ der Anteil der hyperbolischen Gruppen in dieser Menge von Gruppen. Gromov hat bewiesen, dass für gegen unendlich der Anteil $P(n,d,L)$ gegen 100 % geht.
Eine Gruppe, die $\mathbb {Z} \oplus \mathbb {Z}$ als Untergruppe enthält, ist nicht hyperbolisch.

Anwendungen

Verschiedene für beliebige Gruppen formulierbare (und im Allgemeinen offene) Vermutungen wurden für die Klasse der hyperbolischen Gruppen unter Benutzung deren spezieller Geometrie bewiesen. Dazu gehören:

die Novikov-Vermutung
die Baum-Connes-Vermutung
die Farrell-Jones-Vermutung

Rand im Unendlichen

$\delta$ -hyperbolische Räume haben einen meist als Gromov-Rand bezeichneten Rand im Unendlichen $\partial X$ . Dieser ist definiert als die Menge der Äquivalenzklassen geodätischer Strahlen, wobei zwei Strahlen genau dann äquivalent sind, wenn sie endlichen Abstand haben.

Nach Wahl eines festen Basispunktes $x\in X$ definiert man die Topologie von $\partial X$ wie folgt: Als Umgebungsbasis eines Punktes $p\in \partial X$ verwendet man alle $V(p,r)\subset \partial X$ mit $r\geq 0$ , wobei $V(p,r)$ die Menge aller $q\in \partial X$ ist, so dass und durch von ausgehende geodätische Strahlen $\gamma _{1},\gamma _{2}$ repräsentiert werden, für die $\liminf _{t\rightarrow \infty }(\gamma _{1}(t),\gamma _{2}(t))_{x}\geq r$ ist. Hier bezeichnet $(.,.)_{x}$ das Gromov-Produkt $(y,z)_{x}={\frac {1}{2}}(d(x,y)+d(x,z)-d(y,z))$ . Die Topologie auf $\partial X$ ist unabhängig vom gewählten .

Quasi-isometrische Räume haben homöomorphe Ränder im Unendlichen. Insbesondere ist der Rand einer hyperbolischen Gruppe wohldefiniert (unabhängig vom Erzeugendensystem ) als Rand im Unendlichen des Cayley-Graphen. Beispiele: für freie Gruppen ist der Rand im Unendlichen eine Cantormenge, für Fundamentalgruppen kompakter -dimensionaler Riemannscher Mannigfaltigkeiten mit negativer Schnittkrümmung ist der Rand im Unendlichen eine (n-1) -dimensionale Sphäre, für die „meisten“ hyperbolischen Gruppen ist der Rand im Unendlichen ein Menger-Schwamm.

Quasi-Isometrien, insbesondere Isometrien, eines $\delta$ -hyperbolischen Raumes wirken als Homöomorphismen auf $\partial X$ . Insbesondere wirkt jede hyperbolische Gruppe durch Isometrien auf ihrem Cayley-Graphen und damit durch Homöomorphismen auf dessen Rand im Unendlichen. Die Wirkung der hyperbolischen Gruppe auf dem Rand im Unendlichen ist ein „chaotisches“ dynamisches System.

Eine hyperbolische Gruppe wirkt als Konvergenzgruppe auf ihrem Rand im Unendlichen und dies erlaubt eine topologische Charakterisierung hyperbolischer Gruppen: Eine Gruppe ist genau dann hyperbolisch, wenn sie als gleichmäßige Konvergenzgruppe auf einem perfekten, kompakten, metrisierbaren Raum wirkt.

Basierend auf einem Artikel in:

Wikipedia.de