Ikosaeder

Regelmäßiges Ikosaeder

Art der Seitenflächen	gleichseitige Dreiecke
Anzahl der Flächen	20
Anzahl der Ecken	12
Anzahl der Kanten	30
Schläfli-Symbol	{3,5}
dual zu	Pentagondodekaeder
Netz
Anzahl verschiedener Netze	43380
Anzahl Kanten in einer Ecke	5
Anzahl Ecken einer Fläche	3

Das (auch, v.a. österr.: der) Ikosaeder [ikozaˈeːdər] (von altgriechisch εἰκοσάεδρον eikosáedron „Zwanzigflach“) ist ein Polyeder (ein Vielflächner), genauer: einer der fünf platonischen Körper, mit:

zwanzig (kongruenten) gleichseitigen Dreiecken als Flächen
dreißig (gleich langen) Kanten und
zwölf Ecken, in denen jeweils fünf Flächen zusammentreffen.

Symmetrie

Wegen seiner hohen Symmetrie – alle Ecken, Kanten und Flächen sind untereinander gleichartig – ist das Ikosaeder ein reguläres Polyeder. Es hat:

sechs fünfzählige Drehachsen (durch gegenüberliegende Ecken)
zehn dreizählige Drehachsen (durch die Mittelpunkte gegenüberliegender Flächen)
fünfzehn zweizählige Drehachsen (durch die Mittelpunkte gegenüberliegender Kanten)
fünfzehn Symmetrieebenen (durch einander gegenüberliegende – und parallele – Kanten)

und ist

zentralsymmetrisch (Punktspiegelung am Mittelpunkt des Polyeders).

Insgesamt hat die Symmetriegruppe des Ikosaeders – die Ikosaeder- oder Dodekaedergruppe – 120 Elemente (Ikosaedergruppe). Die Untergruppe der Drehungen des Ikosaeders hat die Ordnung 60 und ist die kleinste nichtabelsche einfache Gruppe (A5, Alternierende Gruppe der Ordnung 5). Die Symmetrie des Ikosaeders ist (wegen der bei ihm auftretenden fünfzähligen Symmetrie) mit einer periodischen Raumstruktur nicht verträglich. Es kann daher kein Kristallgitter mit Ikosaedersymmetrie geben (vgl. jedoch Quasikristalle).

Kartesische Koordinaten

Die folgenden Kartesischen Koordinaten definieren die Ecken eines Ikosaeders mit Kantenlänge a = 2, zentriert am Ursprung:

(0, ±1, ± $\varphi$ )

(±1, ± $\varphi$ , 0)

(± $\varphi$ , 0, ±1)

mit $\varphi ={\tfrac {1}{2}}(1+{\sqrt {5}})$ (Goldene Zahl).

Beziehungen zu anderen Polyedern

Ikosaeder (grün) und sein dualer Körper, das Pentagondodekaeder (gelb).

Fußball – Wabenstruktur aus Fünf- und Sechsecken

Das Pentagondodekaeder ist das zum Ikosaeder duale Polyeder (und umgekehrt).
Mit Hilfe von Ikosaeder und Dodekaeder können zahlreiche Körper konstruiert werden, die ebenfalls die Ikosaedergruppe als Symmetriegruppe haben. So erhält man zum Beispiel

ein abgestumpftes Ikosaeder mit 20 Sechsecken und 12 Fünfecken, ähnlich einem Fußball (siehe unten), siehe auch Fulleren. Es entsteht aus dem Ikosaeder, indem die Ecken so gekappt werden, dass stets ein regelmäßiges Fünfeck als Schnittfläche auftritt.

ein Ikosidodekaeder mit 20 Dreiecken und 12 Fünfecken
ein abgestumpftes Dodekaeder mit 20 Dreiecken und 12 Zehnecken als Durchschnitte eines Ikosaeders mit einem Dodekaeder (siehe archimedische Körper)
ein Rhombentriakontaeder mit 20 + 12 = 32 Ecken und 30 Rhomben als Flächen als konvexe Hülle einer Vereinigung eines Ikosaeders mit einem Dodekaeder und
einen Ikosaederstern, indem sämtliche Kanten eines Ikosaeders über seine Ecken hinaus verlängert werden, bis sich jeweils drei von ihnen in einem Punkt schneiden.

Zur Struktur des Ikosaeders

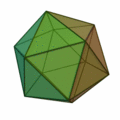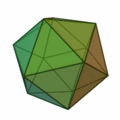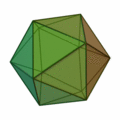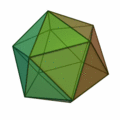
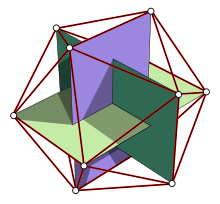
Wie die untenstehende Graphik zeigt, kann man unter den Kanten des Ikosaeders drei Paare gegenüber liegender (also insgesamt sechs) Kanten so auswählen, dass diese Paare drei kongruente zueinander paarweise orthogonale Rechtecke aufspannen. (Die Längen der Seiten dieser Rechtecke entsprechen dem Goldenen Schnitt, weil sie Seiten bzw. Diagonalen regelmäßiger Fünfecke sind.) Das Ikosaeder kann daher so in einen Würfel eingeschrieben werden, dass diese sechs Kanten in den sechs Flächen des Würfels liegen und parallel zu den Kanten des Würfels sind.

Die 24 restlichen Kanten begrenzen 8 Dreiecke (unter den 20 Flächen des Ikosaeders), die in den Flächen eines – dem Ikosaeder umschriebenen – Oktaeders liegen, wobei die Ecken des Ikosaeders auf dessen Kanten liegen.

Insgesamt gibt es fünf derartige Positionen, wobei jede Kante des Ikosaeders zu genau einer solchen Gruppe von orthogonalen Kantenpaaren gehört, während jede Fläche zweimal in der Fläche eines umschriebenen Oktaeders liegt. Die Symmetriegruppe des Ikosaeders bewirkt alle 5!/2 = 60 geraden Permutationen dieser fünf Positionen.

Die Kanten des Ikosaeders enthalten zwölf ebene Fünfecke, wobei jede Kante zu zwei und jede Ecke zu fünf dieser Fünfecke gehört. Man kann diese Eigenschaft zum Bau eines Drahtmodells benutzen.

Formeln

Größen eines Ikosaeders mit Kantenlänge a
Volumen	$V={\frac {5}{12}}a^{3}\left(3+{\sqrt {5}}\right)$
Oberflächeninhalt	$A_{O}=5a^{2}{\sqrt {3}}\,=V\,'(\rho )$
Umkugelradius	$R={\frac {a}{4}}{\sqrt {10+2{\sqrt {5}}}}$
Kantenkugelradius	$r={\frac {a}{4}}\left(1+{\sqrt {5}}\right)$
Inkugelradius	$\rho ={\frac {a}{12}}{\sqrt {3}}\left(3+{\sqrt {5}}\right)$
Verhältnis von Volumen zu Umkugelvolumen	${\frac {V}{V_{{UK}}}}={\frac {{\sqrt {10+2{\sqrt {5}}}}}{2\pi }}$
Flächenwinkel ≈ 138° 11′ 23″	$\cos \,\alpha =-{\frac {1}{3}}{\sqrt {5}}$
3D-Kantenwinkel = 108°	$\cos \,\gamma ={\frac {1}{4}}\left(1-{\sqrt {5}}\right)$
Eckenraumwinkel ≈ 0,8386 π	$\cos \,\Omega =-{\frac {95}{243}}{\sqrt {5}}$

Bedeutung des Ikosaeders in der Clusterphysik

Große Bedeutung hat die Ikosaeder-Form bei Clustern (Ansammlungen von Atomen in der Größenordnung von 3 bis 50.000 Atomen) ab einer Größe von mehr als 7 Atomen. Grund dafür ist die Regel von Friedel, die besagt, dass diejenige Struktur die geringste Energie besitzt, für die die Anzahl der Nächste-Nachbarn-Bindungen maximal ist. Bei vielen freien Clustern tritt dies ab 7 Atomen auf, wobei es allerdings auch Ausnahmen gibt und andere Strukturen bevorzugt werden (etwa Kuben).

Des Weiteren gibt es in der Clusterphysik sogenannte magische Zahlen, die eng mit dem sogenannten Mackayschen Ikosaeder zusammenhängen. Hier sorgen Schalenabschlüsse (also perfekte Atom-Ikosaeder) für besonders stabile Cluster. Dies tritt bei Clustern mit den magischen Atomzahlen 1, 13, 55, 147, 309, 561, 923 und 1415 auf. Diese recht alten Erkenntnisse von Alan Mackay spielen in der aktuellen Clusterphysik eine bedeutende Rolle.

Die Clusterzahlen lassen sich nach folgender Formel berechnen:

$C=\,{\frac {10n^{3}-15n^{2}+11n-3}{3}}$

C = Gesamtzahl der Atome im Cluster
n = Anzahl der Atome pro Kante

Anwendungen

Zwanzigseitiger Spielwürfel

Die Capside vieler Viren haben eine ikosaedrische Symmetrie. Das ist dadurch zu erklären, dass Viren ihre Nukleinsäure optimal verpacken. Die Ikosaederform ist in dieser Hinsicht günstig, weil das Ikosaeder von allen regelmäßigen Polyedern mit gegebenem Durchmesser das größte Volumen besitzt.
Rudolf von Laban hatte das Ikosaeder für seine Raumharmonielehre intensiv genutzt und beeinflusste damit den modernen Tanz. Dies wird heute in den Laban-Bewegungsstudien weiter geführt.
Stafford Beer hatte in seiner kybernetischen Managementtheorie die Ikosaeder-Struktur als Modell für eine optimale Vernetzung von Mitarbeitern in Teams herausgearbeitet.
In vielen Rollenspielen werden Ikosaeder als zwanzigseitige Spielwürfel (W20) verwendet.
Ein in die Erdkugel platziertes Ikosaeder bildet den Kern der Gitterstruktur beim Wettervorhersagemodell ICON des Deutschen Wetterdienstes.
Der Dogic ist eine Variante des Zauberwürfels in Form eines Ikosaeders als dreidimensionales, mechanisches Puzzle.
Im Inneren eines Magic 8 Ball befindet sich ein Ikosaeder, auf dem die möglichen Antworten stehen. Es schwimmt in einer dunkelblauen Flüssigkeit im Inneren der Kugel.

Basierend auf einem Artikel in:

Wikipedia.de